в конечном итоге сводится к решению простейших тригонометрических уравнений. И
в этом наилучшим помощником снова оказывается тригонометрический круг.Вспомним определения косинуса и синуса.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



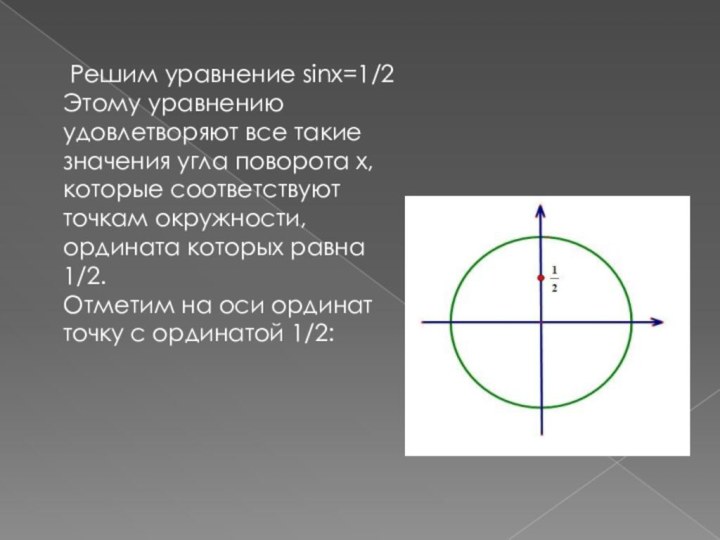
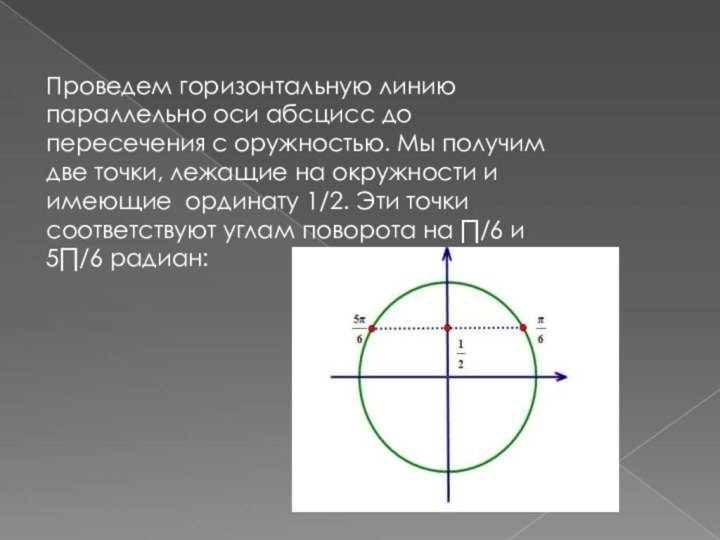


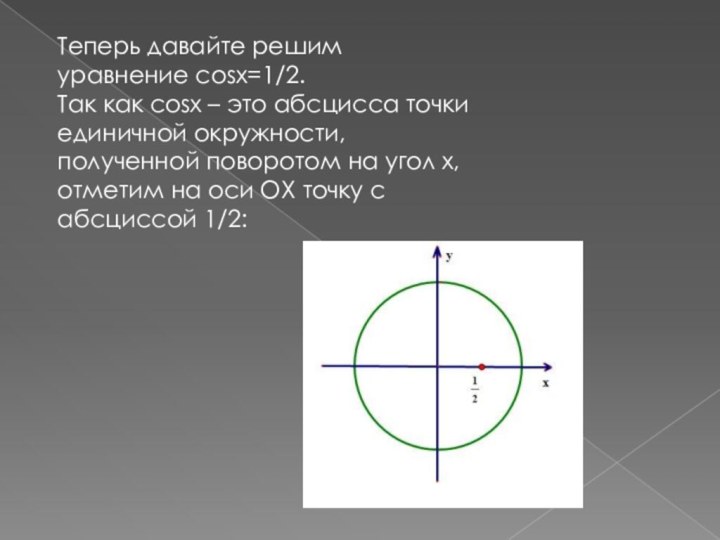


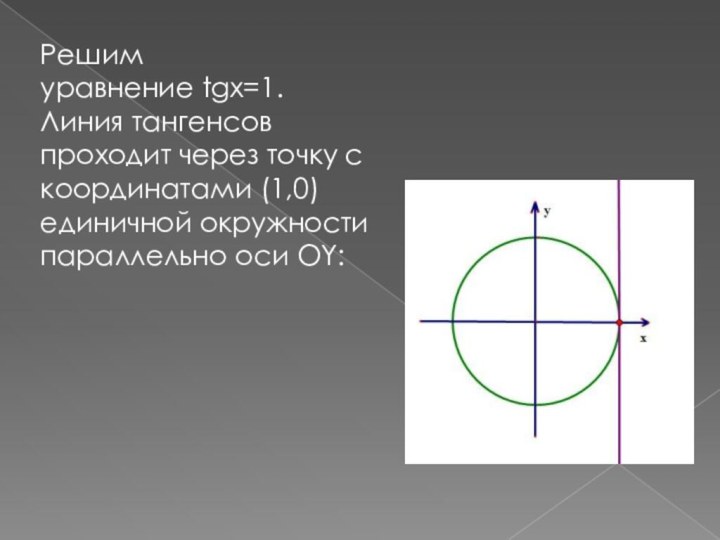





То есть первая серия решений исходного уравнения имеет вид:
X1=∏/6+2∏k, где k Z, Z – множество целых чисел
вторая серия решений имеет вид:
x2=5∏/6+2∏k
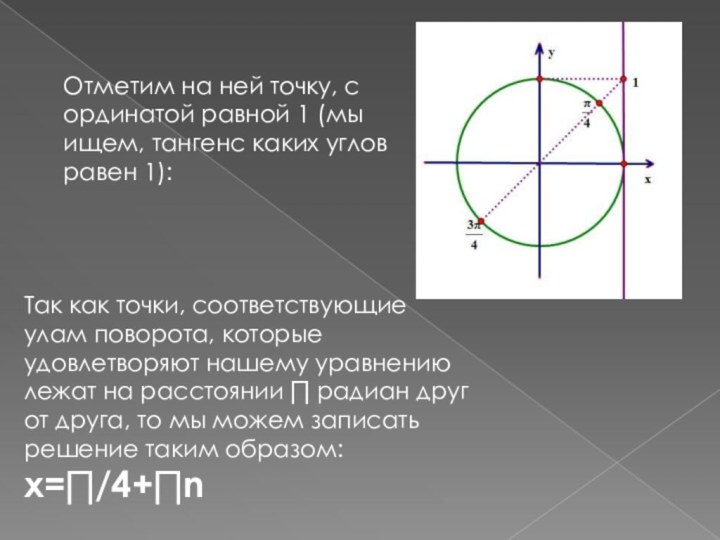
Поскольку эти точки отстоят друг от друга на расстояние, равное ∏, то общее решение этого уравнения мы можем записать так:
x=3∏/4+∏n