-А нигде! До вчерашнего дня стояли они у меня
на берегу друг за дружкой, по росту. А нынче ночью надумал я бежать. Надоели мне эти приказы-капризы хуже горькой редьки! Ну, сложил я все шарики и кубики по порядку один в другой, и - бултых в воду...
- Не может быть! -в один голос закричали мы с Пи.- Неужто мы так и не увидим вашей работы?!
- Кто его знает! - уклончиво хмыкнул матрос.- Коли очень захотите, может, и увидите. Не наяву, так в уме... - Вы хотите сказать, в воображении? - уточнил я.
- Вот-вот,- обрадованно закивал матрос.- С воображением да с соображением чего не увидишь!
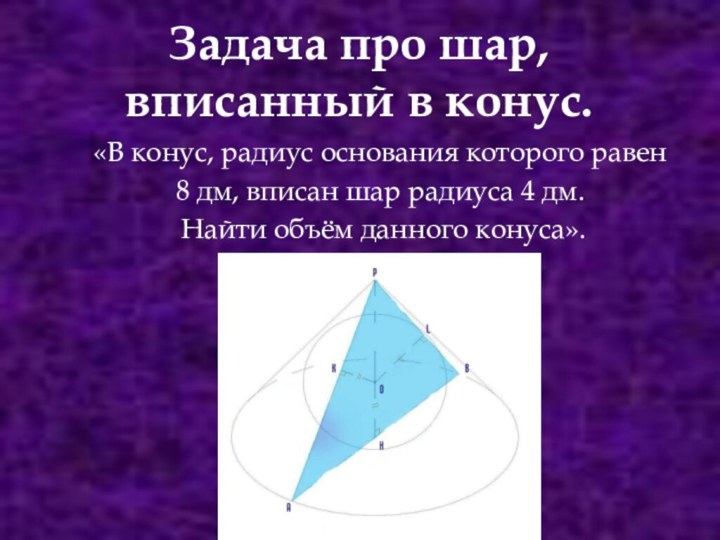
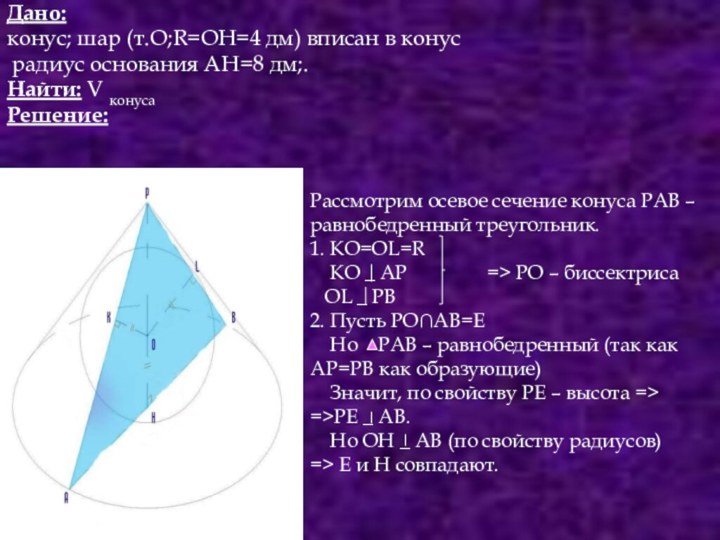
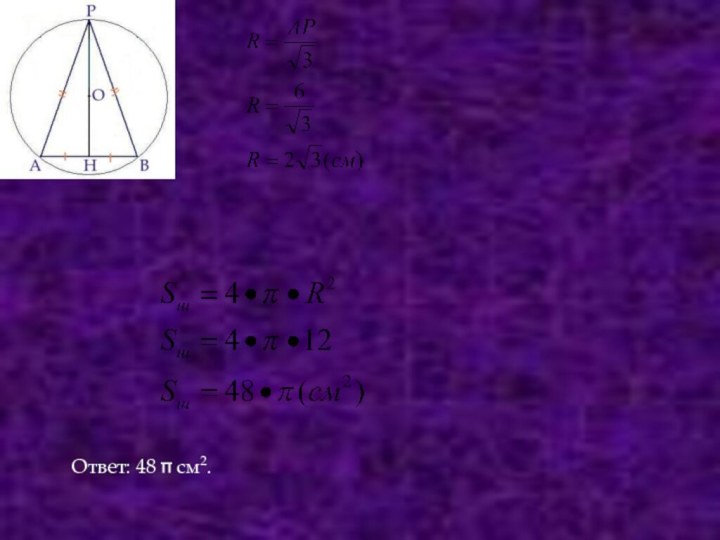
- Ваша правда,- подтвердил капитан.- Но вы забыли про знания. Чтобы вообразить себе что-нибудь как следует -ну хоть ваши кубики и шарики, необходимо кое-что
смыслить в геометрии. Надо, например, знать, что, с точки зрения геометрии, шар только тогда считается вписанным в куб по-настоящему, когда поверхность его касается всех шести граней куба, иначе говоря, имеет с ним шесть точек касания.
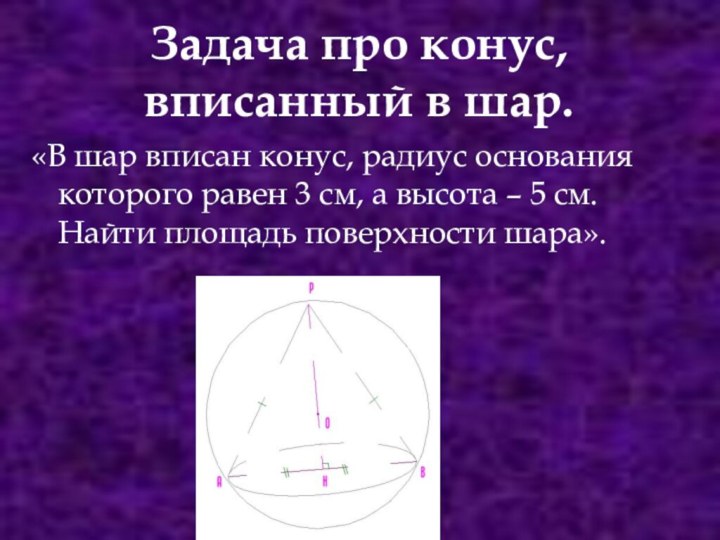
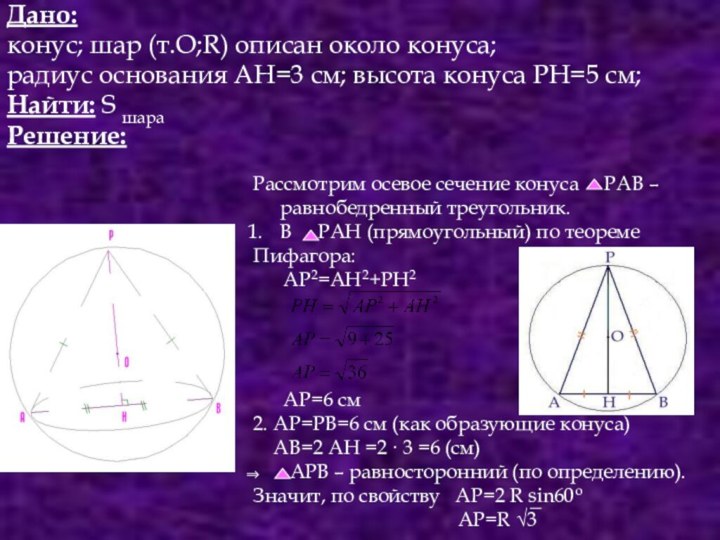
Если же речь идёт о шаре, описанном вокруг, или, как говорят математики, около куба, значит, подразумевается, что поверхность его непременно проходит через все восемь вершин куба.
- Э, нет,- не согласился я,- раз шар описан около куба, стало быть, куб у него внутри. Но тогда с вершинами куба соприкасается не поверхность шара, а его внутренность...