Презентация, доклад по математике на тему: Задачи на вычисление объемов и площадей поверхностей тел вращения

Задачи на вычисление объемов и площадей поверхности тел вращения.

( урок подготовки к сдаче ЕГЭ по математике базового уровня в 12 классах вечерней школы)

Медведева Ю. Л.
г. Новый Уренгой
2017 г.

Повторение:

:

Устно: 1. У Васи 10 яблок, а у Пети 2 яблока. Во сколько раз у Васи яблок больше, чем у Пети?

2. У Васи 10 яблок, а у Пети 2 яблока. Во сколько раз у Пети яблок меньше, чем у Васи?

Вывод 1 : Чтобы узнать, во сколько раз одна величина больше (или меньше) другой, нужно значение большей величины разделить на значение меньшей.

Вывод 2 : В задаче при необходимости можно заменять условие «в… больше» на «в … меньше», и наоборот.

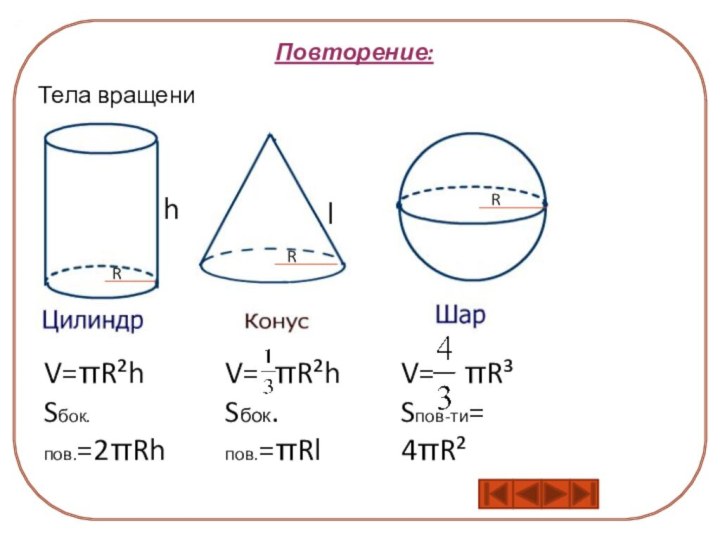
Решая задачи на тела вращения, в которых сравнивают 2 величины, ни одна из которых неизвестна, меньшую договоримся принимать равной единице, а условие «в … мешьше» всегда заменять на «в … больше».

Повторение:

Пропорция – верное равенство двух отношений.

Основное свойство пропорции:  Произведение крайних членов пропорции равно произведению ее средних членов.

:

;

.

;

;

?

Повторение:

:

Найти значение переменной используя основное свойство пропорции:

,

,

.

.

Повторение:

:

Тела вращения:

V=πR²h
Sбок.пов.=2πRh

h

V= πR²h
Sбок.пов.=πRl

l

V= πR³
Sпов-ти= 4πR²

R

R

R

:

Алгоритм:


Прочитать задание, особое внимание уделить вопросу задачи.
Выписать нужную формулу.
Составить и заполнить таблицу.
Выполнить решение.

:

Задача 1: Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9 , а второго – 9 и 2. Во сколько раз объем первого цилиндра больше объема второго?

Читаем вопрос задачи. Выписываем формулу для вычисления объема цилиндра.
V=πR²h
Составляем и заполняем таблицу.
«Собираем» формулу.

Π 6² 9

Π 9² 2

=

2

Ответ: 2

:

Задача 2: Даны два шара с радиусами 7 и 1. Во сколько раз объем большего шара больше объема другого?

Читаем вопрос задачи. Выписываем формулу для вычисления объема шара
V= πR³
Составляем и заполняем таблицу:
«Собираем» формулу:

Ответ: 343

:

Задача 3: Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5, а второго 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого конуса?

Читаем вопрос задачи. Выписываем формулу для вычисления площади боковой поверхности конуса
Sбок.= πRl
Составляем и заполняем таблицу
«Собираем» формулу

Ответ: 3

:

Задача 4: Даны две кружки. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объем второй кружки больше объема первой?

V= πR²h
Так как 1 кружка в полтора раза ниже второй, её высоту возьмем за 1. Тогда высота второй кружки 1,5 *1=1,5. Ширина кружки – это ее диаметр, чтобы найти радиус, разделим его на 2. Вторая кружка в два раза шире второй, значит первая, наоборот в 2 раза уже первой. Ее радиус и берем за 1. Значит радиус второй кружки в 2 раза больше, т.е. 1*2=2. Заполняем таблицу. «Собираем» формулу объема. Вычисляем. Делим большую величину на меньшую.

Ответ: 6

6/1=6

:

Задача 5: Однородный шар диаметром 3 см имеет массу 180 грамм. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см.

V= πR³
Добавляем в таблицу столбец для значений массы. Заполняем таблицу. С помощью пропорции находим значение массы для шара диаметром 2 см.

Ответ: 32

3³
2³

=

108
Х

:

Задача 6: В сосуде имеющем форму конуса уровень жидкости достигает ½ высоты. Объем жидкости равен 30 мл. Сколько миллилитров жидкости нужно долить для заполнения сосуда доверху.

V= πR²h

Ответ: 210

1
8

=

30
Х

Т.к. конус заполнен наполовину, высоту меньшего конуса принимаем равной 1, тогда высота большого конуса в 2 раза больше (т.е.2). Высота и радиус прямо пропорциональные величины, радиус большого конуса также будет в 2 раза больше радиуса малого конуса, который берем за 1. Заполняем таблицу.

240 – 30 = 210

:

Задача 7: Объем конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объем конуса, отсекаемого от данного конуса проведенной плоскостью.

V= πR²h

Ответ: 1

1_
27

=

Х
27

Х=1

Всего частей конуса 1+2=3, т. е. уровень жидкости достигает 1/3 высоты большого конуса. Далее решаем как задачу №6.