Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по математике на тему Тригонометрические уравнения (10 класс)

Содержание

4. *Условные обозначения :tan -тангенсcot - котангенс
5. Решение тригонометрического уравнения состоит из двух этапов: 1.
6. 1. Алгебраический метод. Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ).
7. 2. Разложение на множители. Этот метод рассмотрим на
8. 2. Разложение на множители. П р и
9. П р и м е р 3.
10. 3. Приведение к однородному уравнению. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо: а)
11. П р и м е р
12. 4. Переход к половинному углу. Рассмотрим этот метод
13. 5. Введение вспомогательного угла. Рассмотрим уравнение вида: a sin x + b cos x = c , где a, b, c –
15. 6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
16. 7. Универсальная подстановка. Рассмотрим этот метод на примере.
17. Скачать презентацию
18. Похожие презентации

*Условные обозначения :tan -тангенсcot - котангенс

Главная
Алгебра
Презентация по математике на тему Тригонометрические уравнения (10 класс)

Презентация по математике на тему Тригонометрические уравнения (10 класс)

*Условные обозначения :tan -тангенсcot - котангенс

Решение тригонометрического уравнения состоит из двух этапов: 1. преобразование уравнения для получения его

1. Алгебраический метод. Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ).

2. Разложение на множители. Этот метод рассмотрим на примерах. П р и м

2. Разложение на множители. П р и м е р 2. Решить

П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1. Р е ш

3. Приведение к однородному уравнению. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо: а) перенести все его члены в

П р и м е р . Решить уравнение: 3sin 2 x + 4 sin x · cos x +

4. Переход к половинному углу. Рассмотрим этот метод на примере: П р и

5. Введение вспомогательного угла. Рассмотрим уравнение вида: a sin x + b cos x = c , где a, b, c – коэффициенты; x – неизвестное. Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль

6. Преобразование произведения в сумму. Здесь используются соответствующие формулы. П р и м е р . Решить уравнение: 2 sin 2x · sin 6x = cos 4x. Р е

7. Универсальная подстановка. Рассмотрим этот метод на примере. П р и м е

Слайды презентации

Слайд 4 *Условные обозначения :
tan -тангенс
cot - котангенс

Слайд 5 Решение тригонометрического уравнения состоит из двух этапов: 1. преобразование

Решение тригонометрического уравнения состоит из двух этапов: 1. преобразование уравнения для получения

уравнения для получения его простейшего вида ( см. выше )
2.

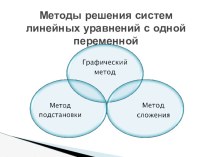
решение полученного простейшего тригонометрического уравнения.

Методы решения тригонометрических уравнений.

Существует семь основных методов решения тригонометрических уравнений.

Слайд 6 1. Алгебраический метод. Этот метод нам хорошо известен из

алгебры
( метод замены переменной и подстановки ).

Слайд 7 2. Разложение на множители. Этот метод рассмотрим на примерах.

2. Разложение на множители. Этот метод рассмотрим на примерах. П р и

П р и м е р 1. Решить уравнение: sin x + cos x =

1 .

    Р е ш е н и е .   Перенесём все члены уравнения влево:

                                                               sin x + cos x – 1 = 0 ,

                               преобразуем и разложим на множители выражение в
                               левой части уравнения:

Слайд 8 2. Разложение на множители.

П р и м

2. Разложение на множители. П р и м е р 2.

е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш

е н и е .     cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

                                            sin x · cos x – sin 2 x = 0 ,

                                            sin x · ( cos x – sin x ) = 0 ,

Слайд 9
П р и м е р 3. Решить

П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1. Р е

уравнение: cos 2x – cos 8x + cos 6x = 1.
Р е ш е н и е . cos 2x + cos 6x =

1 + cos 8x ,

                               2 cos 4x cos 2x = 2 cos ² 4x ,

                               cos 4x · ( cos 2x – cos 4x ) = 0 ,

                               cos 4x · 2 sin 3x · sin x = 0 ,
                              1). cos 4x = 0 ,               2). sin 3x = 0 ,          3). sin x = 0 ,

2. Разложение на множители.

Слайд 10 3. Приведение к однородному уравнению.
Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла.

Чтобы решить однородное уравнение, надо:

а) перенести

все его члены в левую часть;
б) вынести все общие

множители за скобки;
   в) приравнять все множители и скобки нулю;
   г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
        cos ( или sin ) в старшей степени;
   д) решить полученное алгебраическое уравнение относительно tan .

Слайд 11
П р и м е р .

П р и м е р . Решить уравнение: 3sin 2 x +

Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш

е н и е .  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

                             sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

                             tan 2 x + 4 tan x + 3 = 0 ,  отсюда  y 2 + 4y +3 = 0 ,

                             корни этого уравнения:  y1 = -1,  y2 = -3, отсюда
                           1)   tan x = –1,                  2)   tan x = –3,

Слайд 12 4. Переход к половинному углу.
Рассмотрим этот метод на

4. Переход к половинному углу. Рассмотрим этот метод на примере: П р

примере:

П р и м е р . Решить

уравнение: 3 sin x – 5 cos x = 7.
    Р е ш е н и е .
6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
                                                                      = 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
                      2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
                             tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Слайд 13 5. Введение вспомогательного угла.
Рассмотрим уравнение вида:

a sin x + b cos x = c ,

где a, b, c – коэффициенты; x –

неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их

квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь - так называемый вспомогательный угол ), и наше уравнение принимает вид:

Слайд 14

Слайд 15 6. Преобразование произведения в сумму.
Здесь используются соответствующие формулы.

П р и м е р . Решить

6. Преобразование произведения в сумму. Здесь используются соответствующие формулы. П р и м е р . Решить уравнение: 2 sin 2x · sin 6x = cos 4x. Р

уравнение: 2 sin 2x · sin 6x = cos 4x.

Р е ш е н и е

. Преобразуем левую часть в сумму:

                                        cos 4x – cos 8x = cos 4x ,

                                                 cos 8x = 0 ,

                                                 8x = p / 2 + pk ,

                                                 x = p / 16 + pk / 8 .