лежащие на прямой, переходят в точки, лежащие на прямой,
причем порядок взаимного расположения точек на прямой сохраняется.Докозательство:
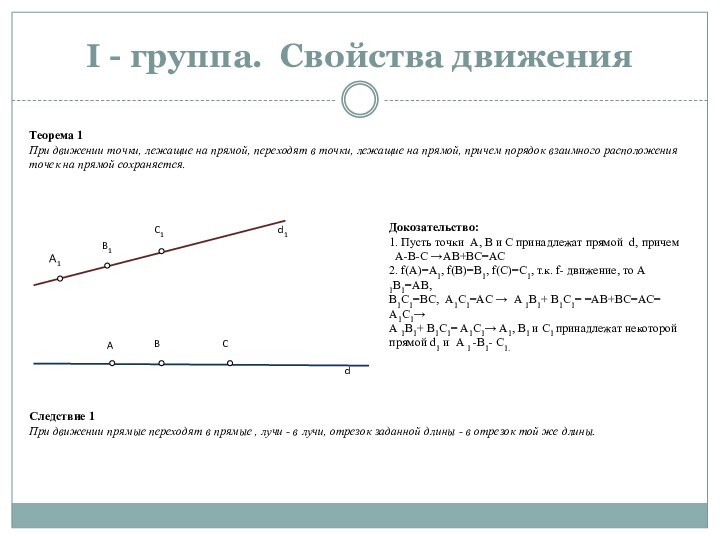
1. Пусть точки А, В и С принадлежат прямой d, причем
А-В-С →АВ+ВС=АС
2. f(A)=A1, f(В)=В1, f(С)=С1, т.к. f- движение, то А 1В1=АВ,
В1С1=ВС, А1С1=АС → А 1В1+ В1С1= =АВ+ВС=АС= А1С1→
А 1В1+ В1С1= А1С1→ A1, В1 и С1 принадлежат некоторой прямой d1 и А 1 -В1- С1.
Следствие 1
При движении прямые переходят в прямые , лучи - в лучи, отрезок заданной длины - в отрезок той же длины.