- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дифференциальное исчисление функции одной переменной
Содержание
- 2. Дифференциальное исчисление функции одной переменной.
- 3. Определение производной Производной функции y=f(x) в точке
- 4. Таблица производных
- 7. Правила ДифференцированияПусть u=u(x) и v=v(x) – функции,
- 8. Производная сложной функции Пусть y=f(u), а u=φ(x).
- 10. Дифференцирование функций, заданных параметрически Пусть функция y
- 11. Примерx=cos3t, y=sin3t. Вычислить yx´´. поэтому
- 12. Дифференцирование функций, заданных неявно.Вычислить y´x, если y5+xy-x2=0.Продифференцируем обе части по х. Получим 5y4y´+y+xy´-2x=0, откуда y´(5y4+x)=2x-y и
- 13. Логарифмическое дифференцирование Найти производную функции y=(sinx)x.Логарифмируем функцию
- 14. Дифференциал функции dy=f´(x)∙dx
- 15. Некоторые теоремы о дифференцируемых функциях!
- 16. Теорема Ферма Пусть функция y=f(x) определена в
- 17. Теорема Ролля Пусть функция y=f(x) непрерывна на
- 18. Теорема Лагранжа Пусть функция y=f(x) непрерывна на
- 19. Теорема Лопиталя (правило Лопиталя). Пусть f(x) и
- 20. Пример
- 21. Применение производной к исследованию функций
- 22. Экстремумы функции.
- 23. Необходимо условие монотонности функции Если дифференцируемая в
- 24. Достаточный признак существования экстремума Если непрерывная на
- 25. Выпуклость и вогнутость графика функции График дифференцируемой
- 26. Достаточный признак выпуклости и вогнутости Пусть функция
- 27. Достаточный признак существования точки перегиба Если вторая
- 28. Асимптоты графика функции Асимптотой графика функции y=f(x)
- 29. План исследования функции и построение графика Область
- 30. Пример Исследовать функцию
- 31. 2. Пусть х=0, тогда у=0. Пусть у=0,
- 33. 4. Функция имеет разрывы в точках х=-2
- 34. 5.Невертикальные асимптоты следовательно, прямая у=1 – асимптота.
- 35. 6.у´=0, если -8х=0, откуда х=0 – критическая
- 36. 7.у´´≠0 при х(-∞;∞), х=-2 и х=2 –
- 37. Скачать презентацию
- 38. Похожие презентации
Дифференциальное исчисление функции одной переменной.
















![Дифференциальное исчисление функции одной переменной Теорема Ролля Пусть функция y=f(x) непрерывна на отрезке [a;b], дифференцируема на интервале](/img/tmb/13/1285294/a3c33fee0e51b4ab714990903799487d-720x.jpg)
![Дифференциальное исчисление функции одной переменной Теорема Лагранжа Пусть функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в](/img/tmb/13/1285294/08c4d55d1259a35fc4fc1497e98015c9-720x.jpg)













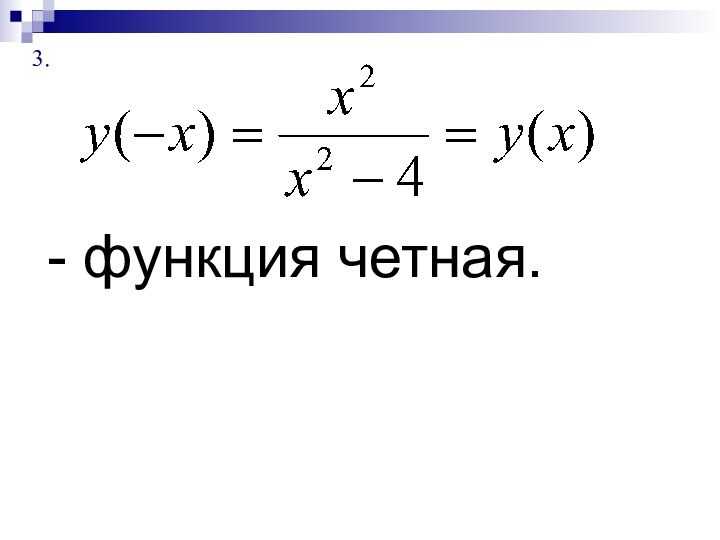




Слайд 7
Правила Дифференцирования
Пусть u=u(x) и v=v(x) – функции, дифференцируемые
в точке х. Тогда в этой точке дифференцируемы функции
u+v, u∙v, . Последнее при условии, что v´(x)≠0. Причем, (u+v)´=u´+v´, (uv)´=u´v+uv´, .
Слайд 8
Производная сложной функции
Пусть y=f(u), а u=φ(x). Тогда
функция y=f(φ(x)) называется сложной функцией от х.
Теорема. Если
функция u=φ(x) имеет производную в точке х, а функция y=f(u) имеет производную в соответствующей точке u=φ(x), то сложная функция y=f(φ(x)) имеет производную в точке х, причем .
Слайд 10
Дифференцирование функций, заданных параметрически
Пусть функция y от
х задана параметрически уравнениями: x=x(t), y=y(t), t
(α;β).
Слайд 12
Дифференцирование функций, заданных неявно.
Вычислить y´x, если y5+xy-x2=0.
Продифференцируем обе
части по х. Получим 5y4y´+y+xy´-2x=0, откуда y´(5y4+x)=2x-y и
Слайд 13
Логарифмическое дифференцирование
Найти производную функции y=(sinx)x.
Логарифмируем функцию по
основанию е: lny=x.lnsinx. Дифференцируем обе части равенства по х:
∙y´=lnsinx+x∙ctgxотсюда y´=y∙(lnsinx+x∙ctgx) или y´=(sinx)x∙(lnsinx+x∙ctgx).
Слайд 16
Теорема Ферма
Пусть функция y=f(x) определена в интервале
(a;b) и принимает в точке с этого интервала наибольшее
или наименьшее на (a;b) значение. Если существует f´(c), то f´(c)=0
Слайд 17
Теорема Ролля
Пусть функция y=f(x) непрерывна на отрезке
[a;b], дифференцируема на интервале (a;b) и f(a)=f(b)=0. Тогда ее
производная f´(х) обращается в ноль хотя бы в одной точке c (a;b).
Слайд 18
Теорема Лагранжа
Пусть функция y=f(x) непрерывна на отрезке
[a;b] и дифференцируема в интервале (a;b). Тогда существует хотя
бы одна точка c (a;b), для которой выполняется условие:
Слайд 19
Теорема Лопиталя (правило Лопиталя).
Пусть f(x) и φ(x)
– функции, непрерывные на [a;b], дифференцируемые на (a;b); φ´(x)≠0
при всех х (a;b) и f(a)=φ(a)=0. Тогда если существует , то существует причем :
Слайд 23
Необходимо условие монотонности функции
Если дифференцируемая в интервале
(a;b) функция y=f(x) возрастает (убывает) на (a;b), то для
всех х(a;b) f´(x)≥0 (f´(x)≤0)
Слайд 24
Достаточный признак существования экстремума
Если непрерывная на интервале
функция y=f(x) имеет производную f´(x) во всех точках этого
интервала, за исключением, может быть, критической точки с, принадлежащей этому интервалу, и если f´(x) при переходе аргумента слева направо через критическую точку с меняет знак с плюса на минус (с минуса на плюс), то функция в точке с имеет максимум (минимум)
Слайд 25
Выпуклость и вогнутость графика функции
График дифференцируемой функции
называется выпуклым (вогнутым) в интервале (a;b), если он расположен
ниже (выше) любой своей касательной на этом интервале
Слайд 26
Достаточный признак выпуклости и вогнутости
Пусть функция y=f(x)
имеет вторую производную f´(x) во всех точках интервала (a;b).
Если во всех точках этого интервала f´(x)<0 (f´(x)>0), то график на (a;b) выпуклый (вогнутый).
Слайд 27
Достаточный признак существования точки перегиба
Если вторая производная
f´(x) непрерывной функции меняет знак при переходе аргумента через
точку х0, то точка (x0;f(x0)) является точкой перегиба графика функции.
Слайд 28
Асимптоты графика функции
Асимптотой графика функции y=f(x) называется
прямая, расстояние от которой до текущей точки графика функции
стремится к нулю при неограниченном удалении этой точки от начала координат.
Слайд 29
План исследования функции и построение графика
Область определения
функции.
Точки пересечения графика функции с осями координат.
Четность, нечетность функции.
Исследование
функции на непрерывность. Вертикальные асимптоты.Невертикальные асимптоты.
Интервалы монотонности и экстремумы.
Интервалы выпуклости, вогнутости и точки перегиба.
Дополнительные точки, , периодичность (по мере необходимости).
Построение графика.
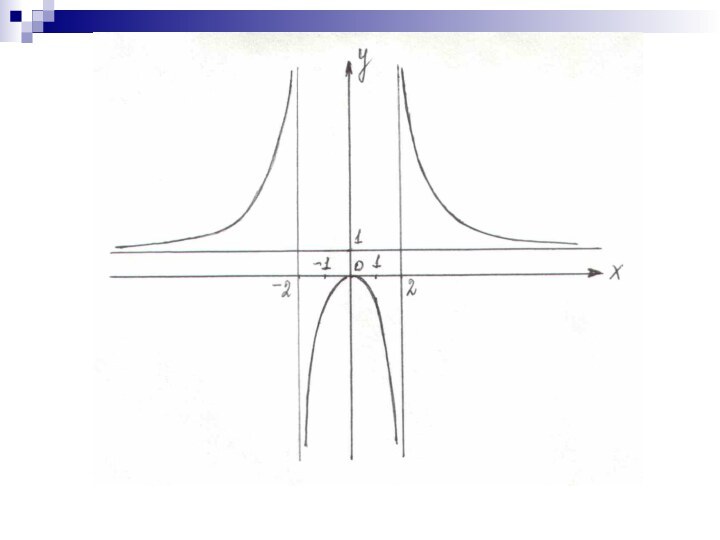
Слайд 30 Пример Исследовать функцию
и построить ее график.
Область определения:
так как
при х=-2 и х=2 знаменатель дроби обращается в ноль.(-∞;-2) (-2;2) (2;+∞),
Слайд 31
2. Пусть х=0, тогда у=0. Пусть у=0,
тогда , откуда х=0.
(0;0) –
точка пересечения графика с осями координат Слайд 33 4. Функция имеет разрывы в точках х=-2 и
х=2, так как f(-2) и f(2) не определены.
, ,
, ,
следовательно, х=-2 и х=2 – точки разрыва II рода и прямые х=-2 и х=2 – вертикальные асимптоты.
Слайд 35
6.
у´=0, если -8х=0, откуда х=0 – критическая точка.
Откуда х=-2 и х=2 – критические точки.
На интервалах (-∞;-2) и (-2;0) функция возрастает, а на интервалах (0;2) и (2;+∞) – убывает.Уmax(0)=0.