Презентация на тему Задачи на построение 7 класс

Слайд 1 Задачи на построение
Геометрия 7 класс по Л.С. Атанасяну
Махмудова Наталья Юрьевна
учитель

математики МБОУ СОШ № 18
имени Э.Д.Потапова г.Мичуринска

---

Слайд 2 Дано:
№ 313
Построить:
∆ ABC, где BD - медиана
Анализ:
A
B
C
D
A
B
B
C
B
D
B1

---

Слайд 3 Описание построения:
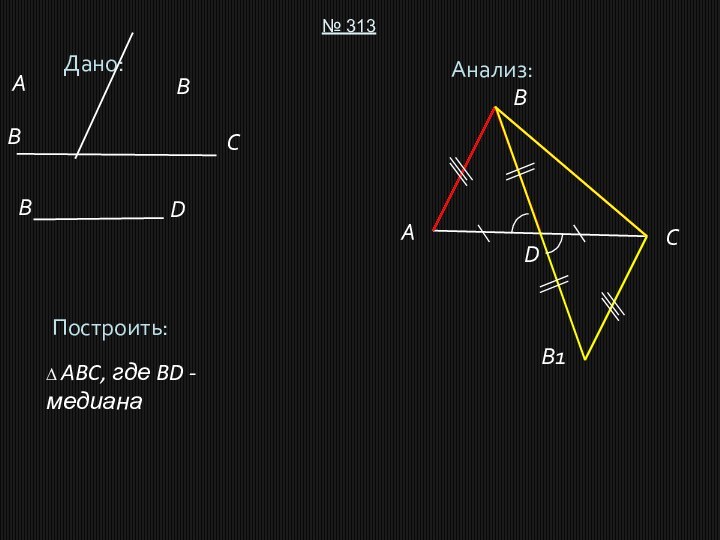
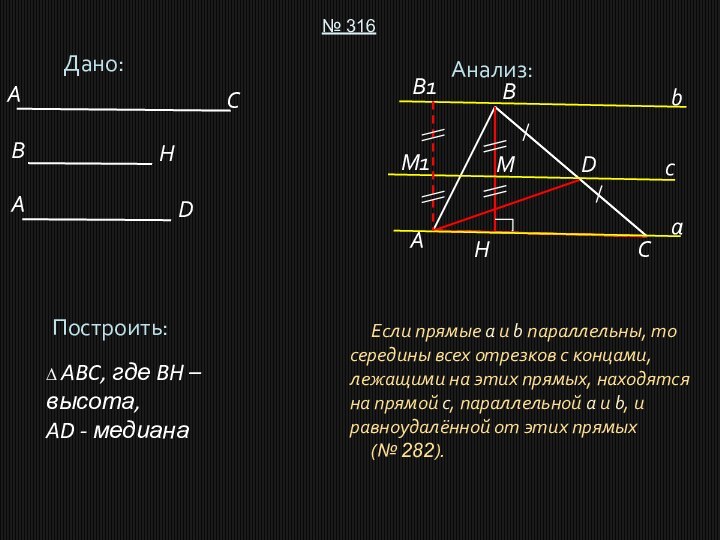
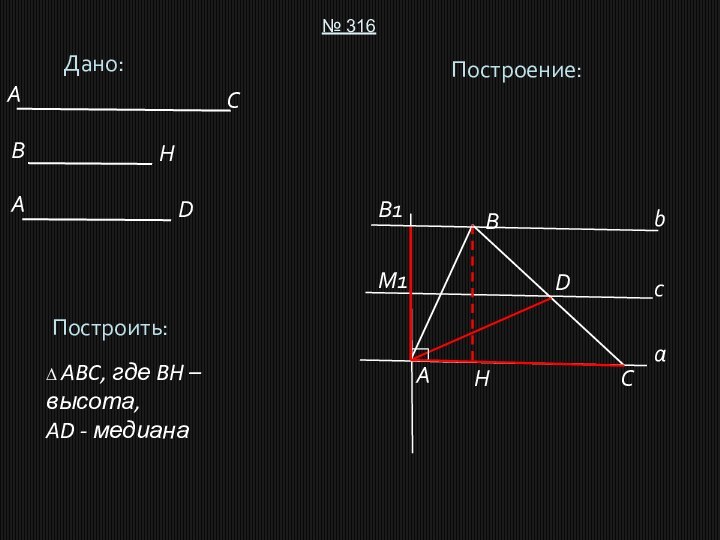
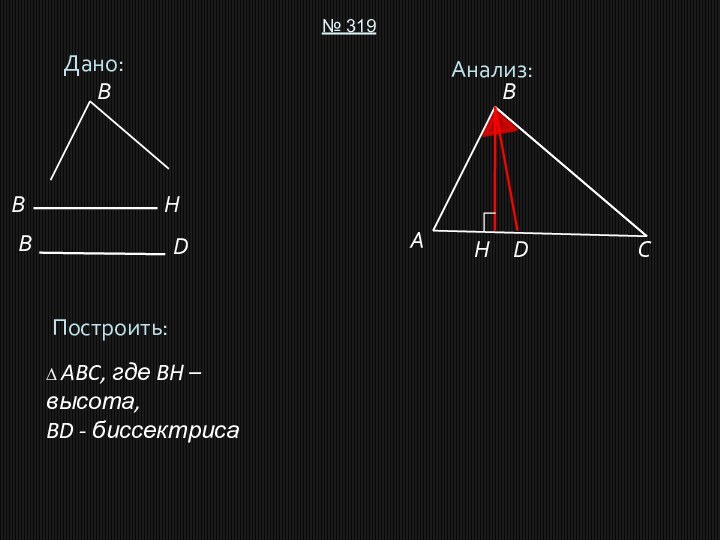
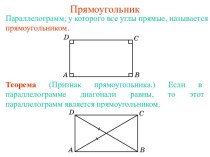
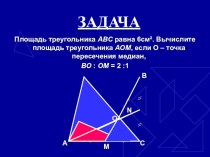
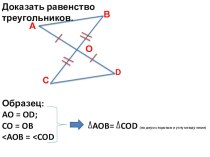
1. Строим ∆BCB1 по трём сторонам (BB1 =

2BD, CB1 = AB).
2. Строим точку D – середину BB1.
3.* На продолжении луча CD от точки D откладываем отрезок, равный CD (получили точку A).
4. Проводим сторону AB.
5. ∆ABC – искомый.

Задача имеет решение и при том только одно, если для отрезков AB, BC и 2BD выполняется неравенство треугольника.

---

Слайд 4 Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Анализ:
A
B
C
D
A
C
B
D
H
H
A
Если прямые

a и b параллельны, то середины всех отрезков с концами, лежащими на этих прямых, находятся на прямой с, параллельной a и b, и равноудалённой от этих прямых
(№ 282).

b

a

M

с

M1

B1

---

Слайд 5 Описание построения:
1. Строим две перпендикулярные прямые (получили точку A).
На

одной из сторон прямого угла от точки A откладываем отрезок равный HB (получили точку B1).
3. От точки A на прямой a откладываем отрезок равный AC (получили точку C).
4. Строим точку M1 – середину отрезка AB1.
5. Через точку M1 проводим прямую c, параллельную прямой a.
6. Через точку B1 проводим прямую b, параллельную прямой a
7. Из точки A раствором циркуля равным AD проводим дугу до пересечения с прямой c (получили точку D).
8. Через точки C и D проводим прямую (получили точку B).
9. Проводим сторону AB.
10. ∆ABC – искомый.

Задача не всегда имеет решение. Если решение есть, то оно единственное.

---

Слайд 6 Дано:
№ 316
Построить:
∆ ABC, где BH – высота,
AD - медиана
Построение:
A
B
C
D
A
C
B
D
H
H
A
a
M1
с
B1
b

---

Слайд 7 Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Анализ:
A
B
C
D
B
B
D
H
H
B

---

Слайд 8 Описание построения:
1. Построим прямоугольный треугольник HBD по гипотенузе и

катету.
Проведём биссектрису данного угла B (получим угол ABD).
Достроим угол DBH треугольника HBD до угла DBA, равного половине угла A (получим точку A).
4. Достроим угол ABD до угла ABC (получим точку C)
5. ∆ABC – искомый.

Задача всегда имеет решение и при том единственное.

---

Слайд 9 Дано:
№ 319
Построить:
∆ ABC, где BH – высота,
BD - биссектриса
Построение:
A
B
C
D
B
B
D
H
H
B

---

Слайд 10

---