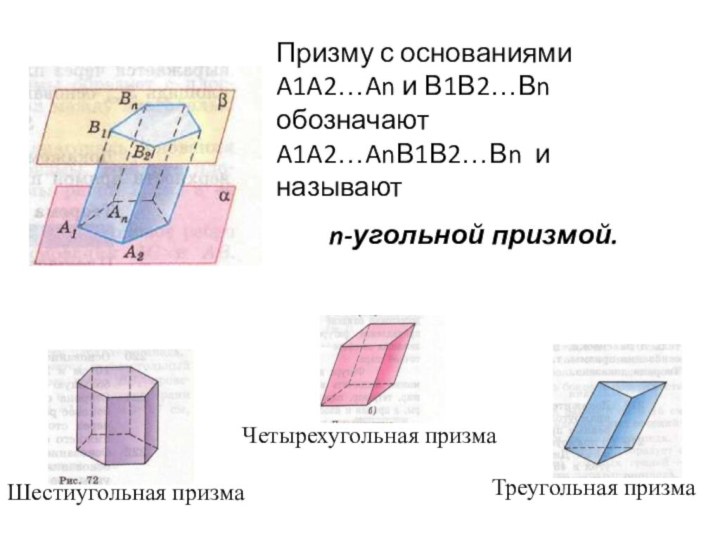
в параллельных плоскостях α и , так
что отрезки А1В1, А2В2, …, AnBn, соединяющие соответственные вершины многоугольников параллельны. Каждый из n четырех-угольников А1А2В2В1, …, AnA1B1Bn - параллелограмм.(Почему?)
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.