- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинаторика
Содержание
- 2. Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал»:Определение 1:n!=1·2·3·…·(n-2)·(n-1)·n
- 3. Например:6!=1·2·3·4·5·6=720·····!=
- 4. Теорема 1:n различных элементов можно расставить по
- 5. 6 слонятСколькими способами можно их расставить?Например:6!=1·2·3·4·5·6=720
- 6. Задача 1:К хозяину дома пришли гости A,B,C,D.
- 7. Решение:а) На 5 стульев должны сесть 5
- 8. Решение:б) Так как место хозяина фиксировано, то
- 9. Задача 2:В чемпионате по футболу участвовало 7
- 10. Решение:Первый способ:Рассмотрим таблицу 7х7, в которой вписаны
- 11. Решение:В нижней части таблицы результатов нет, т.к.
- 12. Второй способ:Произвольно пронумеруем команды №1, №2,…, №7
- 13. Третий способ:Используем геометрическую модель: 7 команд –
- 14. Выводы:Состав игры определен, как только мы выбираем
- 15. Теорема 2:Если множество состоит из n элементов
- 16. Определение 2:Число всех выборов двух элементов без
- 17. Задача 3:Встретились 11 футболистов и 6 хоккеистов
- 18. Решение:а) б) в)
- 19. А что получится, если мы будем учитывать
- 20. Определение 3:Число всех выборов двух элементов с
- 21. Задача 4:В классе 27 учеников. К доске
- 22. А как будут выглядеть формулы, если в
- 23. Теорема 4:Для любых натуральных чисел n и k таких, что k
- 24. ЗАДАЧИ
- 25. Задача 5:В классе 27 учеников, из них
- 26. Скачать презентацию
- 27. Похожие презентации
























Слайд 2 Произведение подряд идущих первых n натуральных чисел обозначают
n! и называют «эн факториал»:
Слайд 4
Теорема 1:
n различных элементов можно расставить по одному
на n различных мест ровно n! способами.
Рn=n! - перестановки
Слайд 6
Задача 1:
К хозяину дома пришли гости A,B,C,D. За
круглым столом – пять разных стульев.
а) Сколькими способами можно
рассадить гостей за столом?б) Сколькими способами можно рассадить гостей за столом, если место хозяина дома уже известно?
A
B
C
D
хозяин
Слайд 7
Решение:
а) На 5 стульев должны сесть 5 человек
(включая хозяина дома). Значит, всего имеется Р5 способов их
рассаживания:Р5 =5!=
1·2·3·4·5=
120
Слайд 8
Решение:
б) Так как место хозяина фиксировано, то следует
рассадить четырех гостей на четыре места. Это можно сделать
Р4 способами:Р4 =4!=
1·2·3·4=
24
Слайд 9
Задача 2:
В чемпионате по футболу участвовало 7 команд.
Каждая команда сыграла по одной игре с каждой командой.
Сколько всего было игр?
Слайд 10
Решение:
Первый способ:
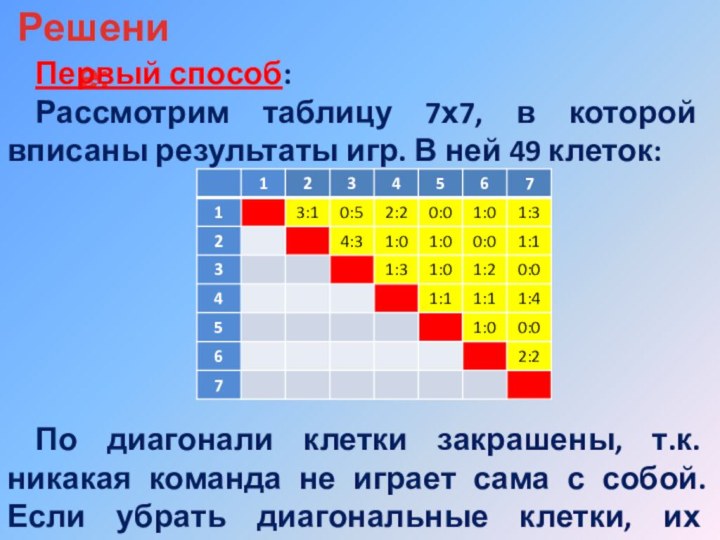
Рассмотрим таблицу 7х7, в которой вписаны результаты
игр. В ней 49 клеток:
По диагонали клетки закрашены, т.к.
никакая команда не играет сама с собой. Если убрать диагональные клетки, их останется 49-7=42.
Слайд 11
Решение:
В нижней части таблицы результатов нет, т.к. все
они получаются отражением уже имеющихся результатов из верхней части
таблицы.3:1
1:3
Поэтому количество всех проведенных игр равно половине от 42, т.е. 21.
Слайд 12
Второй способ:
Произвольно пронумеруем команды №1, №2,…, №7 и
посчитаем число игр поочередно. Команда №1 встречается с командами
№2-7 – это 6 игр. Команда №2 тоже проведет 6 встреч, но одну игру , с командой №1, мы уже посчитали. Получается 5 новых игр. Команда №3 проведет 6 встреч, из которых две, с №1 и №2 мы посчитали, значит, добавится еще 4 игры. Продолжая, получим:6 игр
5 игр
4 игры
3 игры
2 игры
1 игра
21 игра
6+5+4+3+2+1=21
Слайд 13
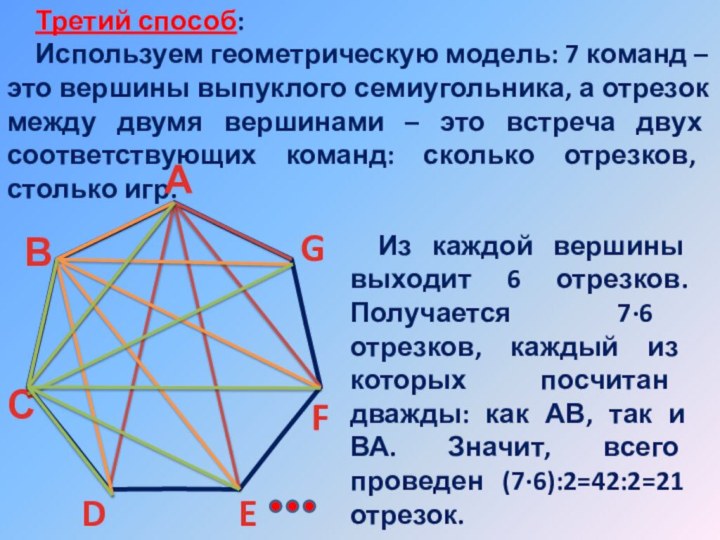
Третий способ:
Используем геометрическую модель: 7 команд – это
вершины выпуклого семиугольника, а отрезок между двумя вершинами –
это встреча двух соответствующих команд: сколько отрезков, столько игр.Из каждой вершины выходит 6 отрезков. Получается 7·6 отрезков, каждый из которых посчитан дважды: как АВ, так и ВА. Значит, всего проведен (7·6):2=42:2=21 отрезок.
А
В
С
D
E
F
G
Слайд 14
Выводы:
Состав игры определен, как только мы выбираем две
команды. Значит, количество всех игр в турнире для n
команд – это количество всех выборов двух элементов из n данных элементов. При этом порядок выбора не важен.
Слайд 15
Теорема 2:
Если множество состоит из n элементов и
требуется выбрать два элемента без учета их порядка, то
такой выбор можно произвестиспособами.
Слайд 16
Определение 2:
Число всех выборов двух элементов без учета
их порядка из n данных элементов называют числом сочетаний
из n элементов по 2 и обозначают[«цэ из эн по два»]
Слайд 17
Задача 3:
Встретились 11 футболистов и 6 хоккеистов и
каждый стал по одному разу играть с каждым в
шашки, которые они «давненько не брали в руки». Сколько встреч было:а) между футболистами
б) между хоккеистами
в) всего?
Слайд 19 А что получится, если мы будем учитывать порядок
двух выбираемых элементов?
Теорема 3:
Если множество состоит из n элементов
и требуется выбрать два элемента учитывая их порядок, то такой выбор можно произвести способами.
Слайд 20
Определение 3:
Число всех выборов двух элементов с учетом
их порядка из n данных элементов называют числом размещений
из n элементов по 2 и обозначают[«а из эн по два»]
Слайд 21
Задача 4:
В классе 27 учеников. К доске нужно
вызвать двоих. Сколькими способами это можно сделать, если:
а) первый
ученик должен решить задачу по алгебре, а второй – по геометрии;б) они должны быстро стереть с доски?
Решение:
В случае а) порядок важен, а в случае б) – нет. Значит,
а)
б)
Слайд 22 А как будут выглядеть формулы, если в них
верхний индекс заменить на 5, 7, 10 и т.д.?
Сколькими способами можно выбрать 5 учеников из 30 для дежурства в столовой; 7 монет из 10 данных; 10 карт из колоды в 32 карты?Определение 4:
Число всех выборов k элементов из n данных без учета порядка называют числом сочетаний из n элементов по k и обозначают
Число всех выборов k элементов из n данных с учетом их порядка называют числом размещений из n элементов по k и обозначают
Слайд 25
Задача 5:
В классе 27 учеников, из них нужно
выбрать троих. Сколькими способами это можно сделать, если:
а) первый
ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую?б) им следует спеть в хоре?