Слайд 2
Опр.: Упорядоченные координатные оси, не лежащие в одной
плоскости и имеющую одну общую точку, называются косоугольной системой
координат в пространстве.
Если координатные оси взаимно перпендикулярны, то косоугольную систему координат называют прямоугольной системой координат Декарта в пространстве и обозначают хуz.
Опр.: Множество упорядоченных троек чисел в избранной системе координат называется трехмерным пространством.
z
z1
P(х1; у1; z1)
у1 у
х1
х
Элементы системы координат:
координатные плоскости Оху, Оуz, Охz;
оси координат: Ох – ось абсцисс, Оу – ось ординат; Оz – ось аппликат.
Точка О – начало координат;
упорядоченная тройка чисел (х; у; z) – координаты произвольной точки Р.
у
у1 Р(х1; у1)
0 х1 х
Частным случаем является система координат на плоскости, например координатная плоскость Оху.
у
Р (х1; у1)
r
φ
0 А х
Точка на плоскости может быть задана полярной системой координат, при этом положение точки Р описывается углом поворота положительной полуоси Ох против часовой стрелки до положения луча ОР и расстоянием точки Р от начала координат.
Из Δ АРО, где
, имеем:
Слайд 5
Примеры
1) Задать точку плоскости А (-1; 1) в
полярных координатах.
Решение. r=
Таким образом А
2) Задать точку плоскости В (0,5; π/4) в декартовых координатах.
Решение.
х1=0,5cosπ/6 =0,5
у1=0,5sin π/6= 0,5·1/2 .
Таким образом В (0,25 ; 0,25)
Слайд 6
Прямые на плоскости
Прямая на координатной плоскости может быть
получена в результате пересечения произвольной плоскости
Ах + Ву + Сz + D = 0 и координатной плоскости.
Составим уравнение прямой, принадлежащей, например, плоскости хОу. Эта прямая определяется системой двух уравнений:
Слайд 7
Таким образом Ах + Ву + С =
0 (*) – общее уравнение прямой на координатной плоскости,
причем (А; В) является нормальным вектором этой прямой.
n L
Опр.: геометрическое место точек, удовлетворяющее уравнению (*), называется прямой.
у
b - уравнение прямой в отрезках на осях
а
0 L у
L - уравнение прямой,
М1(х1;у1) М2(х2;у2) проходящей через две точки
у
L
b
φ
0 х
L: у= kх+b, где k= tgφ – уравнение прямой с угловым коэффициентом;
L: у – у1= k (х – х1) – уравнение прямой с угловым коэффициентом, проходящей через т. М (х1; у1).
Слайд 9
Угол между прямыми
Пусть прямые заданы уравнением
А1х + В1у
+ С1 =0 и А2х + В2у + С2
=0
Угол между этими прямыми найдем из формулы:
Если прямые заданы уравнением с угловыми коэффициентами, то угол между ними находим по формуле:
Слайд 10
y L2
L1
0
х
Условия параллельности и перпендикулярности
двух прямых:
L1||L2, если
или k1=k2
L1 L2, если А1А2= -В1В2 или k1k2= -1
φ
Слайд 11
Примеры
1. Определить острый угол между прямыми у
= 3х + 1 и у = -2х
– 5.
Решение. Полагая k1= 3 и k2= -2 и применяя формулу (1), получим
tg ϕ = -2–3/1+(-2)⋅3= -5/-5= 1, т.е. ϕ = π/4= 0,785 рад.
2. Показать, что прямые 7х + 3у – 5 = 0 и 14х + 6у + 1 = 0 параллельны.
Решение. Приведя уравнение каждой прямой к виду с угловым коэффициентом, получаем:
у= -7/3х+5/3 и у= -7/3х+1/14.
Угловые коэффициенты этих прямых равны: k1= k2= -7/3, т. е. прямые параллеьны.
3. Даны вершины треугольника А (-5; 0), В (-3; -2) и С (-7; 6). Найти уравнения высот треугольника AD, BN и CM.
Решение. По формуле (4) найдем угловой коэффициент стороны ВС:
kВС= 6+2/-7–(-3)= 8/-4= -2.
В силу перпендикулярности прямых AD и BC kAD= -1/kВС, т. е. kAD= ½.
Уравнение высоты, проведенной из вершины А будет иметь вид:
у–0= ½(х+5) или х–2у+5= 0.
Слайд 12
Линии второго порядка на плоскости
Слайд 13
Линии второго порядка на плоскости.
Общее уравнение линии второго
порядка на плоскости:
а11х2 + а22у2 + 2а12ху + а10х
+ а20у + а00 = 0, где а211 + а212 + а222 ≠ 0, т. е. хотя бы одно из чисел а11,а12,а22 не равно нулю.
Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки (центра).
Слайд 14
Каноническое уравнение
окружности с центром в точке М(х0;у0) и радиусом R.
Уравнение окружности с центром в начале координат
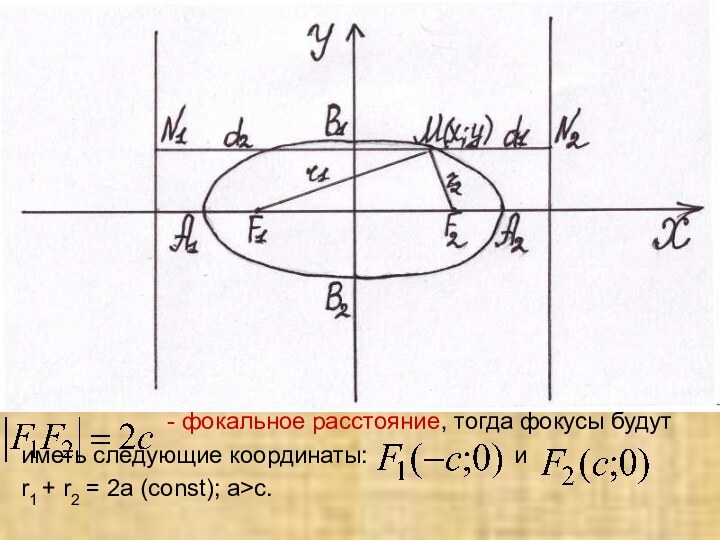
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
- фокальное расстояние, тогда фокусы будут
иметь следующие координаты: и
r1 + r2 = 2а (const); a>c.
r1 =
, r2 = , тогда
аналитическое уравнение эллипса примет вид:
Обозначив , получим каноническое уравнение эллипса:
Слайд 17
Свойства эллипса
Эллипс – ограниченная кривая второго порядка.
Эллипс имеет
вертикальную и горизонтальную оси симметрии, а так же центр
симметрии.
А1 А2 - большая ось (ОА1 - полуось), В1 В2 – малая ось (ОВ1 - полуось).
А1, А2, В1, В2 - вершины эллипса, причем
- называется эксцентриситетом эллипса,
,т.е. 0< <1;
- характеризует: “вытянутость эллипса, т.е. отклонение от окружности”.
=1, значит x2+y2 = a2, где а – радиус окружности
называются директрисами
(направляющими)
т.о. имеем: , где d1=
Пример:
Дан эллипс найти полуоси, эксцентриситет,
уравнения директрис.
Слайд 19
Гипербола
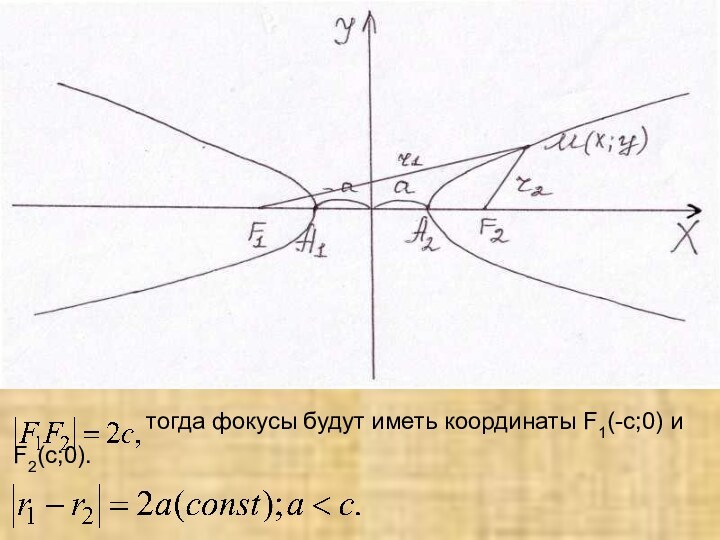
Определение: Гиперболой называется множество точек плоскости, модуль разности
расстояний каждой из которых до двух данных точек, называемых
фокусами, есть величина постоянная.
тогда фокусы будут иметь координаты F1(-c;0) и
F2(c;0).
,
r2 = , тогда
аналитическое уравнение гиперболы примет вид:
Обозначив , получим каноническое уравнение гиперболы:
Слайд 23
Свойства гиперболы
Гипербола – неограниченная кривая второго порядка.
Гипербола обладает
центральной симметрией.
А1, А2 – действительные вершины гиперболы; ось 2а
– действительная, 2b – мнимая.
Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты:
Эксцентриситет гиперболы:
причем
Прямые - называется директрисами гиперболы
причем
Слайд 24
Примеры: Дана гипербола 16х2 – 9у2 = 144,
найти: полуоси а и b; фокусы; эксцентриситет; уравнения асимптот;
уравнения директрис.
16х2 – 9у2 = 144
1.
2.
3.
4.
5.
Слайд 25
Парабола
Определение: параболой называется множество точек плоскости, равноудаленных от
фиксированной точки плоскости(фокус F) и фиксированной прямой (директриса d).
тогда
аналитическое уравнение параболы примет вид:
таким образом получим каноническое уравнение параболы:
Слайд 28
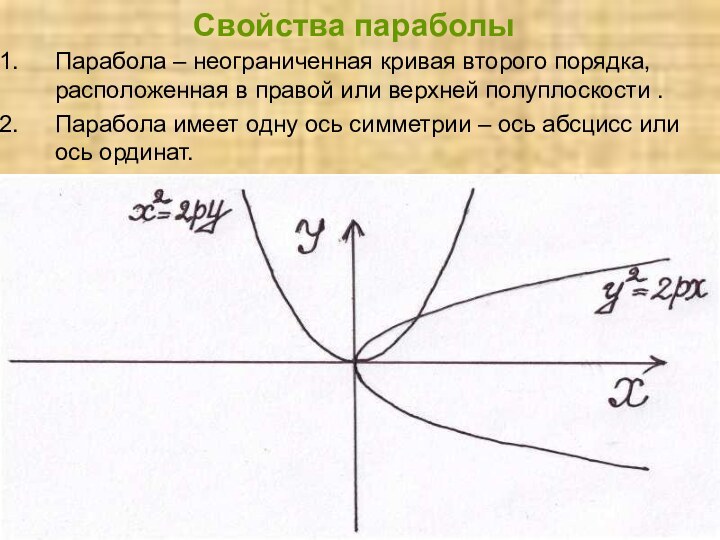
Свойства параболы
Парабола – неограниченная кривая второго порядка, расположенная
в правой или верхней полуплоскости .
Парабола имеет одну ось
симметрии – ось абсцисс или ось ординат.