- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аналитическая геометрия
Содержание
- 2. § Прямая на плоскости 1. Общее
- 3. ВЫВОДЫ:1) Прямая на плоскости является линией первого
- 4. ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПРЯМОЙ. Если в уравнении
- 5. 2) Пусть в общем уравнении прямой коэффициенты
- 6. 3) Пусть в общем уравнении прямой один
- 7. Замечание. Пусть прямая ℓ не проходит
- 8. 2. Другие формы записи уравнения прямой на
- 9. 2) Каноническое уравнение прямой на плоскости3) Уравнение
- 10. 4) Уравнение прямой с угловым коэффициентом
- 11. Пусть прямая ℓ не параллельна оси Ox
- 12. Уравнение y – y1 = k·(x –
- 13. 3. Взаимное расположение прямых на плоскости На
- 14. Получаем, что прямые ℓ1 и ℓ2 параллельны
- 15. 2) Пусть прямые пересекаютсягде знак плюс берется
- 16. где знак плюс берется в том случае,
- 17. 4. Расстояние от точки до прямойЗАДАЧА 3.
- 18. § Плоскость 1. Общее уравнение плоскости и
- 19. ВЫВОДЫ: 1) Плоскость является поверхностью первого порядка.
- 20. ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИЕсли в уравнении Ax+By+Cz+D
- 21. 2) Пусть в общем уравнении плоскости коэффициенты
- 22. а) плоскость отсекает на осях Ox и
- 23. б) плоскость отсекает на осях Ox и
- 24. 4) Пусть в уравнении плоскости (2) два
- 25. б) плоскость отсекает на Oy отрезок b
- 26. 5) Пусть в общем уравнении плоскости (2)
- 27. 6) Пусть в общем уравнении плоскости (2)
- 28. Замечание. Пусть плоскость λ не проходит через
- 29. 2. Другие формы записи уравнения плоскости1) Уравнение
- 31. 2) Уравнение плоскости, проходящей через три точки, не
- 32. 3. Взаимное расположение плоскостей В пространстве две
- 33. 1) Пусть плоскости параллельны:Получаем, что плоскости λ1
- 34. 2) Пусть плоскости пересекаютсягде знак плюс берется
- 35. Частный случай – плоскости перпендикулярны, т.е. критерий перпендикулярности плоскостей, заданных общими уравнениями.
- 36. 4. Расстояние от точки до плоскостиЗАДАЧА 3.
- 37. § Прямая в пространстве 1. Уравнения прямой
- 38. Другие формы записи уравнений прямой в пространстве
- 39. называют параметрическими уравнениями прямой в пространстве (в векторной и координатной форме соответственно).
- 40. Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ,
- 41. 2. Переход от общих уравнений прямой к
- 42. 3. Взаимное расположение прямых в пространстве В
- 43. 2) Пусть прямые ℓ1 и ℓ2 пересекаются:Получили:
- 44. 4. Задачи, связанные с возможным взаимным расположением
- 45. ЗАДАЧА 2. Найти угол между пересекающимися (скрещивающимися)
- 46. ЗАДАЧА 3. Найти расстояние от точки до прямой в пространстве.
- 47. ЗАДАЧА 4. Найти расстояние между скрещивающимися
- 48. Тогда d – высота пирамиды, опущенная из точки M2. Следовательно:
- 49. ЗАДАЧА 5. Найти точку пересечения прямых. Пусть
- 50. 5. Взаимное расположение прямой и плоскости в
- 51. а) Если прямая параллельна плоскости или прямая принадлежит
- 52. Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и плоскости
- 53. Скачать презентацию
- 54. Похожие презентации

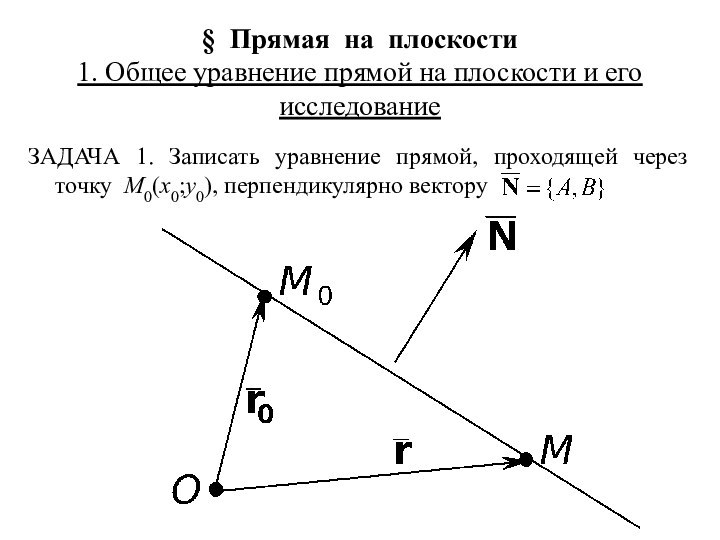


















































Слайд 2 § Прямая на плоскости 1. Общее уравнение прямой
на плоскости и его исследование
прямой, проходящей через точку M0(x0;y0), перпендикулярно вектору
Слайд 3
ВЫВОДЫ:
1) Прямая на плоскости является линией первого порядка.
В общем случае она задается уравнением Ax+By+C = 0,
где A,B,C – числа.2) Коэффициенты A и B не обращаются в ноль одновременно, так как с геометрической точки зрения это координаты вектора, перпендикулярного прямой.
Вектор, перпендикулярный прямой, называют нормальным вектором этой прямой.
Слайд 4
ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПРЯМОЙ.
Если в уравнении Ax+By+C
= 0 все коэффициенты A,B и C отличны от
нуля, то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – уравнение называют неполным.1) Пусть общее уравнение прямой – полное. Тогда его можно записать в виде
С геометрической точки зрения a и b – отрезки, отсекаемые прямой на координатных осях Ox и Oy соответственно. Уравнение (5) называют уравнением прямой в отрезках.
Слайд 5 2) Пусть в общем уравнении прямой коэффициенты A
и B – ненулевые, а C = 0, т.е.
уравнение прямой имеет видAx+By = 0.
Такая прямая проходит через начало координат O(0;0).
Слайд 6 3) Пусть в общем уравнении прямой один из
коэффициентов A или B – нулевой, а C ≠
0, т.е. уравнение прямой имеет видAx+C = 0 или By+C = 0.
Эти уравнения можно записать в виде
x = a и y = b .
4) Пусть в общем уравнении прямой C = 0 и один из коэффициентов A или B тоже нулевой, т.е. уравнение прямой имеет вид Ax = 0 или By = 0.
Эти уравнения можно записать в виде
x = 0 (уравнения координатной оси Oy)
и y = 0 (уравнения координатной оси Ox).
Слайд 7 Замечание. Пусть прямая ℓ не проходит через
O(0;0).
Тогда уравнение ℓ можно записать в виде
cosα·x + cosβ·y
+ C = 0,где C = – p (доказать самим).
Этот частный случай общего уравнения прямой называется нормальным уравнением прямой.
Обозначим:
1) P0(x0;y0) – основание перпендикуляра, опущенного на ℓ из начала координат,
Слайд 8 2. Другие формы записи уравнения прямой на плоскости
1) Параметрические уравнения прямой
ЗАДАЧА 2. Записать
уравнение прямой, проходящей через точку M0(x0;y0), параллельно вектору Вектор, параллельный прямой, называют направляющим вектором этой прямой.
Слайд 9
2) Каноническое уравнение прямой на плоскости
3) Уравнение прямой,
проходящей через две точки – частный случай канонического уравнения
прямой.Пусть прямая проходит через две точки M1(x1,y1) и M2(x2,y2) .
Слайд 10
4) Уравнение прямой с угловым коэффициентом
Пусть прямая ℓ не параллельна оси Ox. Тогда она
пересекается с Ox, образуя при этом две пары вертикальных углов. Угол ϕ , отсчитываемый от оси Ox к прямой ℓ против часовой стрелки, называют углом наклона прямой ℓ к оси Ox.
Число k = tgϕ (если оно существует, т.е. если прямая ℓ не параллельна оси Oy) называют угловым коэффициентом прямой.
Для прямой, параллельной оси Ox, угол наклона прямой к оси Ox считают равным нулю. Следовательно, угловой коэффициент такой прямой k = tg0 = 0.
Слайд 11 Пусть прямая ℓ не параллельна оси Ox и
Oy и проходит через точки M1(x1,y1) и M2(x2,y2) (где
x1 < x2). Найдем угловой коэффициент этой прямой.Слайд 12 Уравнение y – y1 = k·(x – x1)
– это уравнение прямой, проходящей через точку M1(x1,y1) и
имеющей угловой коэффициент k.Перепишем это уравнение в виде y = kx + b (где b = y1 – kx1). Его называют уравнением прямой с угловым коэффициентом. С геометрической точки зрения b – отрезок, отсекаемый прямой на оси Oy.
Замечание. Уравнение прямой с угловым коэффициентом было получено в предположении, что прямая не параллельна оси Ox и Oy. Для прямой, параллельной Ox общее уравнение можно рассматривать как уравнение с угловым коэффициентом. Действительно, уравнение такой прямой
y = b или y = 0·x + b,
где k = 0 – угловой коэффициент прямой.
Слайд 13
3. Взаимное расположение прямых на плоскости
На плоскости
две прямые могут:
а) быть параллельны, б) пересекаться. Пусть уравнения прямых ℓ1 и ℓ2 имеют вид:
ℓ1: A1x + B1y + C1 = 0 или y = k1x + b1
ℓ2: A2x + B2y + C2 = 0 или y = k2x + b2
1) Пусть прямые параллельны:
Слайд 14 Получаем, что прямые ℓ1 и ℓ2 параллельны тогда
и только тогда, когда в их общих уравнениях коэффициенты
при соответствующих текущих координатах пропорциональны, т.е. или их угловые коэффициенты равны, т.е.
k1 = k2 .
Слайд 15
2) Пусть прямые пересекаются
где знак плюс берется в
том случае, когда надо найти величину острого угла, а
знак минус – когда надо найти величину тупого угла.критерий перпендикулярности прямых, заданных общими уравнениями.
Слайд 16 где знак плюс берется в том случае, когда
надо найти величину острого угла, а знак минус –
когда надо найти величину тупого угла.критерий перпендикулярности прямых, имеющий угловые коэффициенты k1 и k2.
Слайд 17
4. Расстояние от точки до прямой
ЗАДАЧА 3. Пусть
прямая ℓ задана общим уравнением
Ax + By +
C = 0 , M0(x0;y0) – точка, не принадлежащая прямой ℓ.
Найти расстояние от точки M0 до прямой ℓ .
Слайд 18 § Плоскость 1. Общее уравнение плоскости и его исследование
ЗАДАЧА 1. Записать уравнение плоскости, проходящей через точку M0(x0;y0;z0),
перпендикулярно векторуВектор, перпендикулярный плоскости, называют нормальным вектором этой плоскости.
Слайд 19
ВЫВОДЫ:
1) Плоскость является поверхностью первого порядка. В
общем случае она задается уравнением Ax+By+Cz+D=0, где A,B,C,D –
числа.2) Коэффициенты A, B, C не обращаются в ноль одновременно, так как с геометрической точки зрения это координаты вектора, перпендикулярного плоскости.
Слайд 20
ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИ
Если в уравнении Ax+By+Cz+D =
0 все коэффициенты A,B,C и D отличны от нуля,
то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – неполным.1) Пусть общее уравнение плоскости – полное. Тогда его можно записать в виде
С геометрической точки зрения a,b и c – отрезки, отсекаемые плоскостью на координатных осях Ox, Oy и Oz соответственно. Уравнение (3) называют уравнением плоскости в отрезках.
Слайд 21 2) Пусть в общем уравнении плоскости коэффициенты A,
B и C – ненулевые, а D = 0,
т.е. уравнение плоскости имеет видAx+By +Cz = 0.
Такая плоскость проходит через начало координат O(0;0;0).
ℓ1: By+Cz = 0 (пересечение с плоскостью Oyz)
ℓ2: Ax+By = 0 (пересечение с плоскостью Oxy)
Слайд 22 а) плоскость отсекает на осях Ox и Oy
отрезки a и b соответственно и параллельна оси Oz;
3)
Пусть в общем уравнении плоскости один из коэффициентов A, B или C – нулевой, а D ≠ 0, т.е. уравнение плоскости один из следующих трех видов:а) Ax+By+D = 0 б) Ax+Cz+D = 0 в) By+Cz+D = 0.
Эти уравнения можно записать соответственно в виде
Слайд 23 б) плоскость отсекает на осях Ox и Oz
отрезки a и c соответственно и параллельна оси Oy;
в)
плоскость отсекает на осях Oy и Oz отрезки b и c соответственно и параллельна оси Ox.Иначе говоря, плоскость, в уравнении которой отсутствует одна из координат, параллельна оси отсутствующей координаты.
Слайд 24 4) Пусть в уравнении плоскости (2) два из
трех коэффициентов A, B или C – нулевые, а D
≠ 0, т.е. уравнение плоскости имеет вид: а) Ax+D = 0 или б) By+D = 0 или в) Cz+D = 0.Эти уравнения можно записать соответственно в виде:
а) плоскость отсекает на оси Ox отрезок a и параллельна осям Oy и Oz (т.е. параллельна плоскости Oyz);
Слайд 25 б) плоскость отсекает на Oy отрезок b и
параллельна осям Ox и Oz (т.е. параллельна плоскости Oxz);
в)
плоскость отсекает на Oz отрезок c и параллельна осям Ox и Oy (т.е. параллельна плоскости Oxy).Иначе говоря, плоскость, в уравнении которой отсутствуют две координаты, параллельна координатной плоскости, проходящей через оси отсутствующих координат.
Слайд 26 5) Пусть в общем уравнении плоскости (2) D
= 0 и один из коэффициентов A, B или
C тоже нулевой, т.е. уравнение плоскости имеет вид:а) Ax+By = 0 или б) Ax+Cz = 0 или в) By+Cz = 0.
Плоскость проходит через начало координат и ось отсутствующей координаты
Слайд 27 6) Пусть в общем уравнении плоскости (2) три
коэффициента равны нулю, т.е. уравнение плоскости имеет вид
а)
Ax = 0 или б) By = 0 или в) Cz = 0.Эти уравнения можно записать соответственно в виде:
а) x = 0 – уравнение координатной плоскости Oyz;
б) y = 0 – уравнение координатной плоскости Oxz,
в) z = 0 – уравнение координатной плоскости Oxy.
Слайд 28
Замечание. Пусть плоскость λ не проходит через O(0;0;0).
Тогда
уравнение λ можно записать в виде
cosα · x +
cosβ · y + cosγ · z + D = 0,где D = – p (доказать самим).
Этот частный случай общего уравнения плоскости называется нормальным уравнением плоскости.
Обозначим:
1) P0(x0;y0;z0) – основание перпендикуляра, опущенного на λ из начала координат,
Слайд 29
2. Другие формы записи уравнения плоскости
1) Уравнение плоскости,
проходящей через точку
параллельно двум неколлинеарным векторам
ЗАДАЧА 2. Записать уравнение плоскости, проходящей через точку M0(x0;y0;z0), параллельно неколлинеарным векторам
Другие формы записи:
Уравнение плоскости, проходящей через точку перпендикулярно вектору (см. уравнение (1) и (1*));
Уравнение плоскости в отрезках (см уравнение (2));
Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам;
Уравнение плоскости, проходящей через три точки;
Слайд 31 2) Уравнение плоскости, проходящей через три точки, не
лежащие на одной прямой – частный случай уравнения
(4)Пусть плоскость проходит через три точки M1(x1;y1;z1), M2(x2;y2;z2) и M3(x3;y3;z3), не лежащие на одной прямой.
Слайд 32
3. Взаимное расположение плоскостей
В пространстве две плоскости
могут:
а) быть параллельны, б) пересекаться. Пусть уравнения плоскостей λ1 и λ2 имеют вид:
λ1: A1x + B1y + C1z + D1 = 0
λ2: A2x + B2y + C2z + D2 = 0
Тогда:
Слайд 33
1) Пусть плоскости параллельны:
Получаем, что плоскости λ1 и
λ2 параллельны тогда и только тогда, когда в их
общих уравнениях коэффициенты при соответствующих неизвестных пропорциональны, т.е.
Слайд 34
2) Пусть плоскости пересекаются
где знак плюс берется в
том случае, когда надо найти величину острого угла, а
знак минус – когда надо найти величину тупого угла.
Слайд 35
Частный случай – плоскости перпендикулярны, т.е.
критерий перпендикулярности плоскостей,
заданных общими уравнениями.
Слайд 36
4. Расстояние от точки до плоскости
ЗАДАЧА 3. Пусть
плоскость λ задана общим уравнением
Ax + By +
Cz + D = 0 , M0(x0;y0;z0) – точка, не принадлежащая плоскости λ .
Найти расстояние от точки M0 до плоскости λ .
Слайд 37 § Прямая в пространстве 1. Уравнения прямой в пространстве
Пусть A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 – уравнения любых двух
различных плоскостей, содержащих прямую ℓ . Тогда координаты любой точки прямой ℓ удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы Систему (1) называют общими уравнениями прямой в пространстве.
Слайд 38 Другие формы записи уравнений прямой в пространстве –
ПАРАМЕТРИЧЕСКИЕ и КАНОНИЧЕСКИЕ уравнения.
ЗАДАЧА 1. Записать уравнение прямой в
пространстве, проходящей через точку M0(x0;y0;z0) , параллельно вектору Вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
Слайд 39 называют параметрическими уравнениями прямой в пространстве (в векторной
и координатной форме соответственно).
Слайд 40 Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ, ПРОХОДЯЩЕЙ
ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ.
Пусть прямая проходит через точки
M1(x1,y1,z1) и M2(x2,y2 ,z2) .Слайд 41 2. Переход от общих уравнений прямой к каноническим
Пусть прямая ℓ задана общими уравнениями:
Чтобы записать канонические
(параметрические) уравнения этой прямой, необходимо найти ее направляющий вектор и координаты какой-нибудь точки M0(x0;y0;z0) на прямой. а) Координаты точки M0 – это одно из решений системы (1).
б) Направляющий вектор
Слайд 42
3. Взаимное расположение прямых в пространстве
В пространстве
две прямые могут:
а) быть параллельны,
б) пересекаться, в) скрещиваться.Пусть прямые ℓ1 и ℓ2 заданы каноническими уравнениями:
1) Пусть прямые ℓ1 и ℓ2 параллельны:
Слайд 43
2) Пусть прямые ℓ1 и ℓ2 пересекаются:
Получили: прямые
ℓ1 и ℓ2 пересекаются ⇔ они не параллельны и
для них выполняется условиеили, в координатной форме,
3) Если для прямых ℓ1 и ℓ2 не выполняется условие (6) и (7) ((7*)), то прямые скрещиваются.
Слайд 44
4. Задачи, связанные с возможным взаимным расположением прямых
Возможное
расположение прямых в пространстве приводит к следующим задачам:
1) параллельные
прямые → расстояние между прямыми(т.е. расстояние от точки до прямой)?
2) пересекающиеся прямые → а) угол между прямыми?
б) точка пересечения прямых?
3) скрещивающиеся прямые → а) угол между прямыми?
б) расстояние между прямыми?
Слайд 45 ЗАДАЧА 2. Найти угол между пересекающимися (скрещивающимися) прямыми
в пространстве.
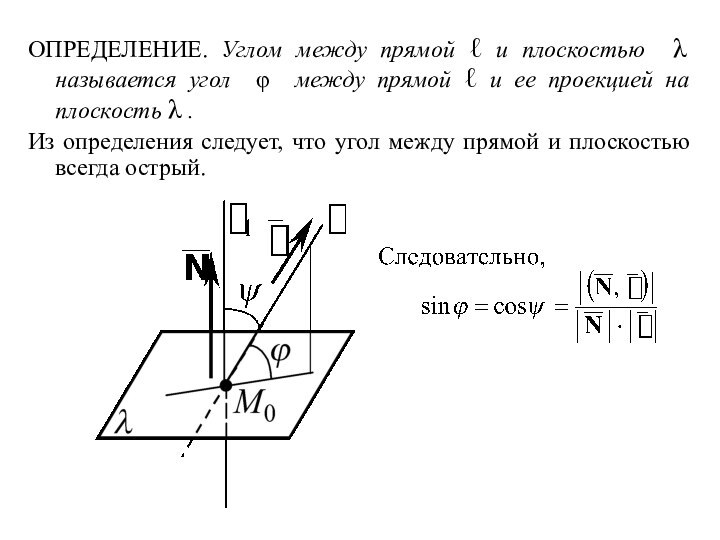
ОПРЕДЕЛЕНИЕ. Углом между двумя скрещивающимися прямыми ℓ1 и
ℓ2 называется угол между прямой ℓ1 и проекцией прямой ℓ2 на любую плоскость, проходящую через прямую ℓ1 . Т.е., угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным.
Получаем:
где знак плюс берется для острого угла, а знак минус – для тупого.
Слайд 47
ЗАДАЧА 4. Найти расстояние между скрещивающимися прямыми.
ОПРЕДЕЛЕНИЕ. Расстоянием между двумя скрещивающимися прямыми называется длина их
общего перпендикуляра. где Ax + By + Cz + D = 0 – общее уравнение плоскости λ ,
M2(x2; y2; z2) – любая точка на прямой ℓ2 .
Слайд 49
ЗАДАЧА 5. Найти точку пересечения прямых.
Пусть M0(x0;y0;z0)
– точка пересечения прямых. Тогда (x0;y0;z0) – решение системы
уравненийСлайд 50 5. Взаимное расположение прямой и плоскости в пространстве
Пусть в пространстве заданы плоскость λ и прямая ℓ
. Они могут 1) быть параллельны;2) прямая может лежать в плоскости;
3) прямая и плоскость могут пересекаться в одной точке.
Слайд 51 а) Если прямая параллельна плоскости или прямая принадлежит плоскости,
то
Если условие (10) (условие (11)) не выполняется, то
прямая и плоскость пересекаются в одной точке. б) Если прямая принадлежит плоскости, то координаты любой ее точки удовлетворяют уравнению плоскости, и, следовательно, кроме условия (10) ((11)) выполняется условие
Ax0 + By0 + Cz0 + D = 0 ,
где M0(x0;y0;z0) – любая точка прямой.





























