точек на прямой
1.2 Взаимное расположение точки и отрезка, лежащих
на одной прямой1.3 Взаимное расположение прямой и точки вне прямой
1.4 Взаимное расположение прямой и двух точек вне прямой
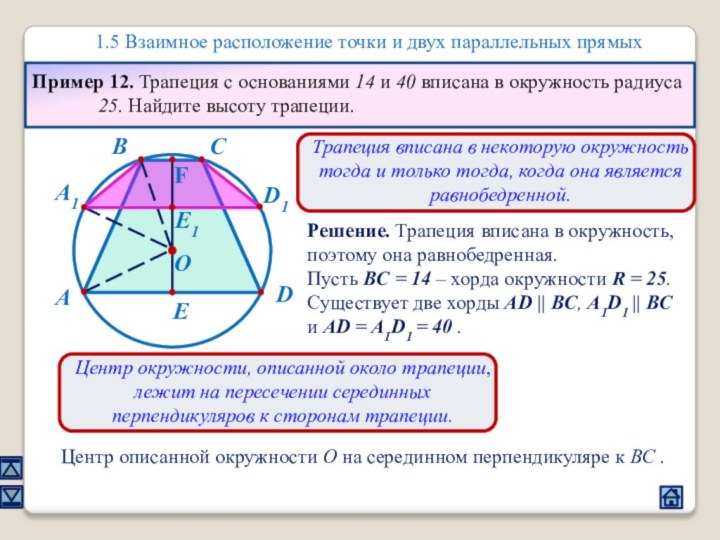
1.5 Взаимное расположение точки и двух параллельных прямых
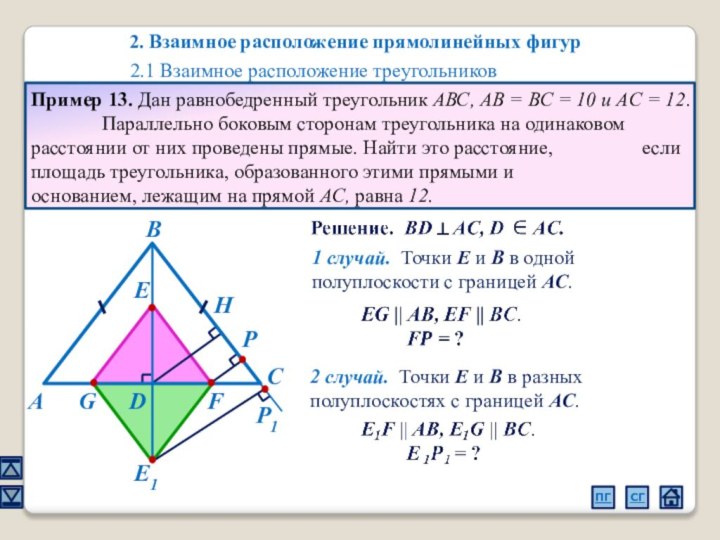
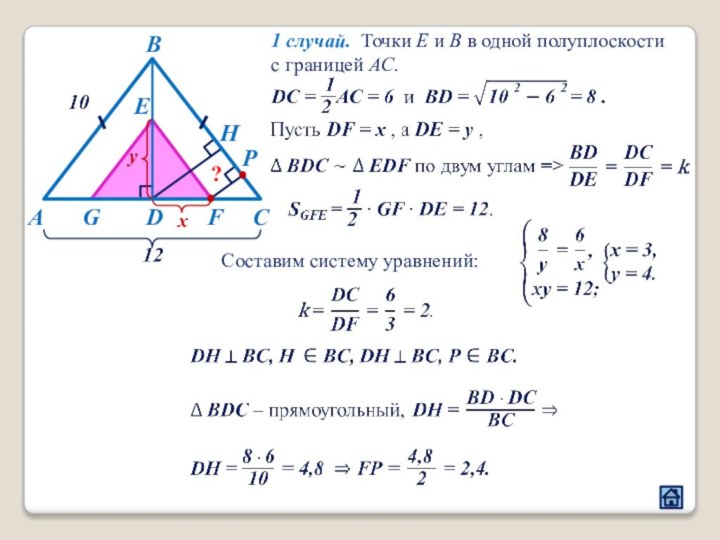
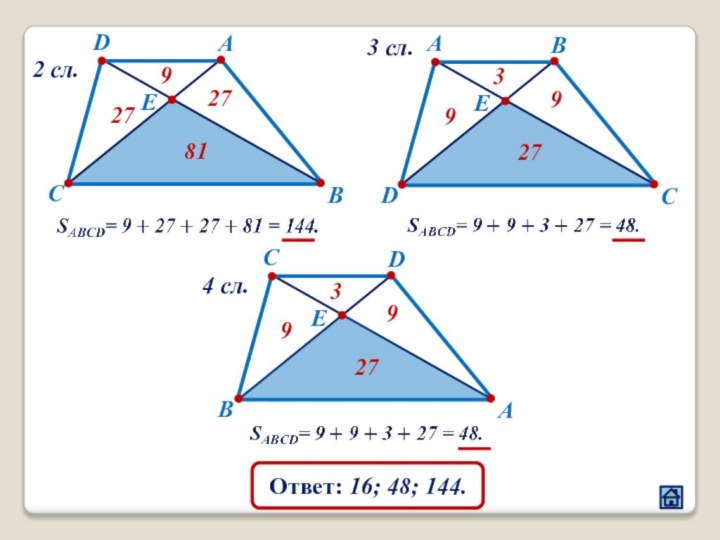
2. Взаимное расположение прямолинейных фигур
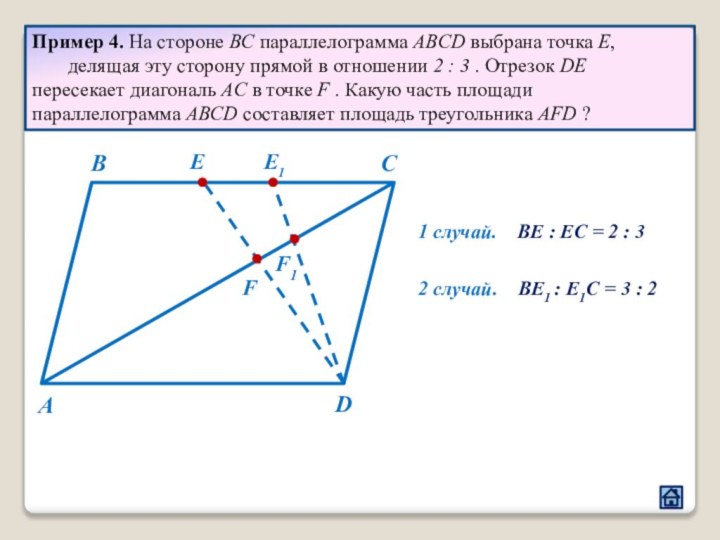
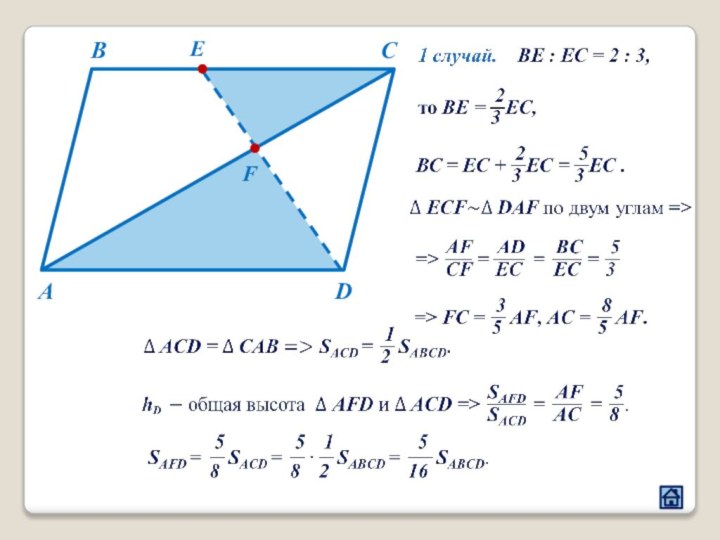
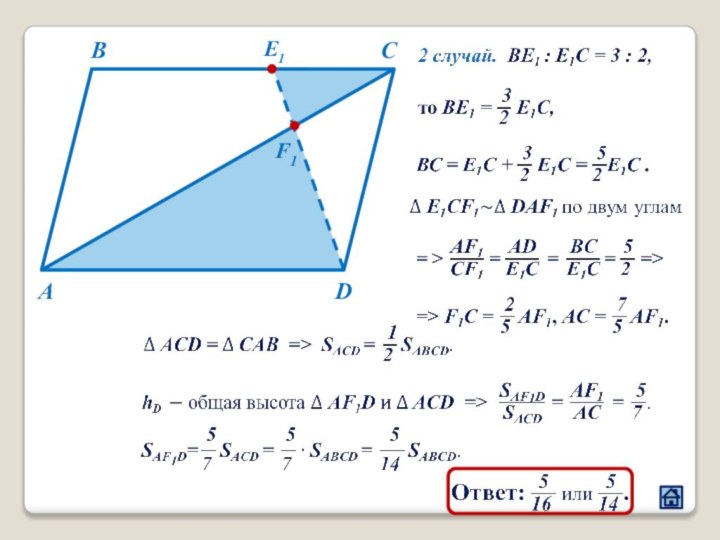
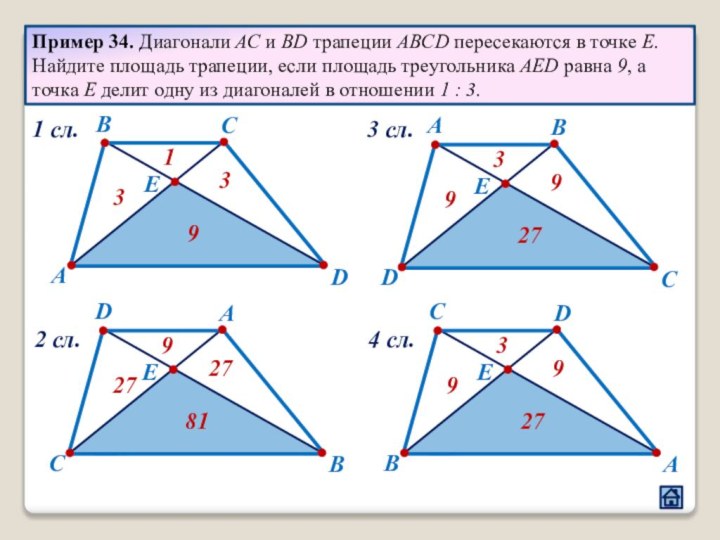
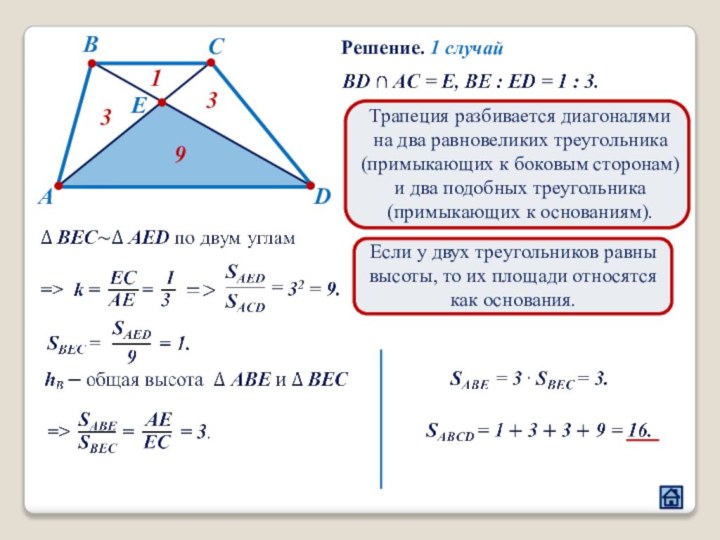
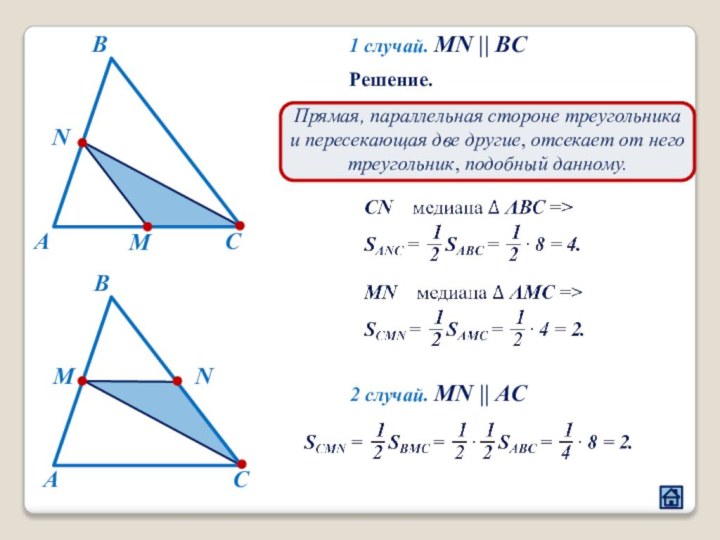
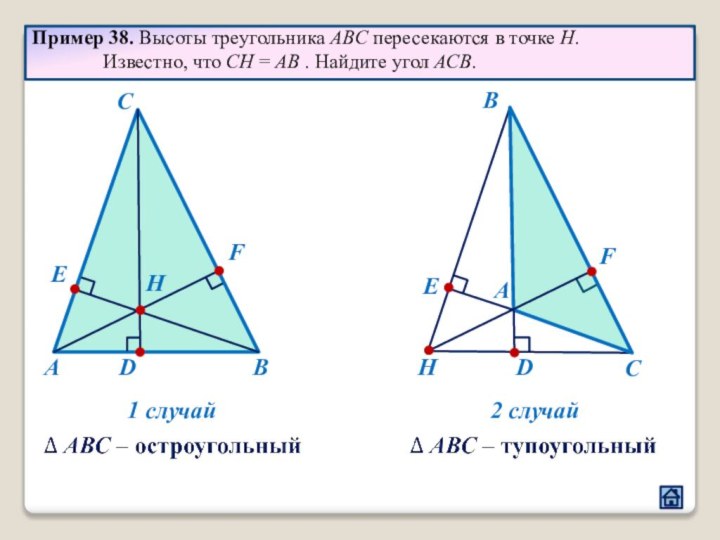
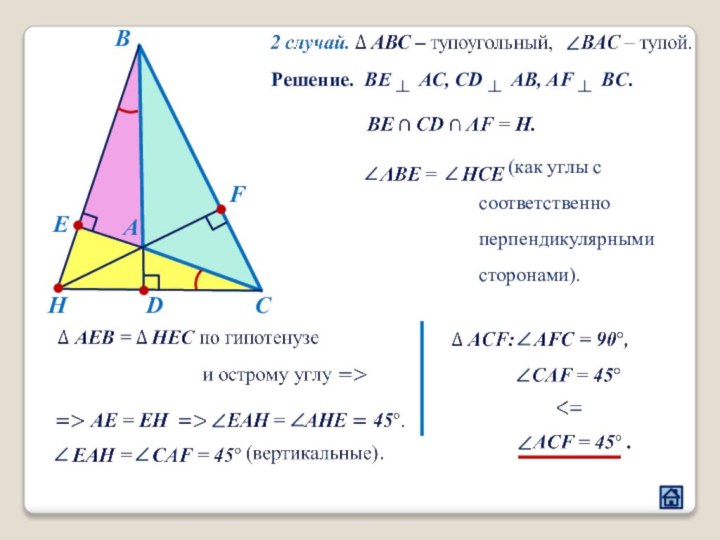
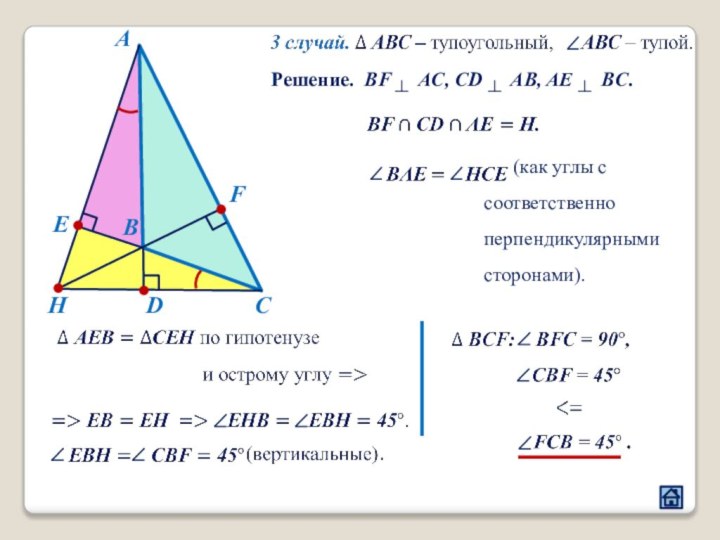
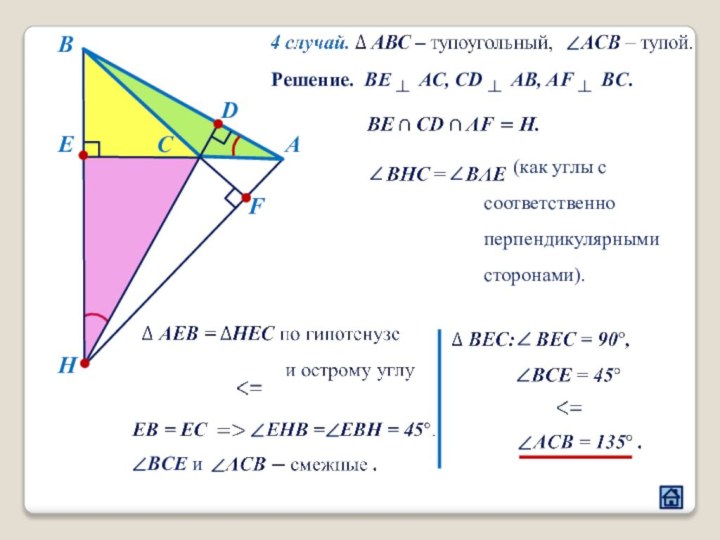
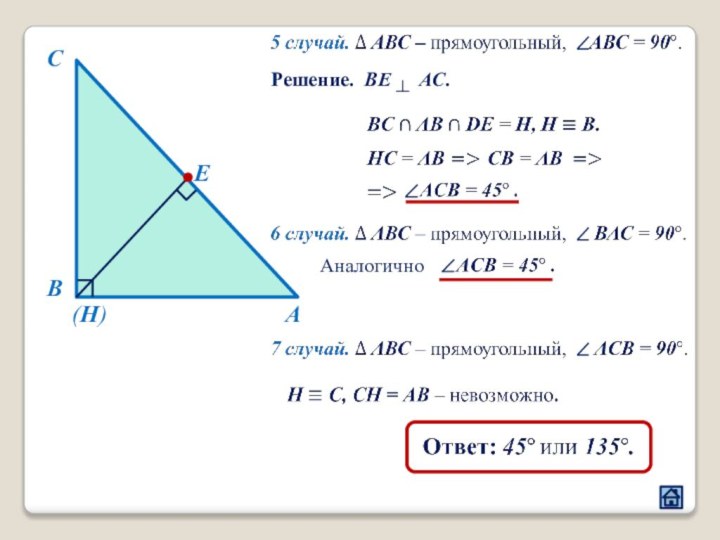
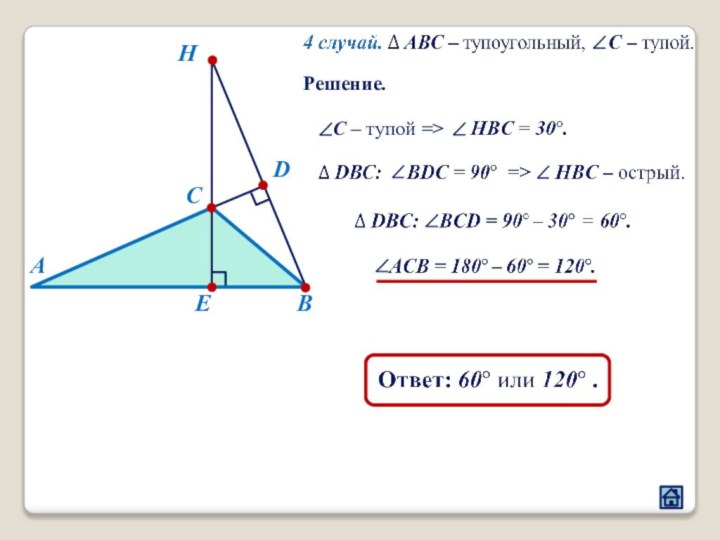
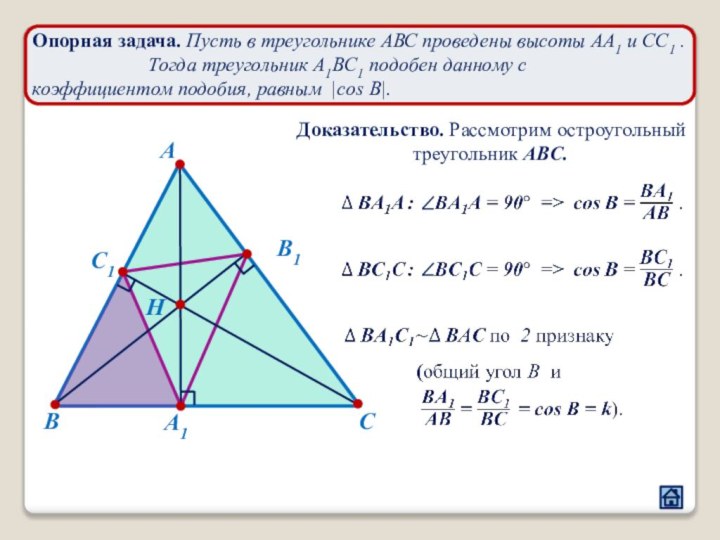
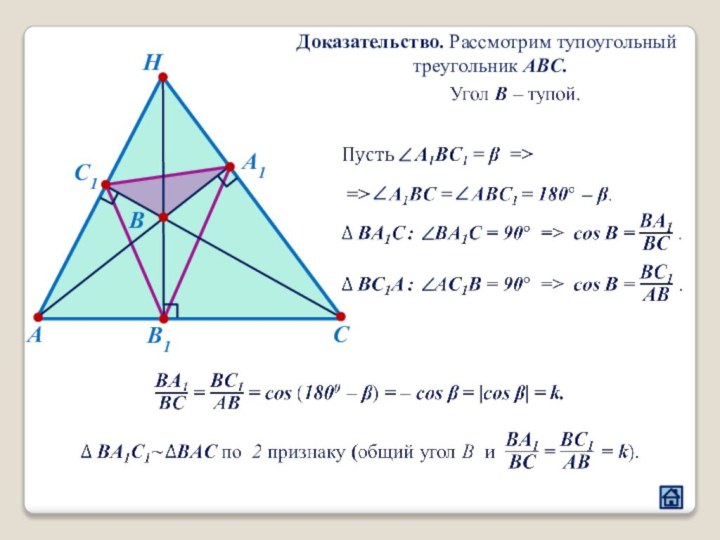
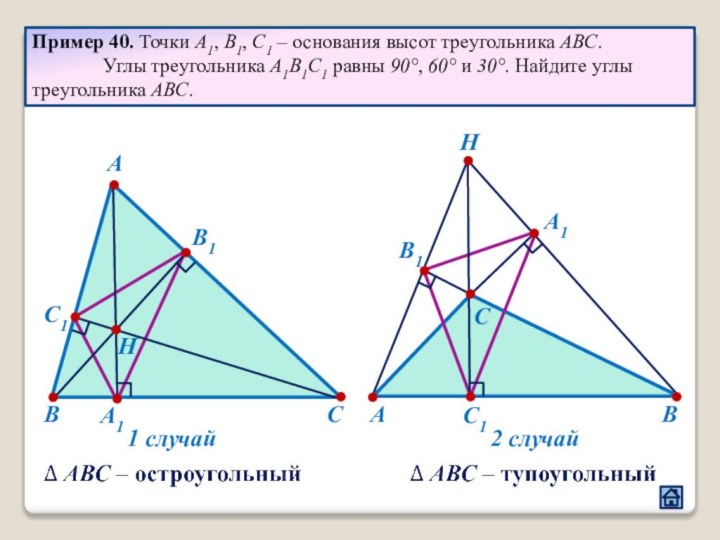
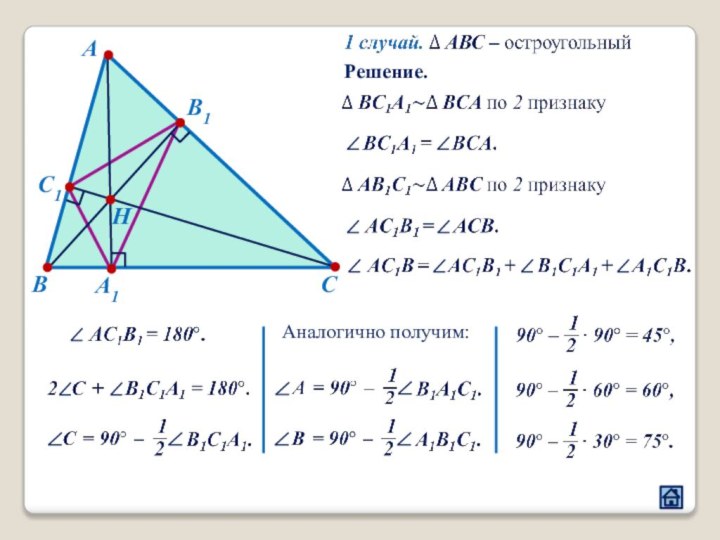
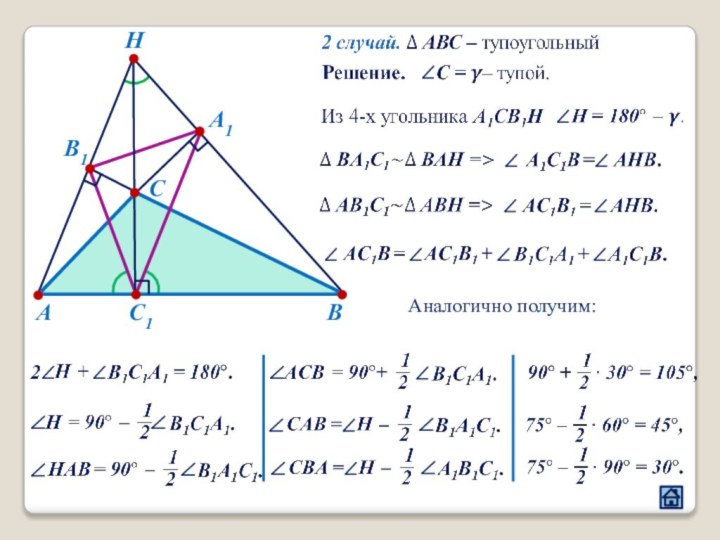
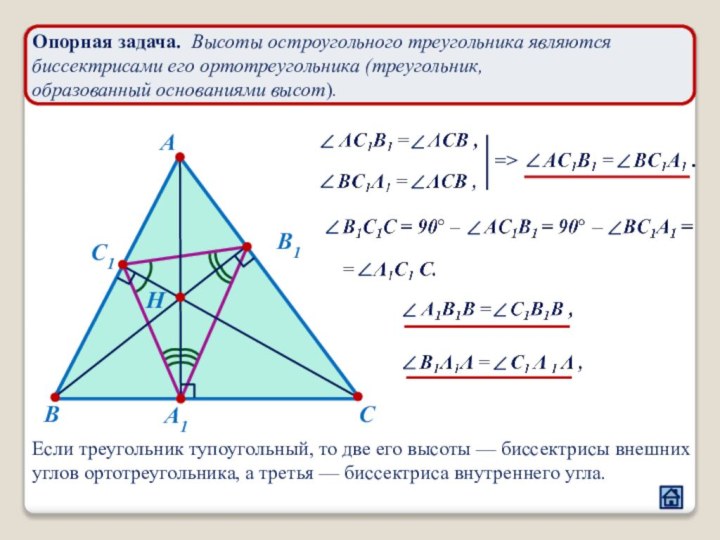
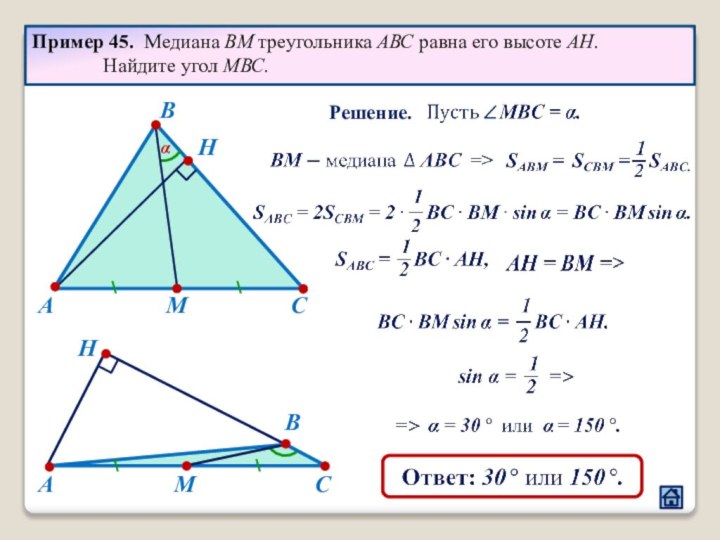
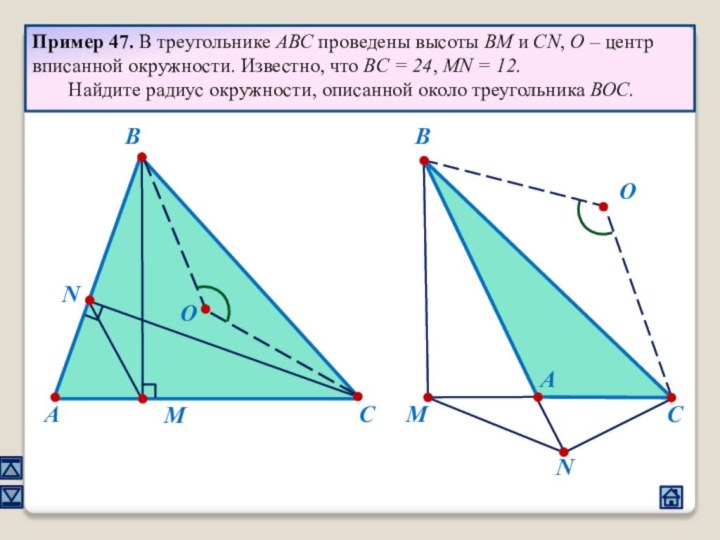
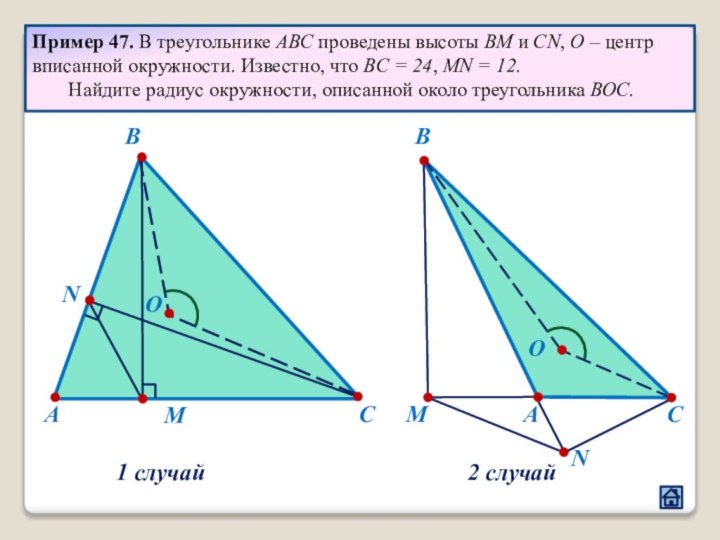
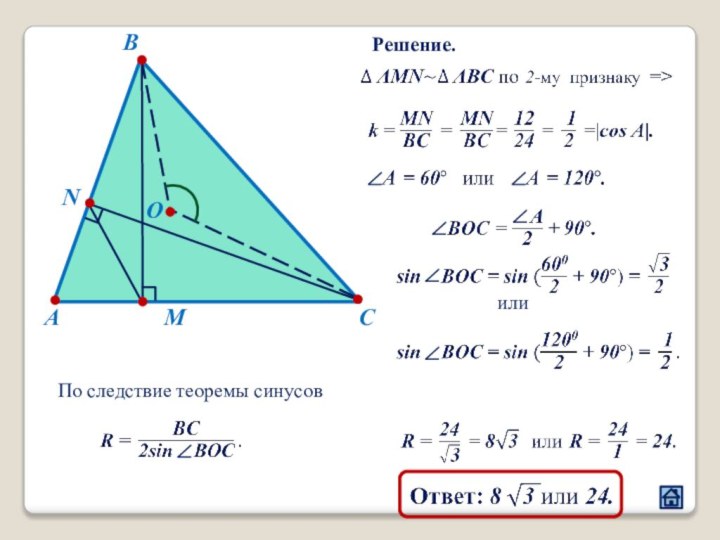
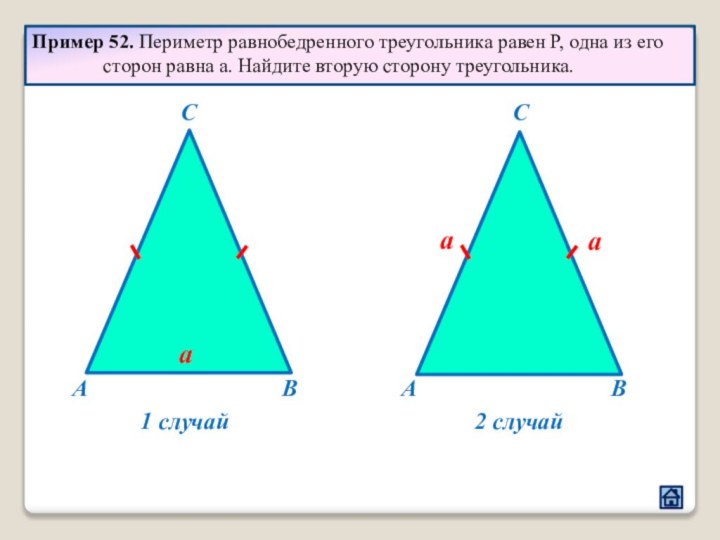
2.1 Взаимное расположение треугольников
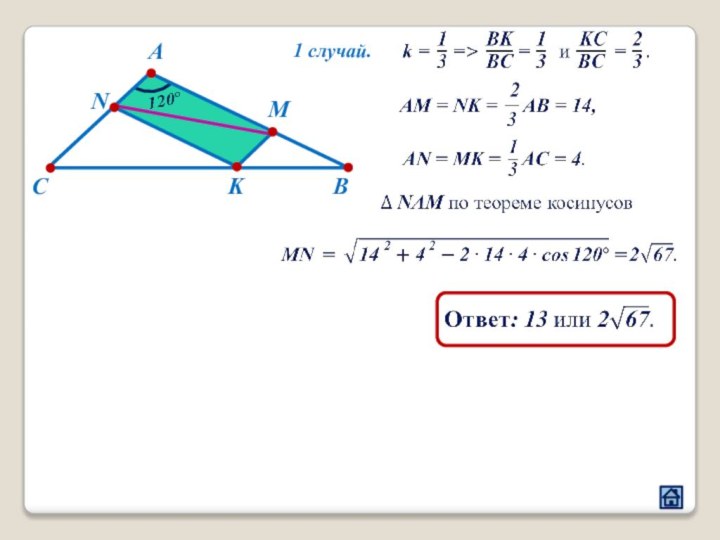
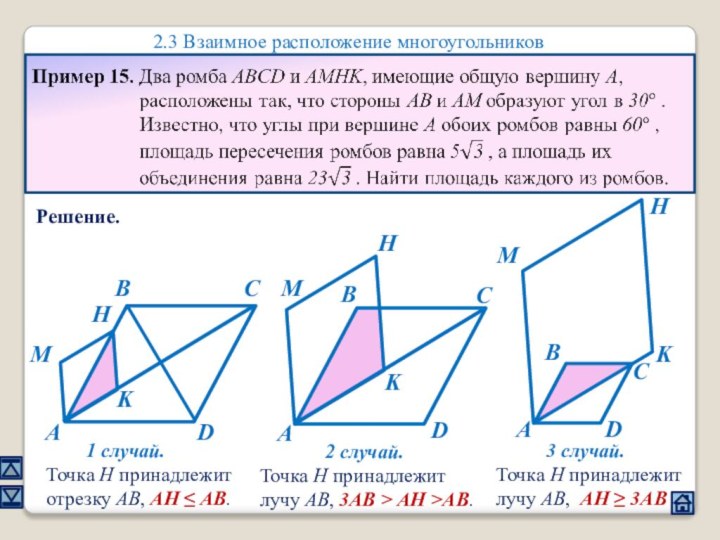
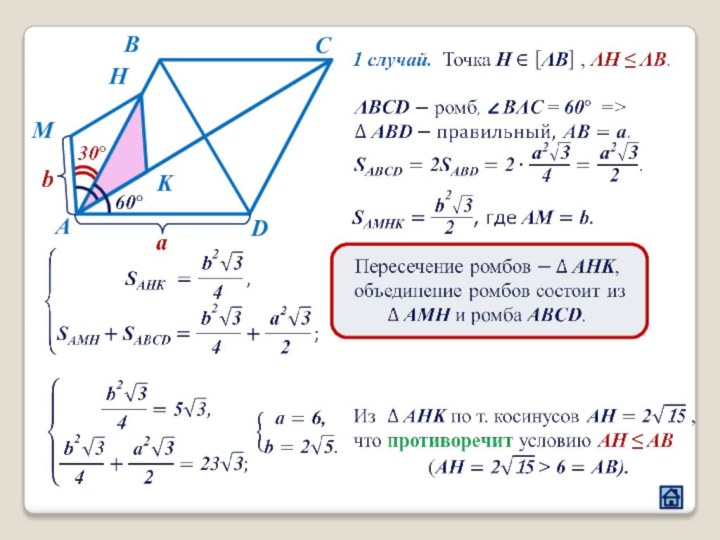
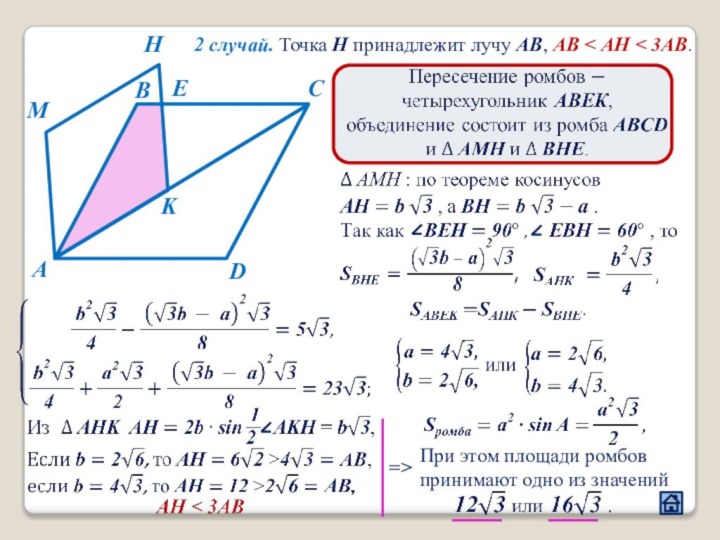
2.3 Взаимное расположение многоугольников
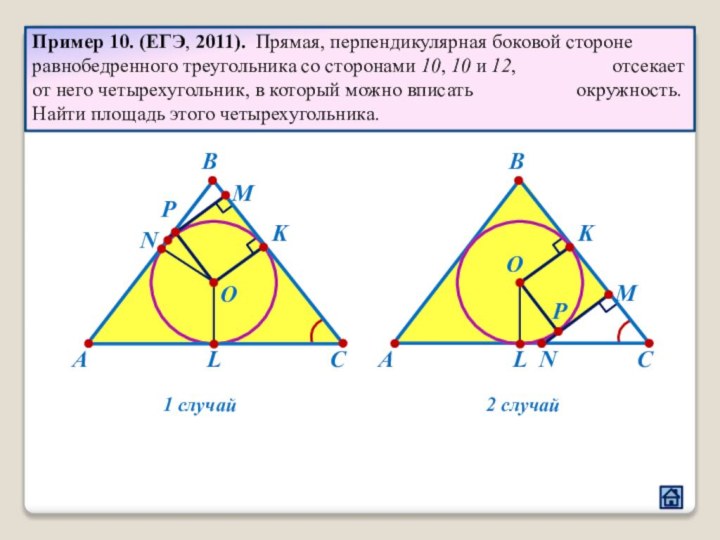
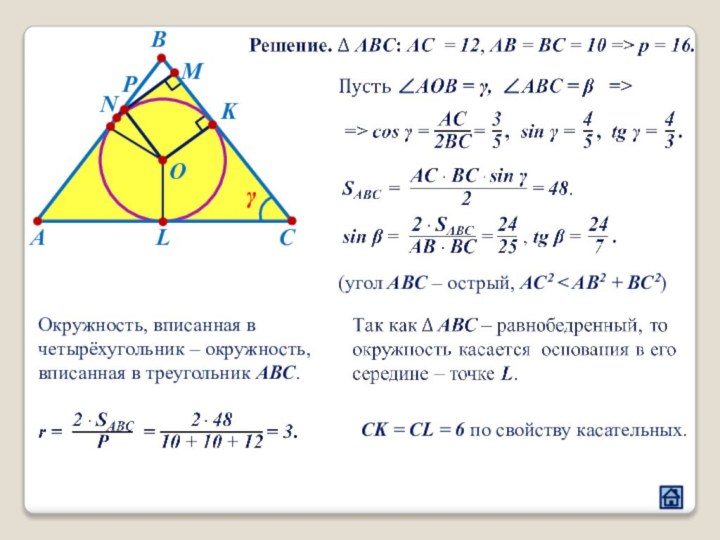
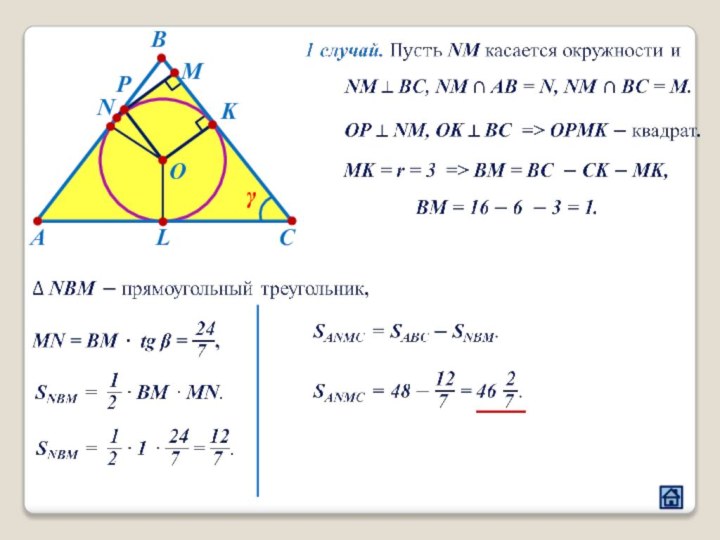
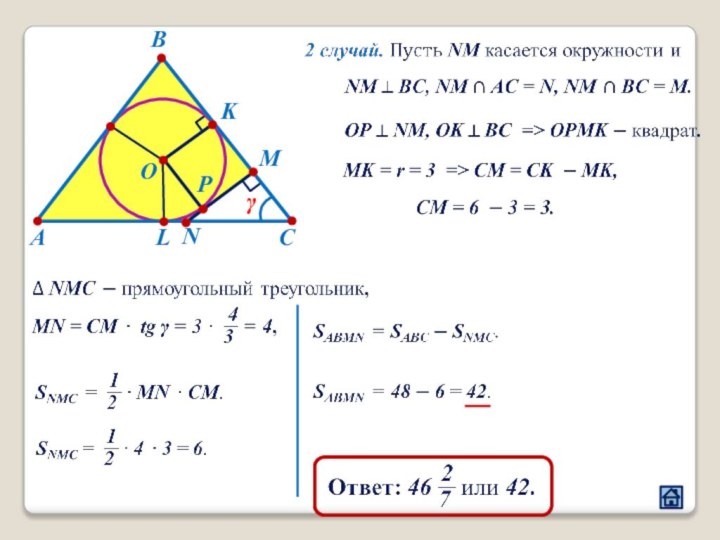
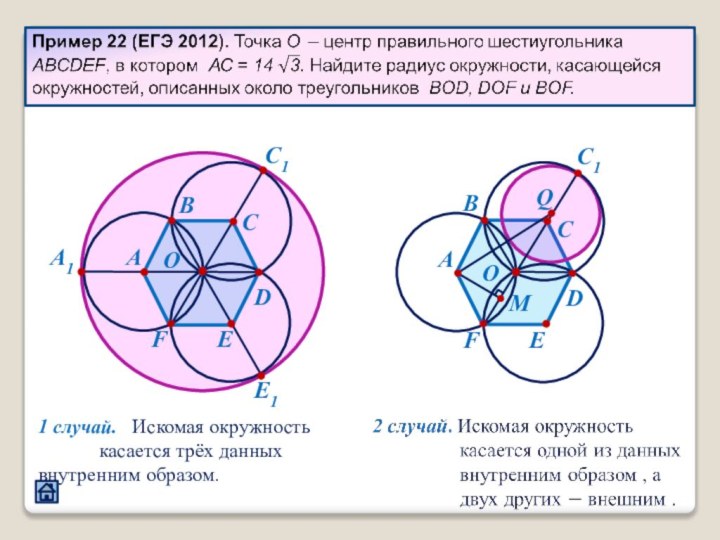
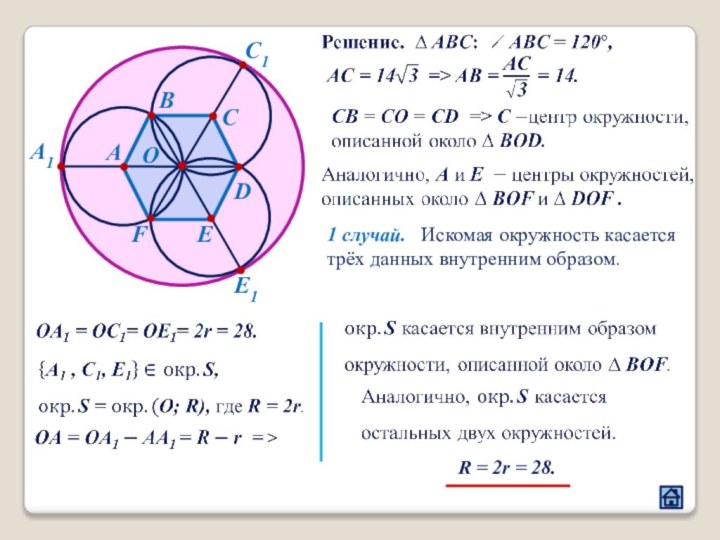
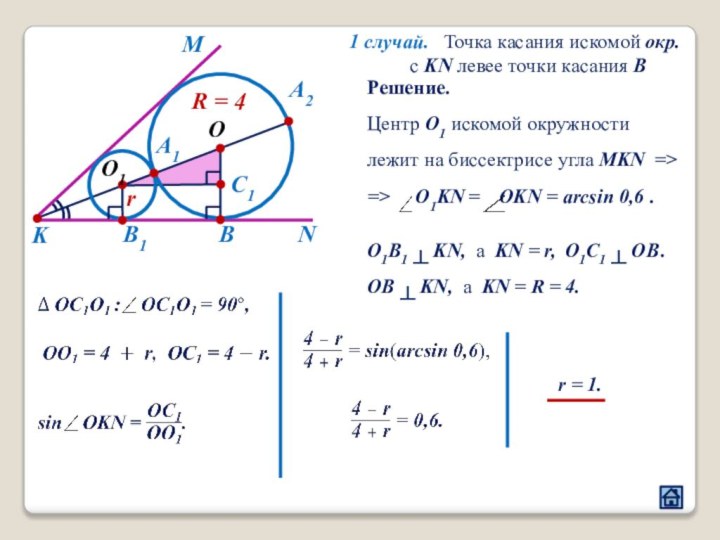
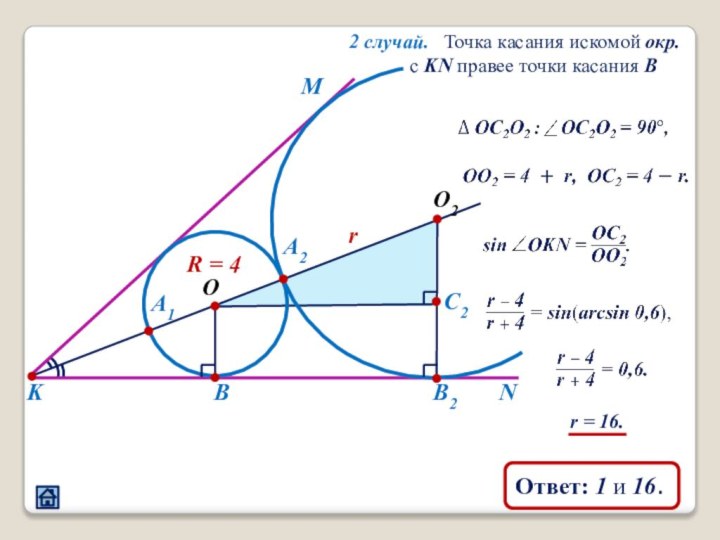
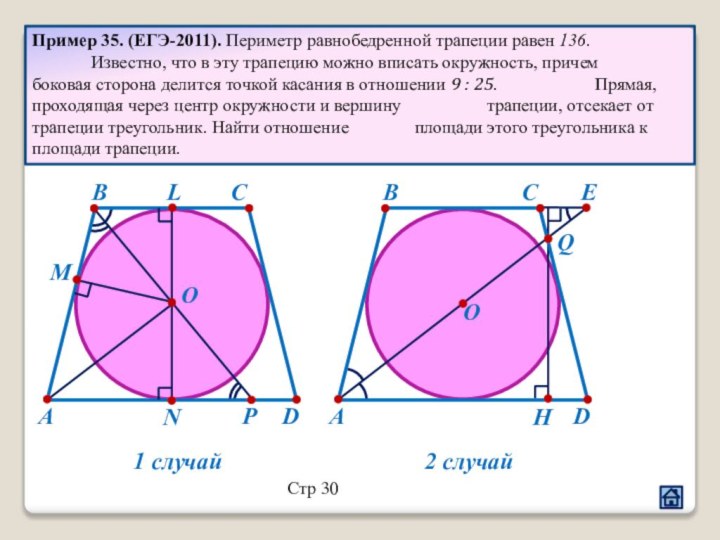
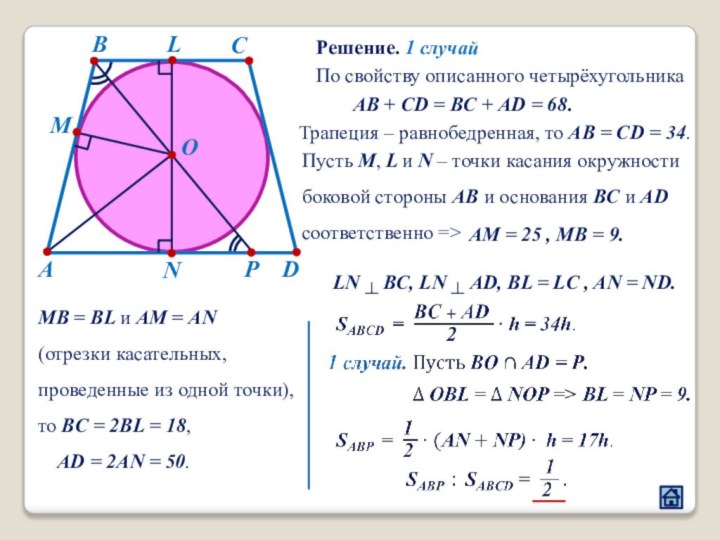
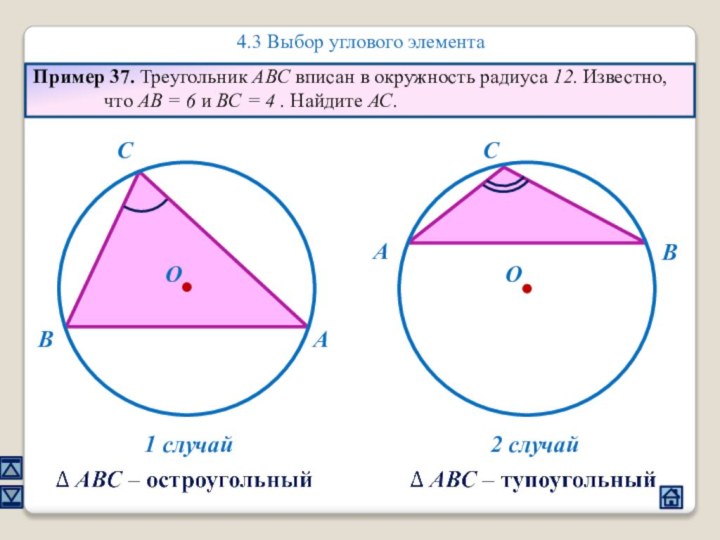
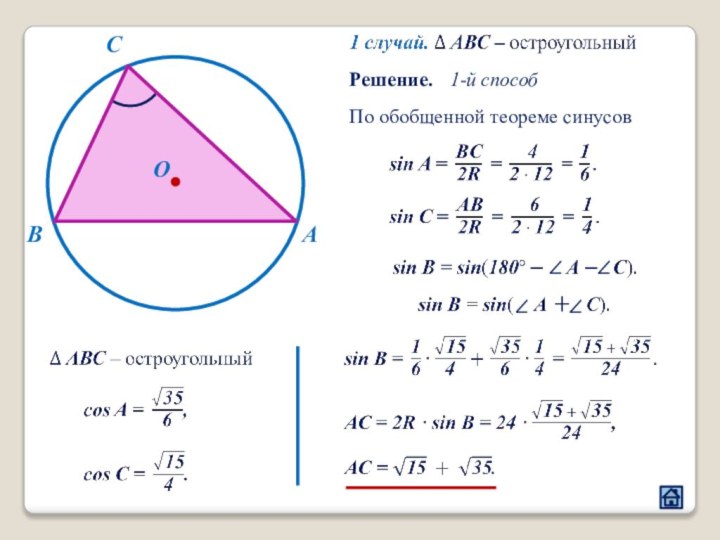
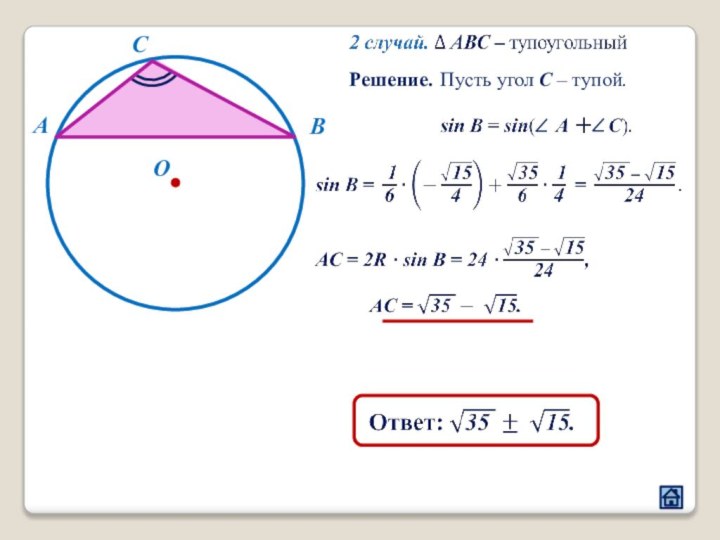
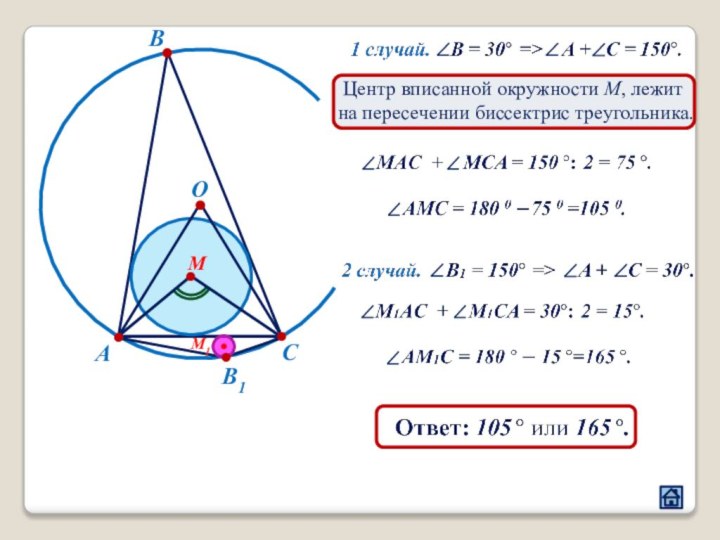
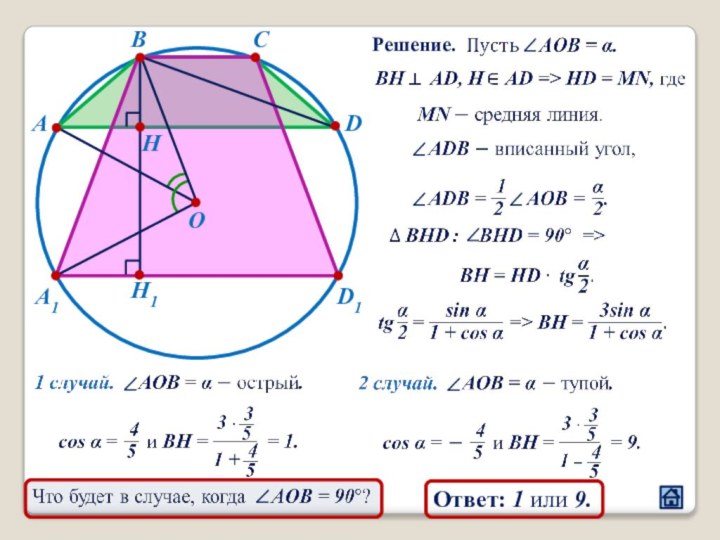
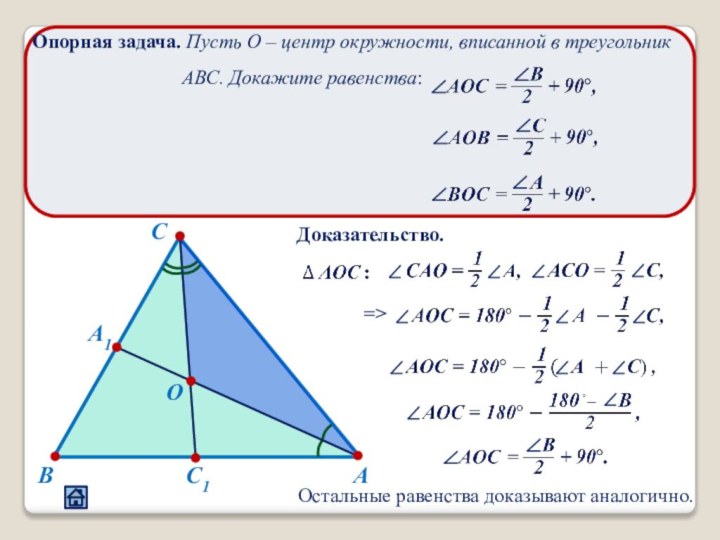
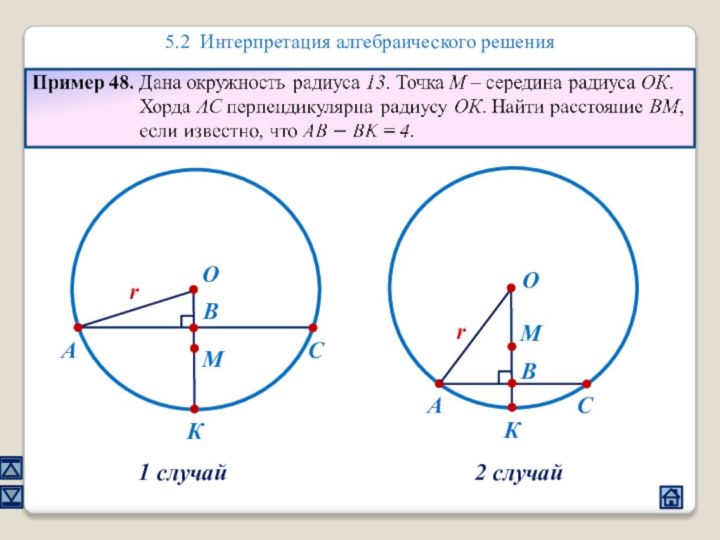
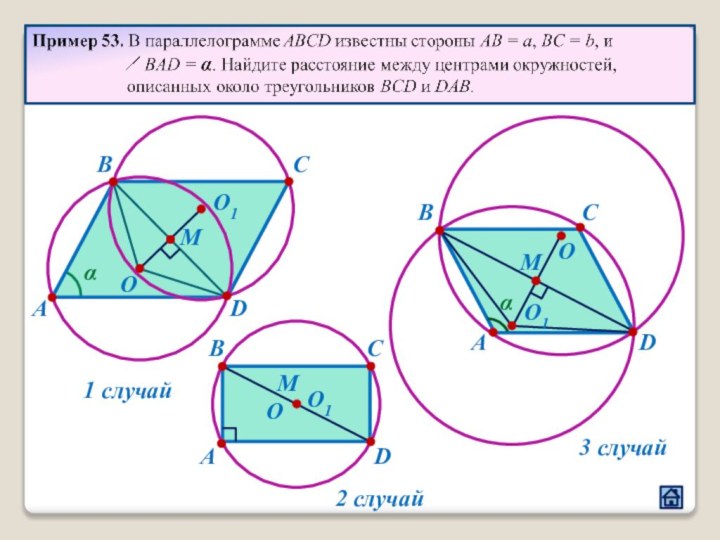
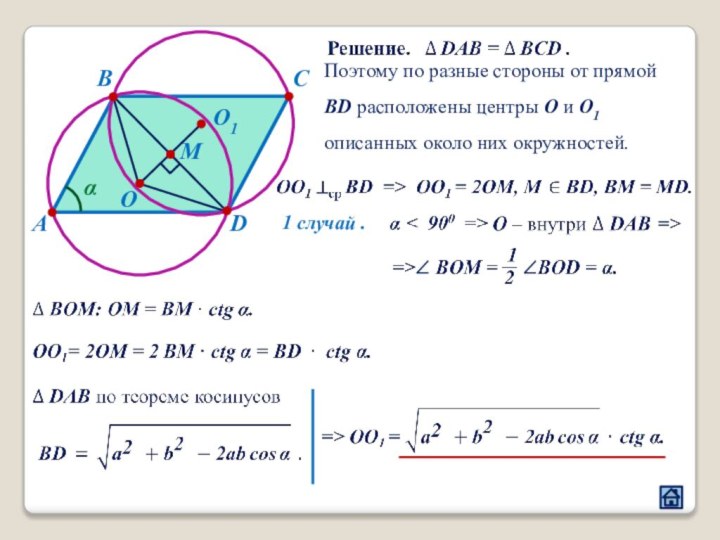
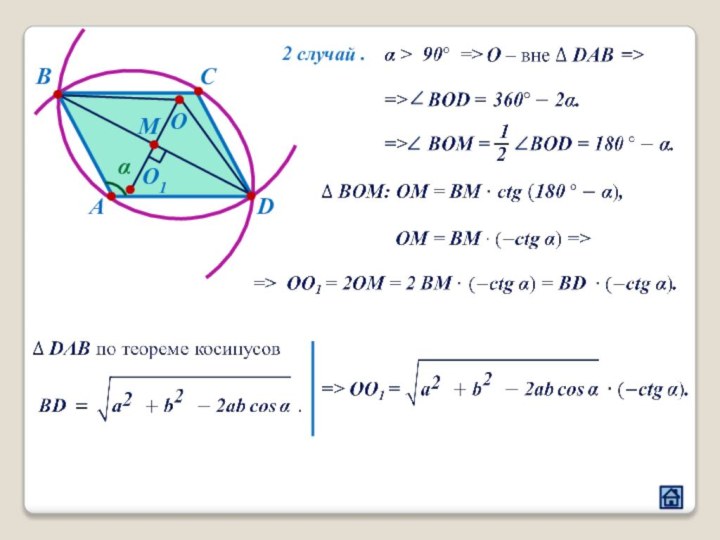
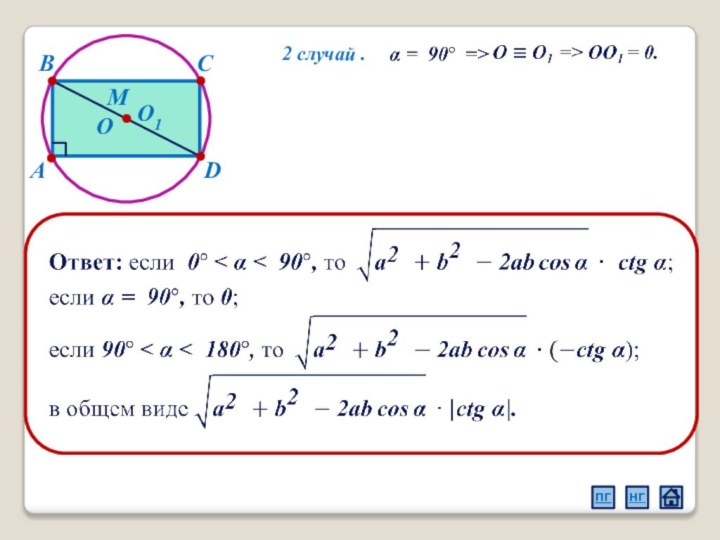
2.4 Взаимное расположение треугольника и окружности
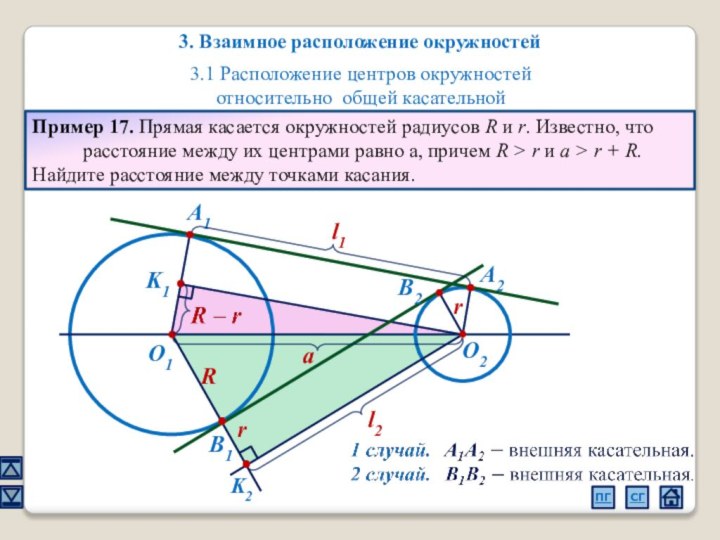
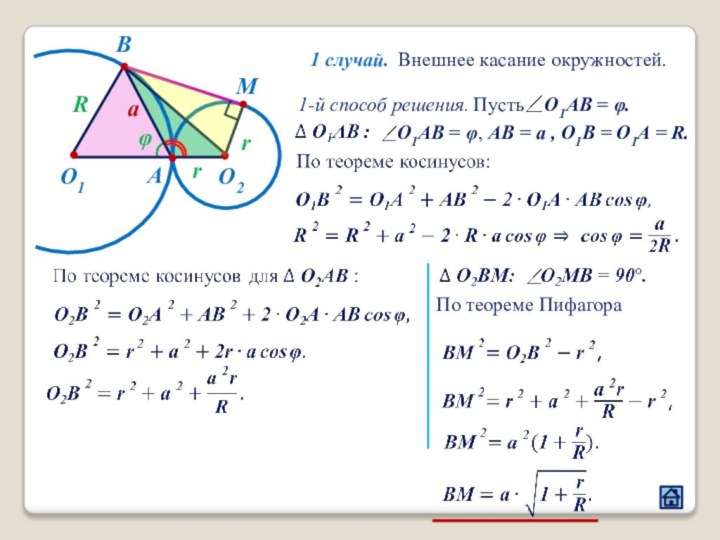
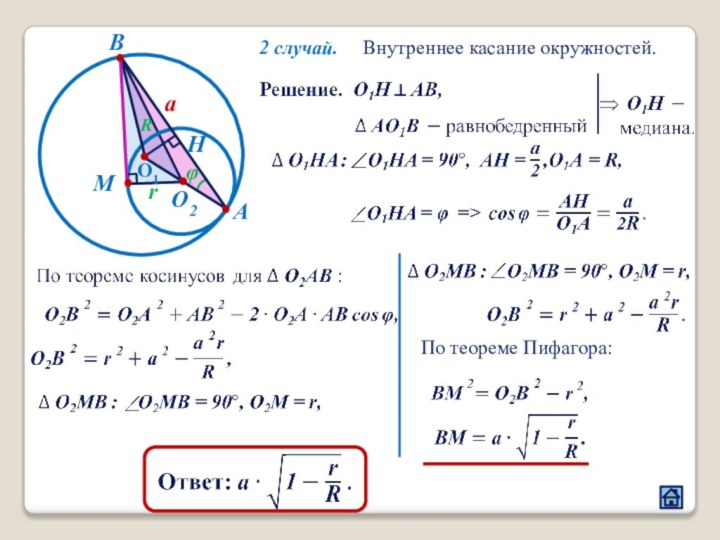
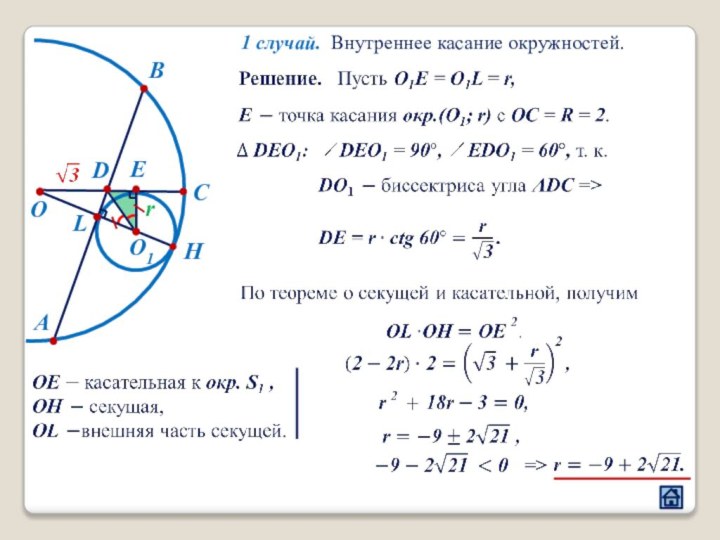
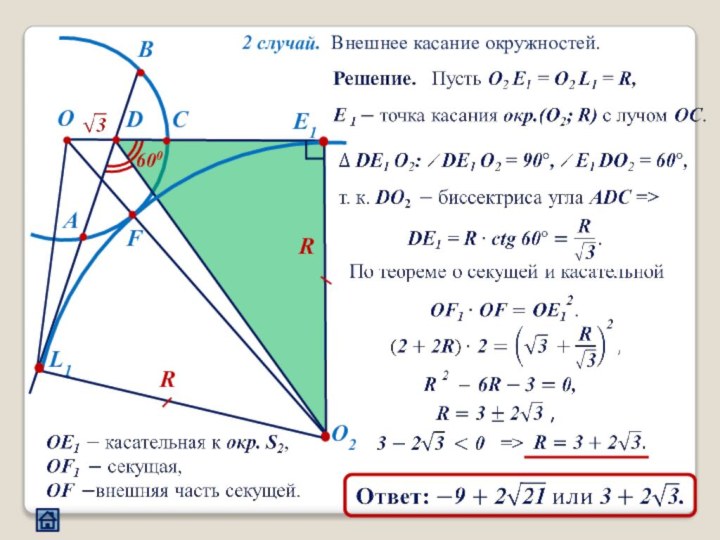
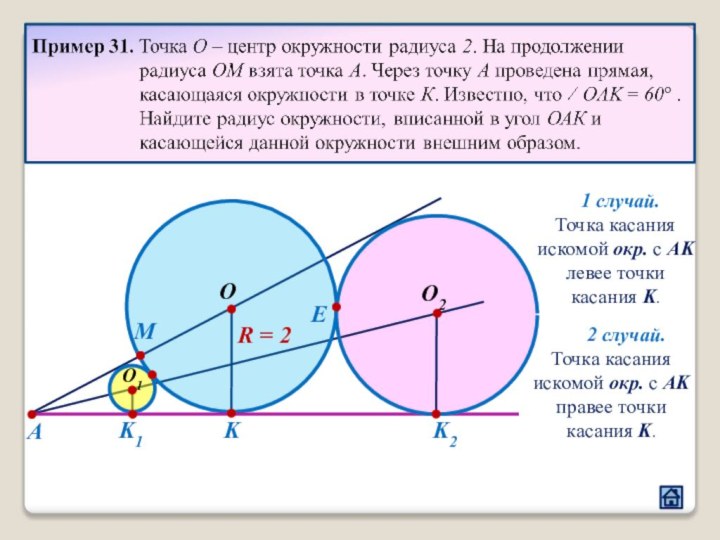
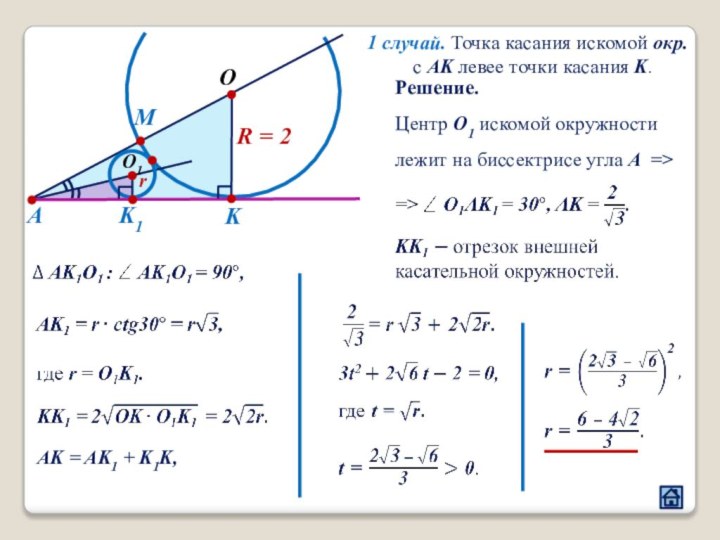
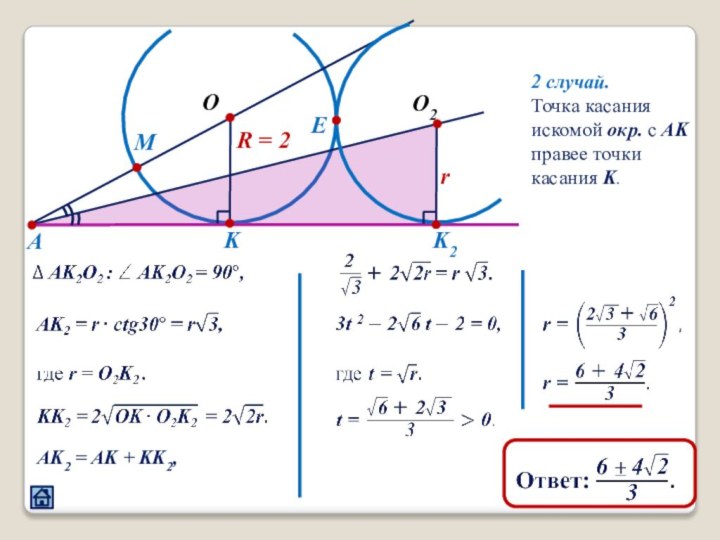
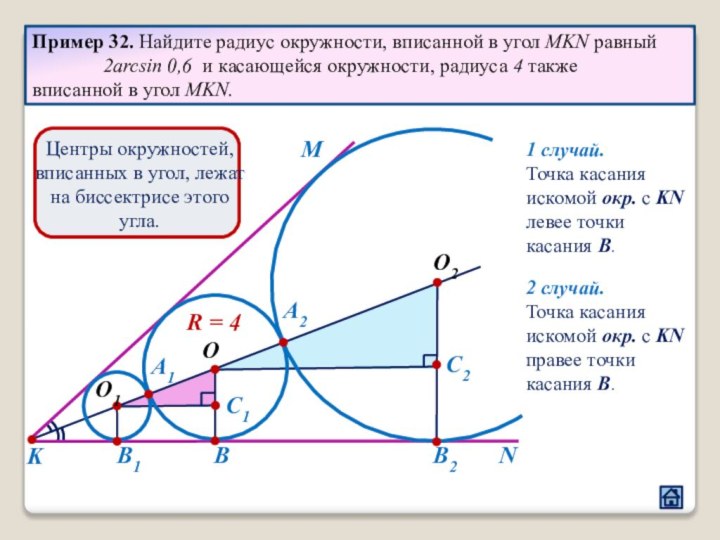
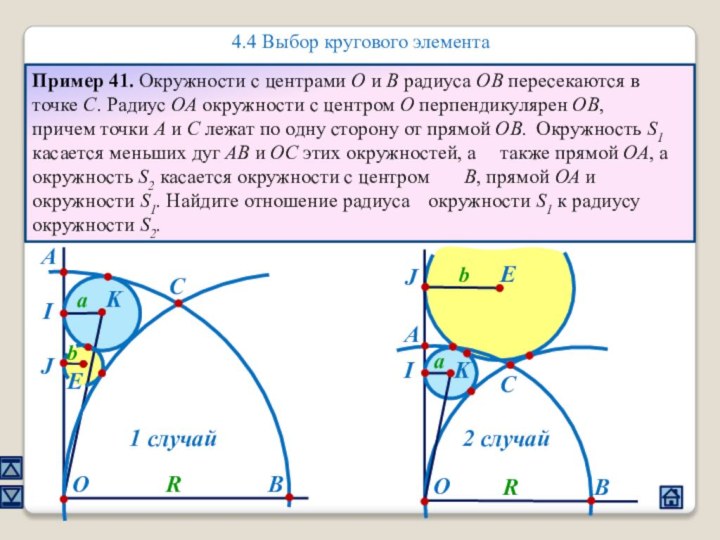
3. Взаимное расположение окружностей
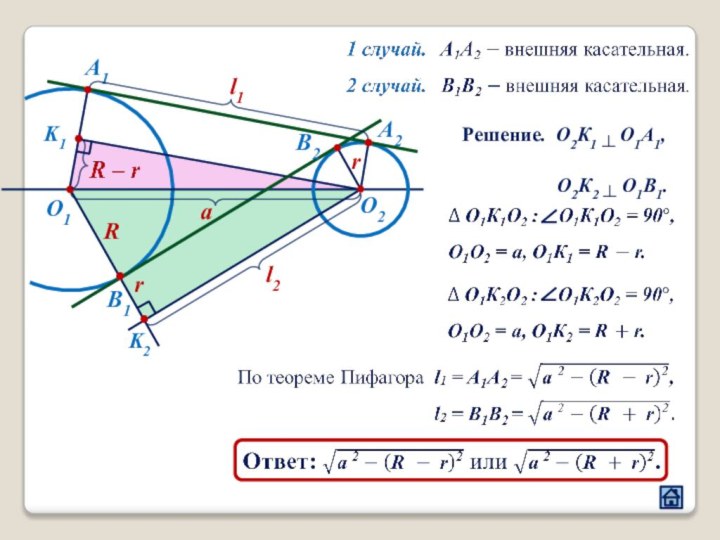
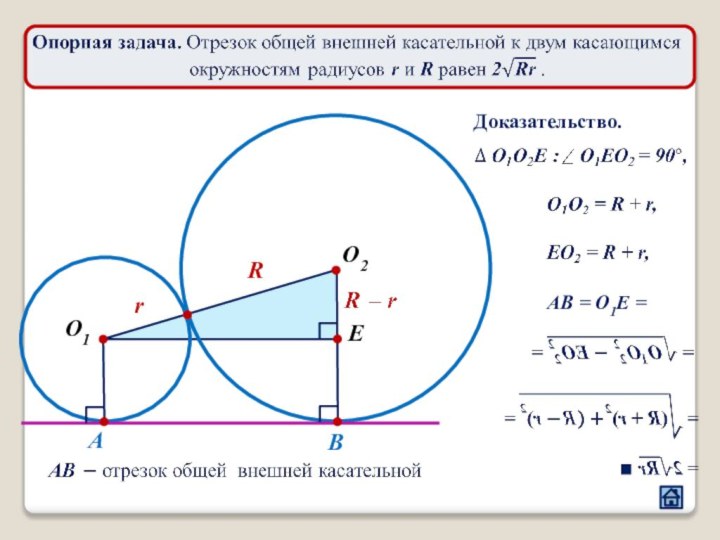
3.1 Расположение центров окружностей относительно общей касательной
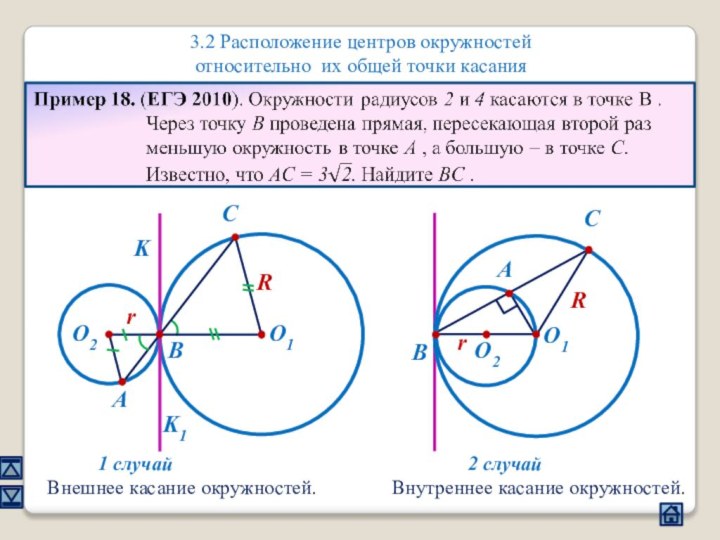
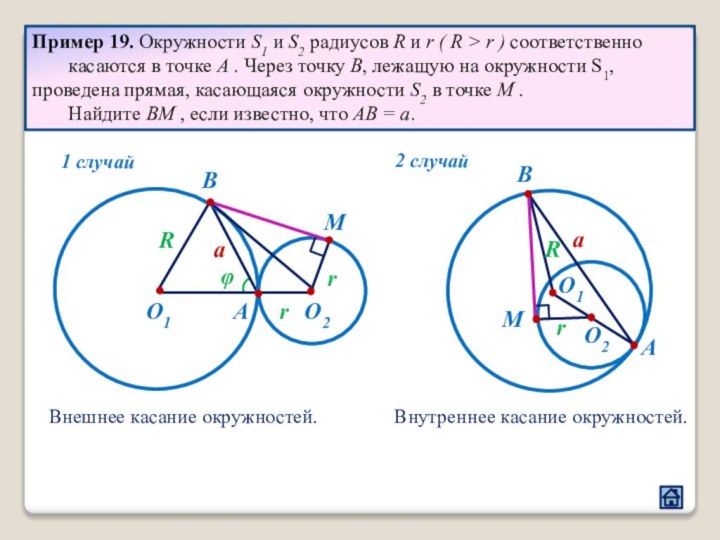
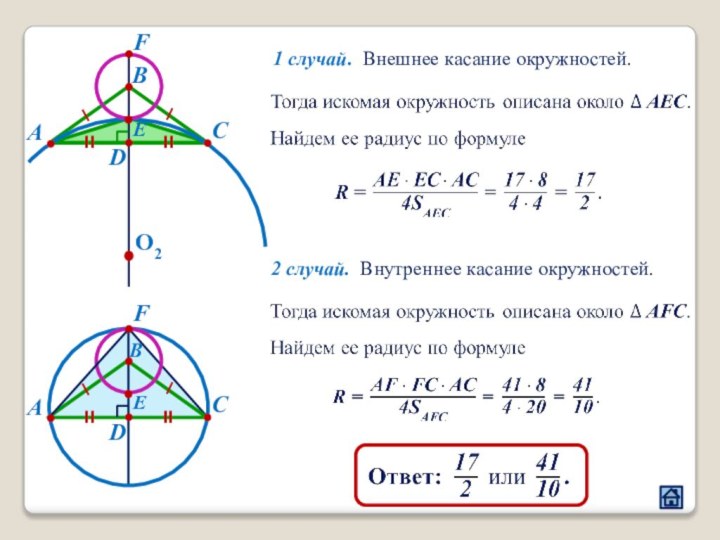
3.2 Расположение центров окружностей относительно их общей точки касания
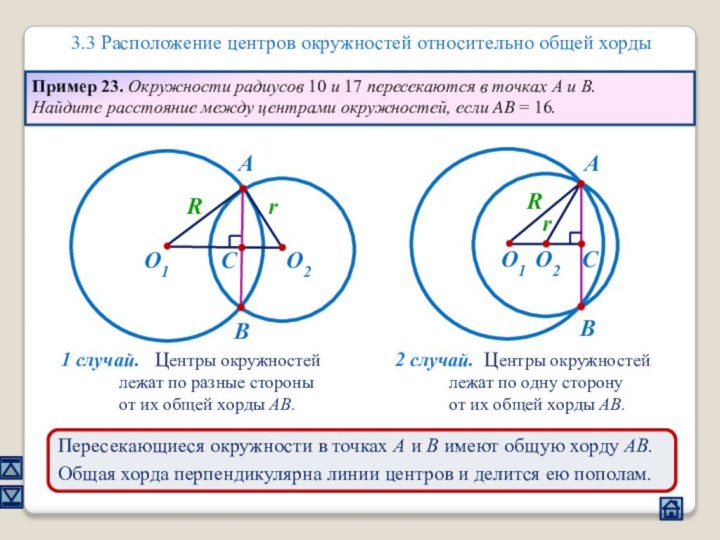
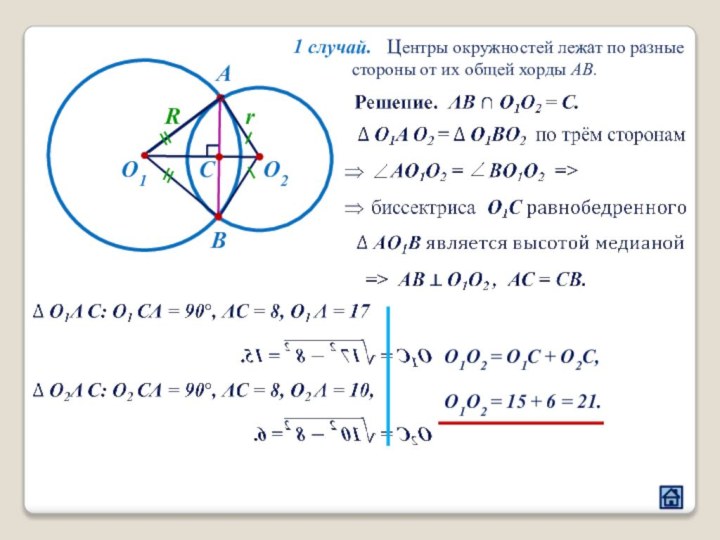
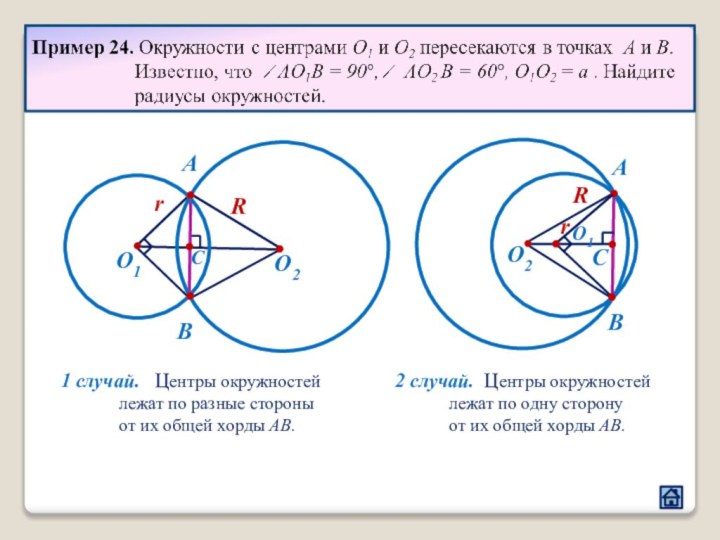
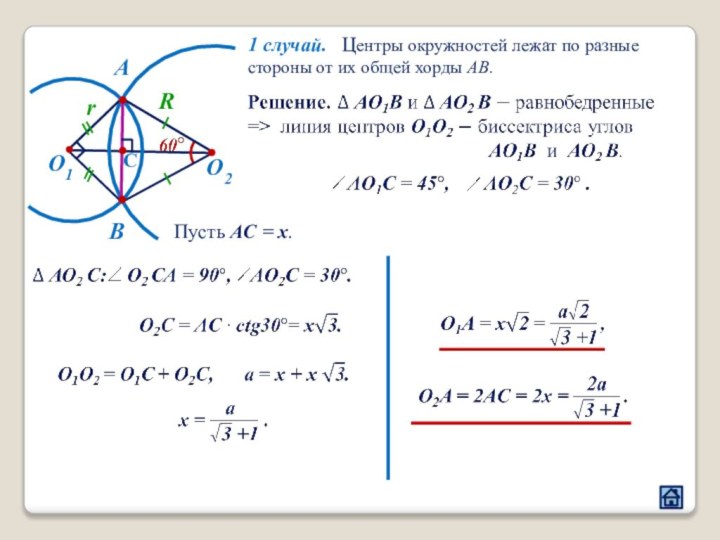
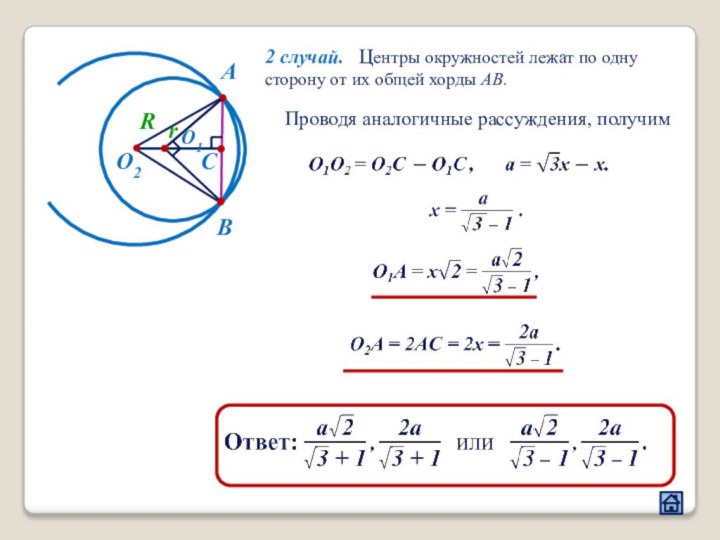
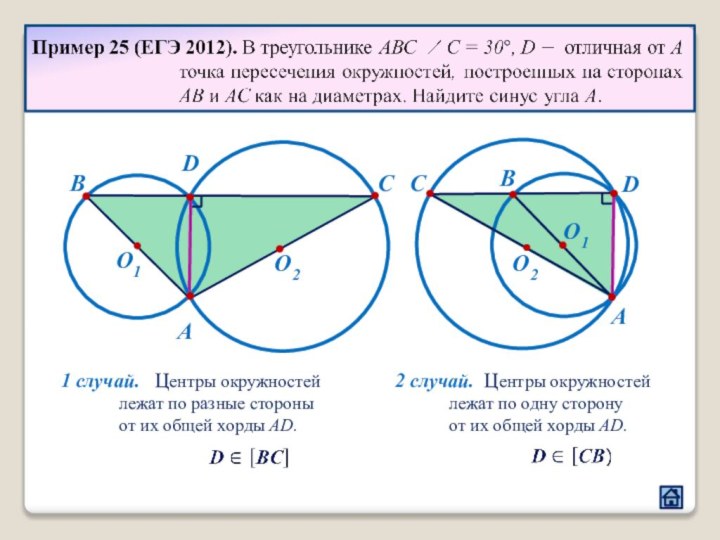
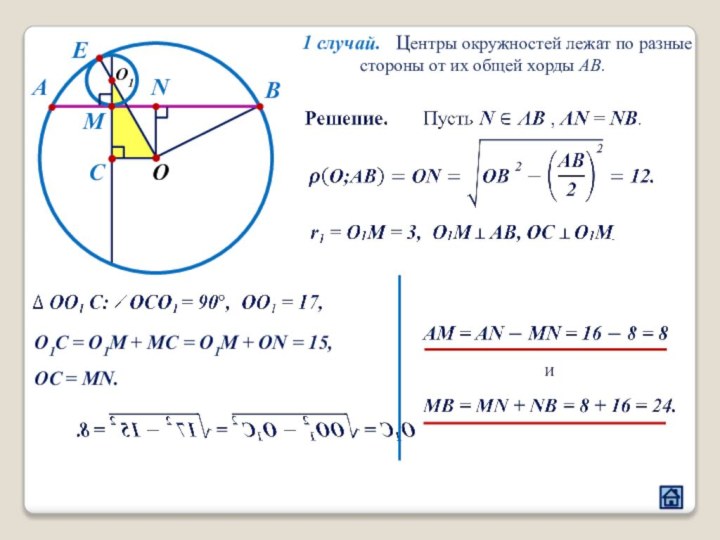
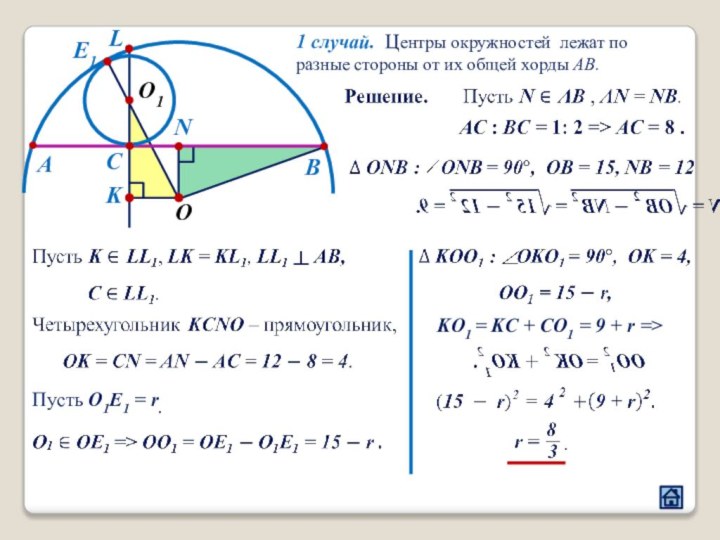
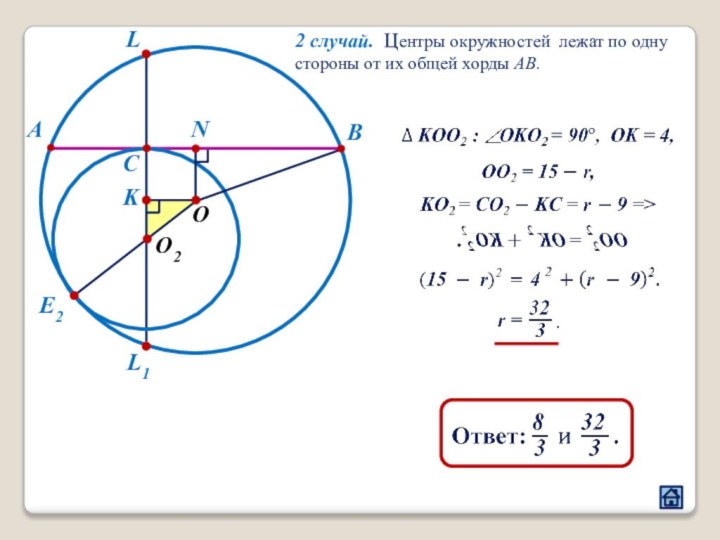
3.3 Расположение центров окружностей относительно общей хорды
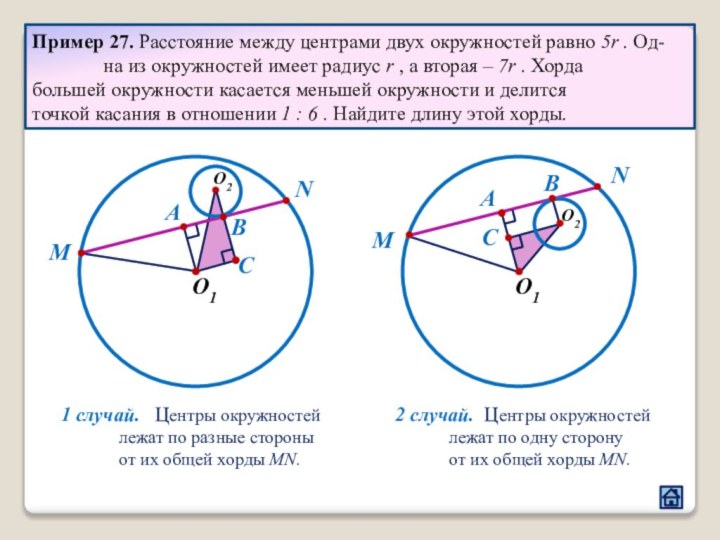
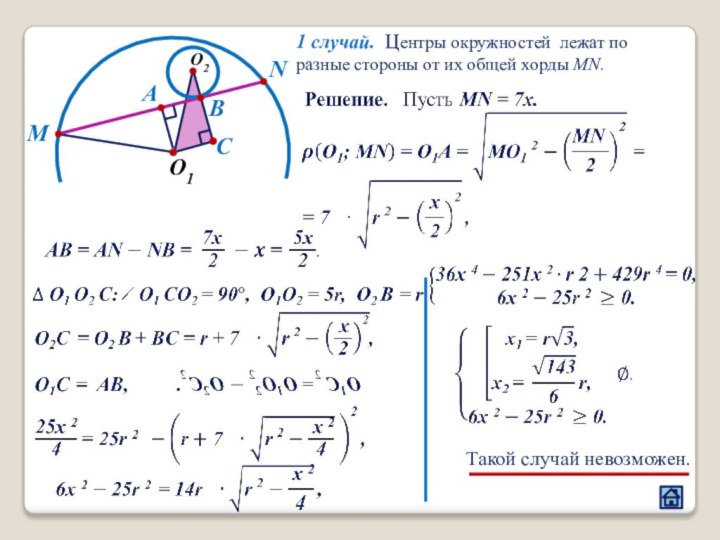
3.4 Расположение центров окружностей относительно хорды большей окружности
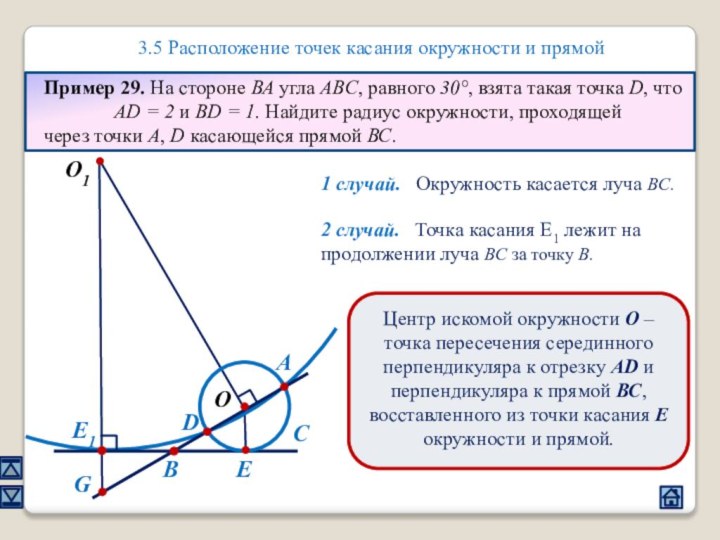
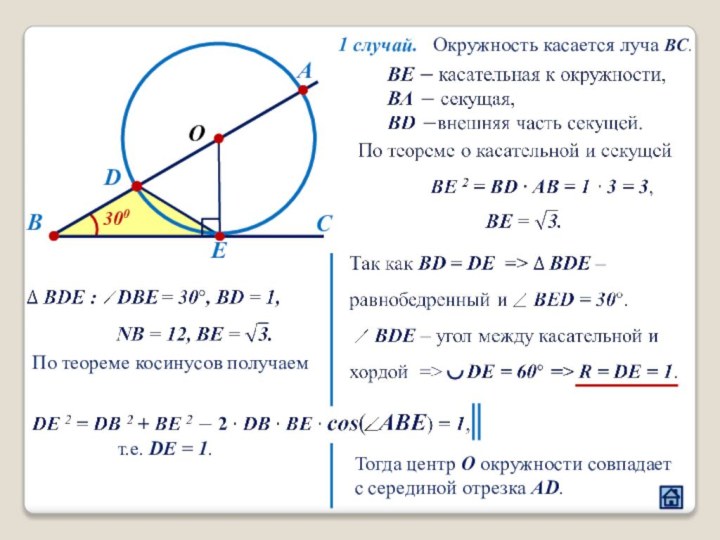
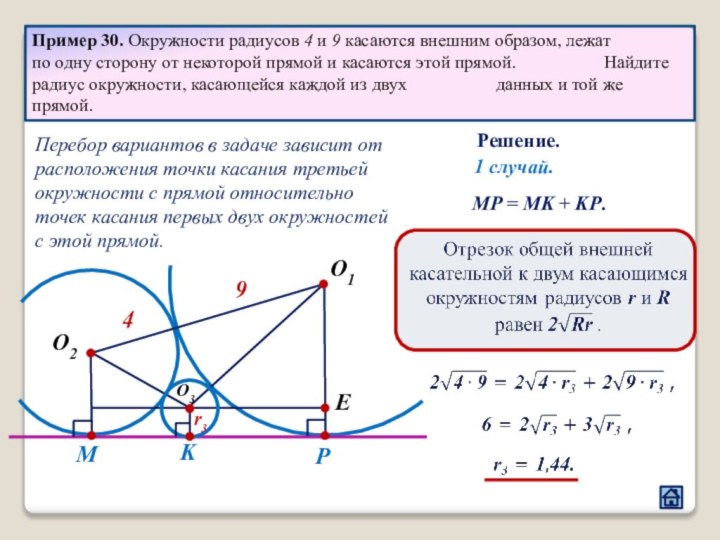
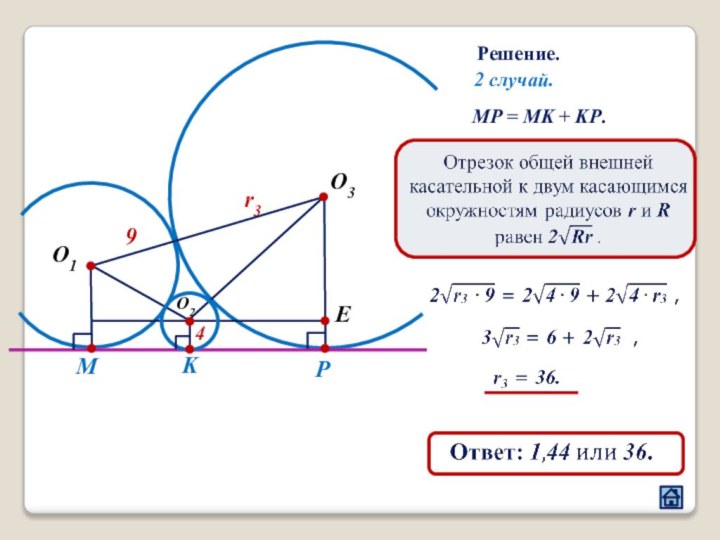
3.5 Расположение точек касания окружности и прямой
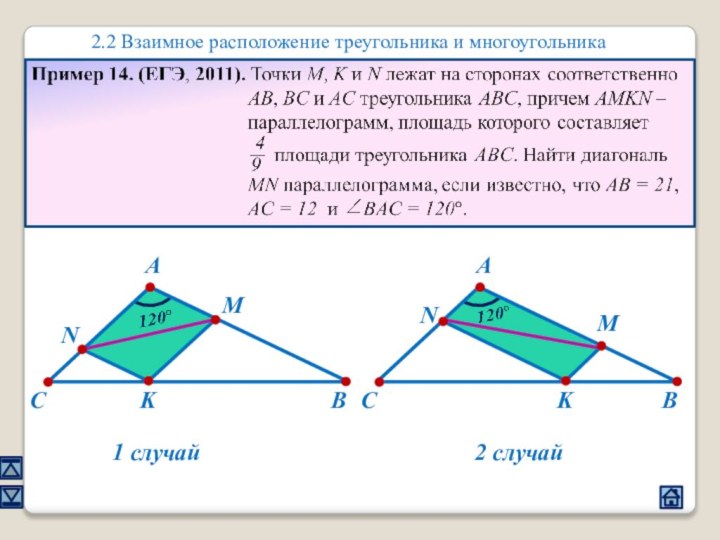
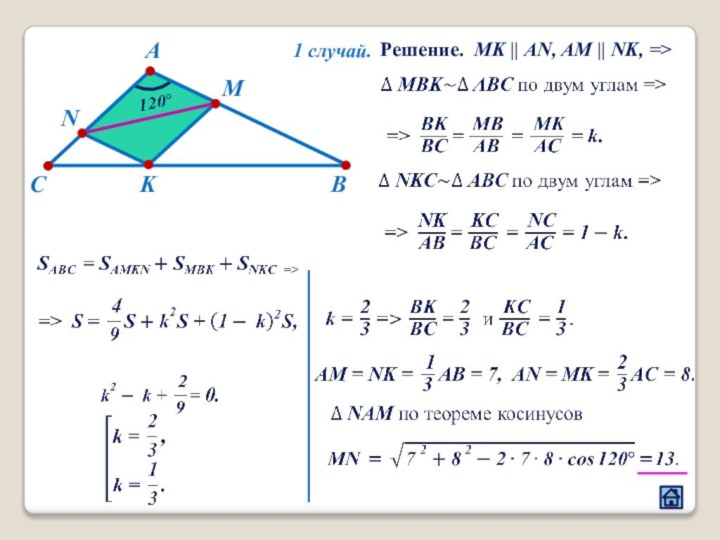
2.2 Взаимное расположение треугольника и многоугольника