Презентация на тему Решение простейших тригонометрических уравнений

Содержание

2. Под простейшими тригонометрическими уравнениями понимают уравнения вида:,где x – выражение с переменной, a∈.
3. xy10Масштаб π:3−1Рассмотрим решение уравнения sinx=a с помощью
4. xy10Масштаб π:3−1II случай: a∈[–1;1]Очевидно, что в
5. xy10Масштаб π:3−1aТаким образом, все корни в этом
6. xy10Масштаб π:3−1III случай: a= –1; 0
7. xy10Масштаб π:3−1Решение уравнения cosx=a рассмотрим тем же
8. xy10Масштаб π:3−1II случай: a∈[–1;1]Очевидно, что в
9. Таким образом, все корни в этом случае
10. III случай: a= –1; 0 или
11. 0y1x−1Решение уравнения tgx=a исследуйте самостоятельно:a
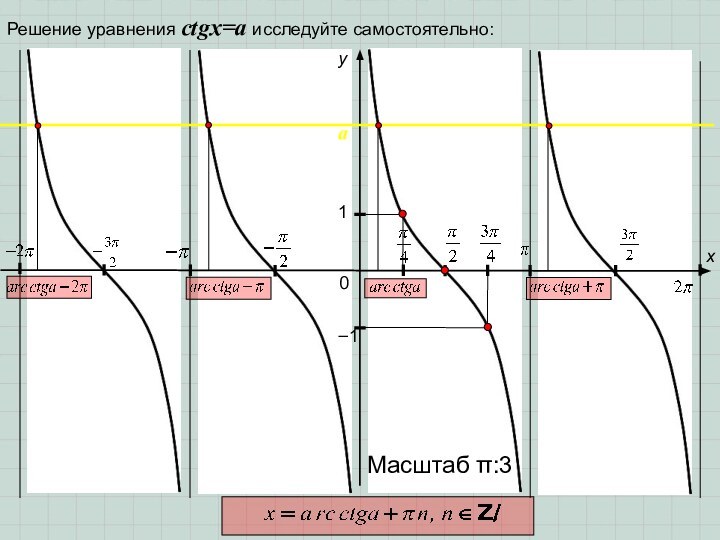
12. 0y1x−1Масштаб π:3Решение уравнения сtgx=a исследуйте самостоятельно:a
13. Скачать презентацию
14. Похожие презентации

Под простейшими тригонометрическими уравнениями понимают уравнения вида:,где x – выражение с переменной, a∈.

Главная
Алгебра
Решение простейших тригонометрических уравнений

Воробьев Леонид Альбертович, г.МинскАлгебра и начала анализа, 10 класс.Решение простейших тригонометрических уравнений.

Под простейшими тригонометрическими уравнениями понимают уравнения вида:,где x – выражение с переменной, a∈.

xy10Масштаб π:3−1Рассмотрим решение уравнения sinx=a с помощью графического способа решения. Для этого

xy10Масштаб π:3−1II случай: a∈[–1;1]Очевидно, что в этом случае точек пересечения бесконечно

xy10Масштаб π:3−1aТаким образом, все корни в этом случае можно записать в виде

xy10Масштаб π:3−1III случай: a= –1; 0 или 1.Эти три значения –

xy10Масштаб π:3−1Решение уравнения cosx=a рассмотрим тем же графическим способом. Для этого нам

Таким образом, все корни в этом случае можно записать в виде совокупности:Или,

III случай: a= –1; 0 или 1.Эти три значения – особые!

0y1x−1Решение уравнения tgx=a исследуйте самостоятельно:a

0y1x−1Масштаб π:3Решение уравнения сtgx=a исследуйте самостоятельно:a

Решение любых тригонометрических уравнений сводится к решению рассмотренных выше простейших тригонометрических уравнений.

Слайды презентации

Слайд 2 Под простейшими тригонометрическими уравнениями понимают уравнения вида:
,где x

– выражение с переменной, a∈.

Слайд 3 x
y
1
0
Масштаб π:3
−1
Рассмотрим решение уравнения sinx=a с помощью графического

xy10Масштаб π:3−1Рассмотрим решение уравнения sinx=a с помощью графического способа решения. Для

способа решения. Для этого нам надо найти абсциссы точек

пересечения синусоиды y=sinx и прямой y=a. Сразу же изобразим синусоиду.

I случай: a∉[–1;1]

Очевидно, что в этом случае точек пересечения нет и поэтому уравнение корней не имеет!

y=a, a>1

y=a, a<–1

Слайд 4 x
y
1
0
Масштаб π:3
−1
II случай: a∈[–1;1]
Очевидно, что в этом

случае точек пересечения бесконечно много, причем их абсциссы определяются

следующим образом:

1) Рассмотрим точку, абсцисса которой попадает на отрезок .

2) Абсцисса этой точки – есть число(угол в радианной мере), синус которого равен a, т.е. значение этого числа равно arcsina.

3) Абсцисса второй точки, попадающей на отрезок [–π; π], равна (π–arcsina). Для объяснения этого достаточно вспомнить, что sinx=sin(π–x).

4) Все остальные абсциссы точек пересечения получаются из этих двух добавлением к ним чисел вида 2πn, где n∈ (ведь мы помним свойство периодичности функции y=sinx). Задание: назовите, какие абсциссы «улетевших» за край чертежа двух точек?

Ответ: (arcsina+2π) и (3π – arcsina).