Слайд 2
Тематика заданий муниципального этапа олимпиады
VI-VII
Специальные олимпиадные
темы.
Числовые ребусы. Взвешивания.
Логические задачи. Истинные и ложные утверждения.
«Оценка +
пример».
Построение примеров и контрпримеров.
Инвариант.
Принцип Дирихле.
Разрезания.
Раскраски.
Игры.
Слайд 3
VIII-IХ КЛАССЫ
Специальные олимпиадные темы.
Логические задачи. Истинные и
ложные утверждения.
«Оценка + пример».
Построение примеров и
контрпримеров.
Принцип Дирихле.
Разрезания.
Раскраски.
Игры.
Инвариант.
Чётность.
Элементы комбинаторики.
Диофантовы уравнения (уравнения в целых числах).
Слайд 4
ЧЁТНОСТЬ
Теоретический материал
Известно, что целые числа бывают четными
и нечетными. Четные числа можно записать в виде 2k,
где k - целое число, а нечетные – в виде 2k +1 или 2k-1. Применение идеи четности и нечетности для решения олимпиадных задач основано на двух важных утверждениях:
Четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых.
Пример. Число 1+2+3+…+10 – нечетное, так как в сумме 5 нечетных слагаемых..
Число 3+5+7+9+11+13 – четное, так как в сумме 6 нечетных слагаемых.
Знак произведения нескольких (отличных от 0) чисел определяется четностью количества отрицательных сомножителей.
Слайд 5
Свойства четности:
1) Сумма четных чисел четна.
2)
Сумма двух нечетных чисел четна.
3) Сумма четного и
нечетного чисел нечетна.
4) Произведение любого числа на четное число четно.
5) Если произведение нечетно, то все сомножители нечетны.
6) Сумма нечетного количества нечетных чисел нечетна.
7) Сумма четного количества нечетных чисел четна.
8) Разность и сумма двух данных чисел есть числа одной четности.
9) Если объекты можно разбить на пары, то их количество четно.
Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.
Слайд 6
Пример 1. Могут ли 20 тетрадей ценой в
9, 11 и 13 рублей стоить в сумме 193
рубля?
Пример 2. Может ли сумма 1•2•3•…•М+1•2•3•…•К, где М, К принадлежит N и больше 3, оканчиваться на 9?
Пример 3. На столе лежат 6 монет, одна из них вверх орлом, другие – решкой. Можно ли все монеты положить вверх орлом, если можно одновременно переворачивать по две монеты?
Пример 4. 1. Кузнецу заказали выковать десять мечей. Каждый меч может стоить 3, 5 или 7 златников. Могут ли они стоить в сумме 53 златника?
Пример 5. На доске написаны числа 1, 2, 3, ..., 2005, 2006. Разрешается стереть с доски любые два числа и вместо них записать модуль их разности. В конце концов на доске останется одно число. Может ли оно равняться нулю?
Слайд 7
Теоретический материал
Принцип Дирихле – утверждение, сформулированное
немецким математиком Дирихле в 1834 году, устанавливающее связь между
объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий.
Принцип Дирихле выражает соотношение между двумя множествами. Самая популярная следующая формулировка принципа: «Если десять кроликов сидят в девяти ящиках, то в некотором ящике сидят не меньше двух кроликов».
Общая формулировка: Если n кроликов сидят в k ящиках, то найдётся ящик, в котором сидят не меньше чем n/k кроликов, и найдётся ящик, в котором сидят не больше чем n/k кроликов. Доказательство принципа Дирихле простое, но заслуживает внимания, поскольку похожие рассуждения часто встречаются.
Допустим, что в каждом ящике сидят меньше чем n/k кроликов. Тогда во всех ящиках вместе- кроликов меньше чем (n/k)•k=n. Противоречие.
Слайд 8
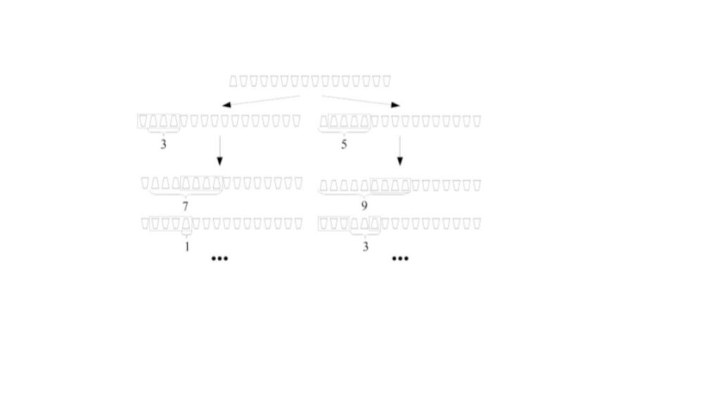
Пример 1. В магазин привезли 25 ящиков яблок
трех сортов, причем в каждом ящике лежат яблоки какого-то
одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
Пример 2. На олимпиаде 10 школьников решили в сумме 35 задач, причем среди них были решившие ровно одну, ровно две и ровно три задачи. Доказать, что кто-то из них решил не менее 5 задач.
Пример 3. В школе 400 учеников. Докажите, что хотя бы двое из них родились в один день года.
Пример 4. В классе учится 27 школьников, знающих (всего) 109 стихотворений. Докажите, что найдётся школьник, знающий не менее пяти стихотворений.
Пример 5. Докажите, что среди любых шести целых чисел найдутся два, разность которых кратна 5
Пример 6. 100 человек сидят за круглым столом, причем более половины из них — мужчины. Докажите, что какие-то двое мужчин сидят друг напротив друга.
Пример 7. Докажите, что среди степеней двойки есть две, разность которых делится на 2013.
Слайд 9
Перейдем теперь к обобщенному принципу Дирихле. На языке
кроликов и клеток его можно записать так:
если в 10
клетках сидит 51 кролик, то по крайней мере в одной клетке сидит не менее 6 кроликов.
ДОКАЗАТЕЛЬСТВО
Доказательство аналогично обычному принципу Дирихле. Действительно, если в каждой клетке сидит менее 6 кроликов, то во всех 10 клетках кроликов не более 50 — противоречие.
В математических терминах это выглядит так:
если элемент разбит на nk+1 множеств, то по крайней мере одно множество содержит не менее k+1 элементов.
Пример. Имеется 101 пуговица одного из 11 цветов. Докажите, что либо среди этих пуговиц найдутся 11 пуговиц одного цвета, либо 11 пуговиц разных цветов
Слайд 10
Оценка плюс пример
Оценка плюс пример — это метод
решения задач, который применяется при нахождении наибольших или наименьших
значений. Суть метода состоит в следующем. Предположим, что мы ищем наименьшее значение некоторой величины А .
Действуем в два этапа:
Оценка. Показываем, что выполнено неравенство А ≥. α
Пример. Предъявляем пример, когда достигается равенство .А = α
Тем самым доказываем, что наименьшее значение величины А равно .α
Слайд 11
Пример 1. Натуральные числа от 1 до 10
разбили на две группы так, что произведение чисел в
первой группе делится на произведение чисел во второй группе. Какое наименьшее значение может принимать частное от деления первого произведения на второе?
Пример 2. Каково наименьшее натуральное n такое, что n! делится на 18, на 19, на 20 и на 21?
Пример 3 Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 13 раз больше, либо в 13 раз меньше предыдущего. Сумма всех членов последовательности равна 6075. Какое наибольшее количество членов может быть в последовательности?
Слайд 12
ОПРЕДЕЛЕНИЕ
Инвариантом называется величина или некоторое свойство, которое не меняется
при заданных преобразованиях.
Инвариант
Инвариант — термин, используемый в математике и
физике, а также в программировании, обозначает нечто неизменяемое. Все задачи, объединённые условным названием «инвариант», имеют следующий вид: даны некоторые объекты, над которыми разрешается выполнять определённые операции. Как правило, в задаче спрашивается, можно ли при помощи этих операций из одного объекта получить другой? Если можно, то нужно привести пример, как это сделать. Если нельзя, нужно доказать, что это невозможно.
В качестве инварианта могут выступать самые разные величины: чётность, сумма, произведение, остаток по некоторому модулю и т.д.
Слайд 13
Пример1. На столе стоят 16 стаканов. При
этом 15 стаканов стоят правильно, а один перевёрнут донышком
вверх. Разрешается одновременно переворачивать любые 4 стакана. Можно ли при помощи таких операций добиться того, чтобы все стаканы стояли правильно?
Слайд 15
Пример. 100 фишек выставлены в ряд. Разрешено менять
местами две фишки, стоящие через одну фишку. Можно ли
с помощью таких операций переставить все фишки в обратном порядке?
Слайд 16
Пример3. На шести ёлках сидят шесть чижей, на
каждой ёлке — по чижу. Ёлки растут в ряд
с интервалами 10 метров. Если какой-то чиж перелетает с одной ёлки на другую, то какой-то другой чиж обязательно перелетает на столько же метров, только в обратном направлении. Могут ли все чижи собраться на одной ёлке? А если чижей и ёлок – семь?
Слайд 17
Какова общая стратегия решения задач на инварианты?
Во-первых,

инвариант нужно заметить.
Для этого можно смоделировать разные последовательности
применения операций и выделить какое-то характерное условие, которое всегда выполняется.
Во-вторых, нужно доказать, что инвариант будет выполняться при любом применении операций. В разобранных задачах это довольно очевидно. Строго говоря, для доказательства используется метод математической индукции.
Пусть нужно доказать, что некоторый инвариант будет выполняться после любого числа допустимых операций. Обозначим число операций через n и начнём доказательство по индукции. Сначала нужно доказать базу индукции — инвариант выполняется в самом начале, т.е. при n = 0.
Затем доказывается переход индукции: показывается, что из выполнения инварианта после n операций следует его выполнение после n + 1 операции, т.е. что допустимые операции не влияют на инвариант. По индукции отсюда следует, что инвариант будет выполняться после любых n операций для любого целого n > 0.
Слайд 18
Пример 4.
На столе лежит куча из n ракушек.
Из нее убирают одну ракушку и кучу делят на
две (не обязательно поровну). Затем из какойнибудь кучи, содержащей более одной ракушки, снова убирают одну ракушку и снова кучу делят на две. И так далее. Можно ли через несколько ходов оставить на столе только кучи, состоящие из трёх ракушек при n = 635 и n = 637?