Слайд 3
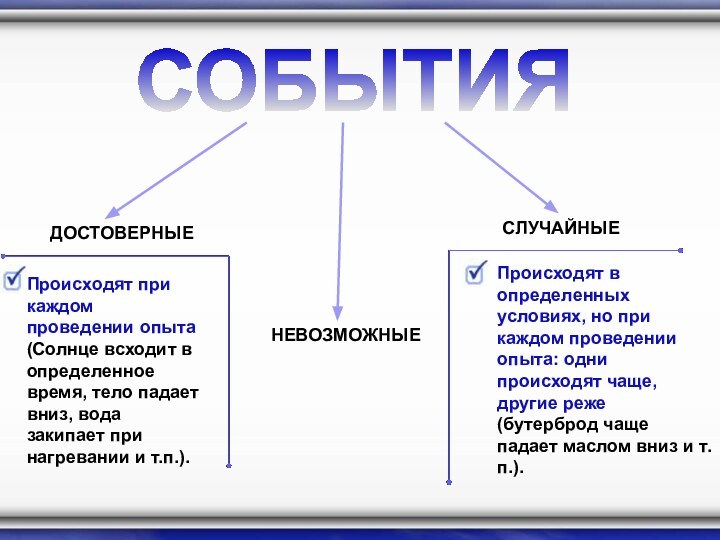
СОБЫТИЯ
ДОСТОВЕРНЫЕ
СЛУЧАЙНЫЕ
Происходят при каждом проведении опыта (Солнце всходит в
определенное время, тело падает вниз, вода закипает при нагревании
и т.п.).
Происходят в определенных условиях, но при каждом проведении опыта: одни происходят чаще, другие реже (бутерброд чаще падает маслом вниз и т.п.).
НЕВОЗМОЖНЫЕ
Слайд 4
ТЕСТ
«Случайные исходы, события, испытания».
Слайд 5
1. О каком событии идёт речь? «Из 25
учащихся класса двое справляют
день рождения 30 февраля».
А) достоверное;
В) невозможное; С) случайное
2. Это событие является
случайным:
А) слово начинается с буквы«ь»;
В) ученику 9 класса 14 месяцев;
С) бросили две игральные
кости: сумма выпавших на
них очков равна 8.
Найдите достоверное
событие:
А) На уроке математики ученики
делали физические упражнения;
В) Сборная России по футболу не
станет чемпионом мира 2005 года;
С) Подкинули монету и она упала
на «Орла».
Слайд 8
4. Среди пар событий, найдите
несовместимые.
А) В сыгранной Катей и Славой
партии шахмат,
Катя проиграла и
Слава проиграл.
В) Из набора домино вынута одна
костяшка, на ней одно число очков больше 3, другое число 5.
С) Наступило лето, на небе ни облачка.
Слайд 9
5.Охарактеризуйте случайное
событие:
«новая электролампа не загорится».
Это событие:
А) менее вероятно ;
В) равновероятное ;
С) более вероятное.
Слайд 10
6. Какие события
из
перечисленных ниже являются
противоположными? В колоде карт
лежат четыре туза и четыре короля
разных мастей. Достают карту наугад. Событие:
А) достанут трефового туза;
В) достанут туза любой масти;
С) достанут любую карту кроме
трефового туза.
Слайд 11
7. Колобок катится по лесным тропкам
куда глаза глядят.
На полянке его
тропинка расходится на четыре тропинки,
в
конце которых Колобка поджидают
Заяц, Волк, Медведь и Лиса. Сколько
исходов для выбора Колобком наугад
одной из четырёх тропинок.
А) 1; В) 4; С) 5.
Слайд 12
8. Два стрелка делают по одному
выстрелу в
мишень. Сколько
исходов двух совместных
выстрелов?
А) 4;
В) 3; С) 2.
Слайд 13
9. Два шахматиста играют подряд
две партии. Сколько
исходов у
этого события?
А) 4;
В) 2; С) 9.
Слайд 14
10*. Случайный опыт состоит в
выяснении пола детей в
семьях с
тремя детьми. Сколько возможных
исходов у этого опыта?
А) 8; В) 9; С) 6.
Слайд 16
В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность
– возможность исполнения, осуществимости чего-нибудь».
Основатель современной теории вероятностей А.Н.Колмогоров:
«Вероятность
математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
Слайд 17
Известно, по крайней мере, шесть основных
схем определения и понимания вероятности. Не все они в
равной мере используются на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование.
Понятие вероятности
Слайд 18
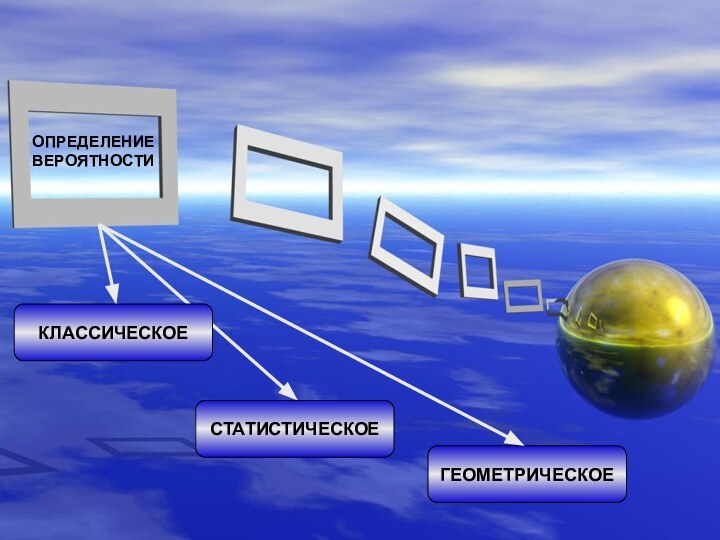
КЛАССИЧЕСКОЕ
СТАТИСТИЧЕСКОЕ
ГЕОМЕТРИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Слайд 19
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Слайд 20
ВЕРОЯТНОСТЬ
– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО
СОБЫТИЯ.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ
ВЕРОЯТНОСТИ СОБЫТИЯ:
А – некоторое событие,
m – количество исходов, при которых событие А появляется,
n – конечное число равновозможных исходов.
P – обозначение происходит от первой буквы французского слова probabilite – вероятность.
Слайд 21
Вероятностью Р наступления случайного события А
называется отношение , где n – число всех
возможных исходов эксперимента, а m – число всех благоприятных исходов:
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Слайд 22
Пьер-Симо́н Лапла́с
Классическое определение вероятности было впервые дано
в работах французского математика Лапласа.
Слайд 23
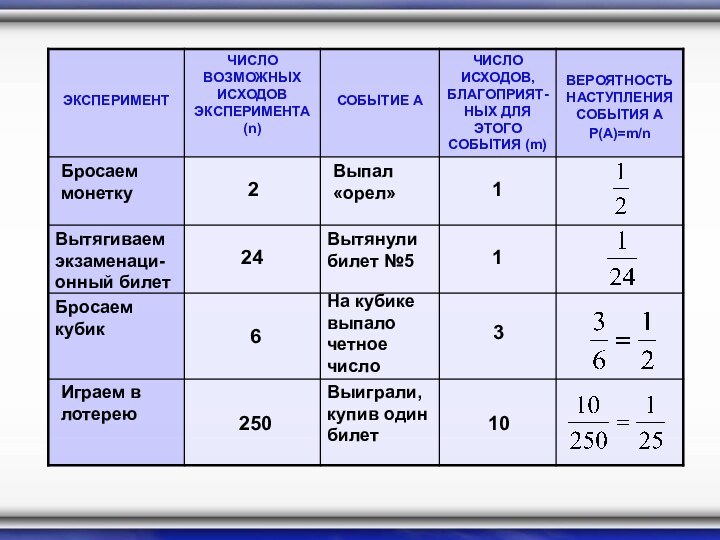
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем
кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один
билет
250
10
Слайд 24
Пример 1
В школе 1300 человек, из
них
5 человек хулиганы.
Какова вероятность того, что один из них попадётся директору на глаза?
Слайд 25
Вероятность:
P(A) = 5/1300 = 1/250.
Решение
Слайд 26
Пример 2.
При игре в нарды бросают 2
игральных кубика. Какова вероятность того, что на обоих кубиках
выпадут одинаковые числа?
Слайд 27
Решение
Составим следующую таблицу
Вероятность: P(A)=6/36= =1/6.
Слайд 28
Пример 3.
Из карточек составили слово «статистика». Какую карточку
с буквой вероятнее всего вытащить? Какие события равновероятные?
с
т
а
т
и
с
т
и
к
а
Слайд 29
Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10 = 1/5;
буква «т» встречается 3 раза
–
P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение
Слайд 31
Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А не меньше , но не
больше
?
1
?
?
?
0
1
0
Слайд 32
P(u) = 1 (u – достоверное событие);
P(v) =
0 (v – невозможное событие);
0 P(A) 1.
Слайд 34
Задача 1.
В коробке 4 синих, 3 белых
и 2 желтых фишки. Они тщательно перемешиваются, и наудачу
извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.
Слайд 35
а) Мы имеем всевозможных случаев 9. Благоприятствующих событий
3. Вероятность равна:
P=3:9=1/3=0,33(3)
б) Мы имеем всевозможных случаев 9. Благоприятствующих
событий 2. Вероятность равна P=2:9=0,2(2)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
Решение
Слайд 36
Задача 2.
В коробке лежат 10 одинаковых шаров,
на каждом из которых написан его номер от 1
до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.
Слайд 37
Всевозможных событий 6 (красный №1 - красный №2;
красный №1 - белый; красный №2 - белый; красный
№3 - красный №2; красный №3 - красный №1; красный №3 - белый) из них благоприятных 3. Выигрывает тот, кто вытаскивает 2 красных шара.
Решение
Слайд 38
Задача 3.
Мальчики играли в “Орлянку”. Но монетка
куда-то закатилась. Предложите, как заменить ее игральным кубиком?
Слайд 39
Считать "орел" - четное число, а "решка" -
не четное число.
Решение
Слайд 40
Задача 4.
Какую справедливую игру можно предложить двум
девочкам, у которых есть 3 красных и 1 белый
шарик и мешок?
Слайд 41
Всевозможных событий 6 (красный №1 - красный №2;
красный №1 - белый; красный №2 - белый; красный
№3 - красный №2; красный №3 - красный №1; красный №3 - белый) из них благоприятных 3. Выигрывает тот, кто вытаскивает 2 красных шара.
Решение
Слайд 42
Задача 5.
В настольной игре сломалась вертушка с
тремя разными секторами: красным, белым и синим, но есть
кубик. Как заменить вертушку?
Слайд 43
Считать на кубике 1 и 2 - красный
сектор, 3 и 4 - синий сектор, 5 и
6 - белый сектор.
Решение