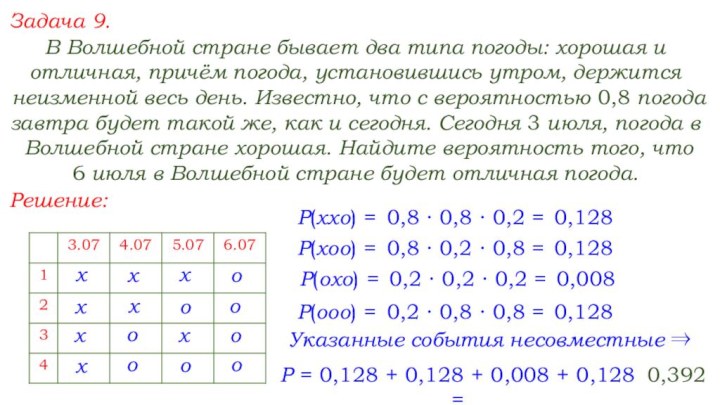
окончится случайный опыт.
Сумма вероятностей всех элементарных событий равна 1.
Р(А)
равна сумме вероятностей элементарных событий, благоприятствующих этому событию.А ⋃ В (объединение) – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий А,В
А ⋂ В (пересечение) – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.
Ā называется противоположным событию А, если состоит из тех и только тех элементарных исходов, которые не входят в А.
Несовместные события – это события, которые не наступают в одном опыте.