Что такое findtheslide.com?

FindTheSlide.com - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Прямоугольный параллелепипед

Содержание

ПараллелепипедПараллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8 вершин и 12 рёбер. Грани параллелепипеда, не имеющие общих вершин, называются
Прямоугольный параллелепипед.Работу выполнилаУченица 5 «В» классаМендыгалиева АлинаМОУ «Гимназия» №6 ПараллелепипедПараллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8 ВершиныРёбраДлинаШиринаВысота ПараллелепипедОни равны и лежат в параллельных плоскостях. ПараллелепипедПараллелепипед называется прямым или прямоугольным, если все его грани – прямоугольники; это ПараллелепипедДлины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называются его измерениями. Квадрат ПараллелепипедОбъём параллелепипеда равен произведению площади основания (какой – либо его грани) на ПараллелепипедНазвание «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого слова Объём прямоугольного параллелепипеда.Найди объём V1 прямоугольного параллелепипеда с размерами a, b и Представь положение жирной линии в пространстве и согни её из проволоки. 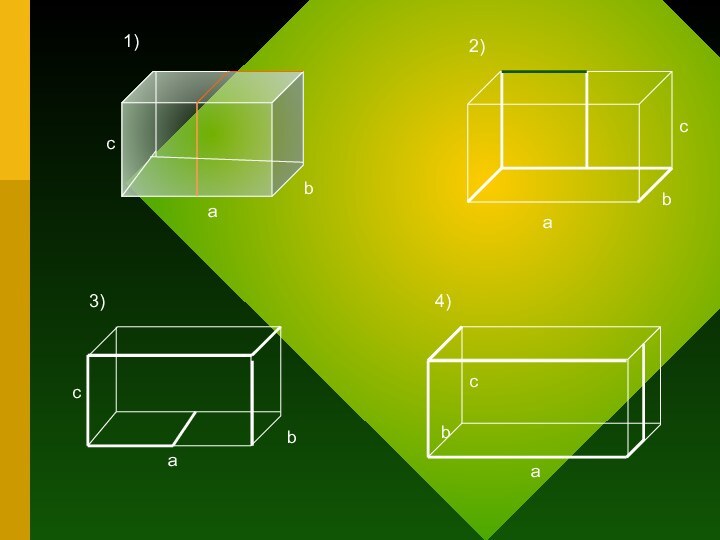1)саb2)bас3)аbсbас4) Спасибо за внимание!
Слайды презентации

Слайд 1 Прямоугольный параллелепипед.
Работу выполнила
Ученица 5 «В» класса
Мендыгалиева Алина
МОУ «Гимназия» №6

Прямоугольный параллелепипед.Работу выполнилаУченица 5 «В» классаМендыгалиева АлинаМОУ «Гимназия» №6

Слайд 2 Параллелепипед
Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед

имеет 8 вершин и 12 рёбер. Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
ПараллелепипедПараллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет

Слайд 3
Вершины
Рёбра
Длина
Ширина
Высота

ВершиныРёбраДлинаШиринаВысота

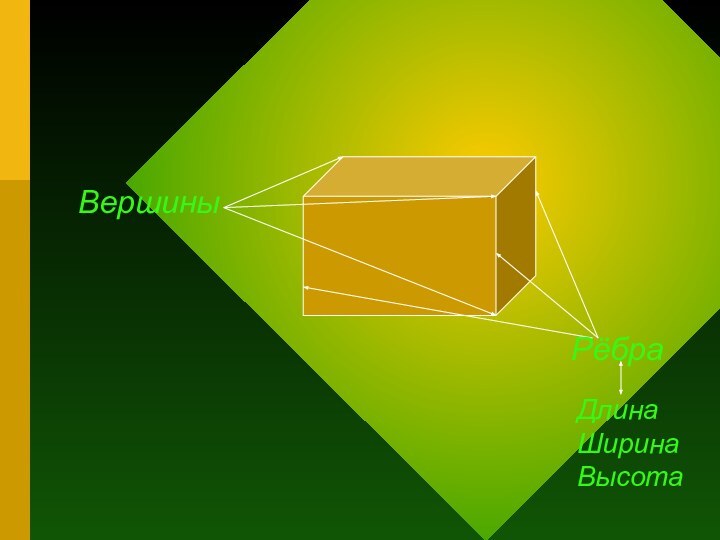
Слайд 4 Параллелепипед
Они равны и лежат в параллельных плоскостях.

Диагонали параллелепипеда, то есть отрезки, соединяющие вершины параллелепипеда, не принадлежащие какой – либо одной грани, пересекаются в одной точке и делятся ею по полам.


ПараллелепипедОни равны и лежат в параллельных плоскостях.

Слайд 5 Параллелепипед
Параллелепипед называется прямым или прямоугольным, если все его грани –

прямоугольники; это - прямая четырёхугольная призма. Параллелепипед, все грани которого квадраты, называется кубом.


ПараллелепипедПараллелепипед называется прямым или прямоугольным, если все его грани – прямоугольники;

Слайд 6 Параллелепипед
Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называются его

измерениями. Квадрат длинны диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.


ПараллелепипедДлины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называются его измерениями.

Слайд 7 Параллелепипед
Объём параллелепипеда равен произведению площади основания (какой – либо его

грани) на высоту (расстояние между основанием и противоположной гранью). Объём прямоугольного параллелепипеда равен произведению трёх его измерений.


ПараллелепипедОбъём параллелепипеда равен произведению площади основания (какой – либо его грани)

Слайд 8 Параллелепипед
Название «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и

греческого слова «эпипедос», означающего «плоскость», «поверхность». Слово встречалось у древнегреческих ученых Евклида и Герона.


ПараллелепипедНазвание «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого

Слайд 9 Объём прямоугольного параллелепипеда.
Найди объём V1 прямоугольного параллелепипеда с размерами a,

b и c, сумму Р длин всех его рёбер и длину l жирной линии, у которой концы и точки перегиба – вершины параллелепипеда или середины его рёбер. Найди объём V2 параллелепипеда с размерами в два раза меньше.
Объём прямоугольного параллелепипеда.Найди объём V1 прямоугольного параллелепипеда с размерами a, b

Слайд 10
Представь положение жирной линии в пространстве и согни её из

проволоки.
Представь положение жирной линии в пространстве и согни её из проволоки.

Слайд 11 1)

с
а
b
2)

b
а
с
3)

а
b
с

b
а
с
4)

1)саb2)bас3)аbсbас4)

Слайд 12

Слайд 13 Спасибо за внимание!

Спасибо за внимание!
  • Имя файла: pryamougolnyy-parallelepiped.pptx
  • Количество просмотров: 74
  • Количество скачиваний: 0

Похожие презентации

Геометрия Лобачевского Геометрия Лобачевского 86
Презентация по геометрии на тему Треугольники Презентация по геометрии на тему Треугольники 87
Конус. Сечение конуса плоскостями Конус. Сечение конуса плоскостями 84
Правильные многоугольники Правильные многоугольники 82
Геометрия четырехугольник Геометрия четырехугольник 74
Презентация по математике Теорема Пифагора (8 класс) Презентация по математике Теорема Пифагора (8 класс) 72
Презентация к уроку геометрии в 11 классе Понятие цилиндра Презентация к уроку геометрии в 11 классе Понятие цилиндра 85
Презентация по геометрии на темуСамостоятельная работа по темеСвойства параллельных прямых(7 класс) Презентация по геометрии на темуСамостоятельная работа по темеСвойства параллельных прямых(7 класс) 81
Использование графовых моделей при решении задач Использование графовых моделей при решении задач 57
Виды углов Виды углов 69
Параллельность прямых Параллельность прямых 70
Презентация по геометрии на тему: Соотношения между сторонами и углами в прямоугольном треугольнике(8 класс) Презентация по геометрии на тему: Соотношения между сторонами и углами в прямоугольном треугольнике(8 класс) 79
Геометрияда тапсырмаларды орындау 7 сынып Геометрияда тапсырмаларды орындау 7 сынып 105
Презентация по математике на тему Теорема Пифагора(8 класс) Презентация по математике на тему Теорема Пифагора(8 класс) 70
Программа авторского элективного курса интегрированного содержания по математике Красота и музыка правильных многогранников для учащихся 10-11 общеобразовательных классов Программа авторского элективного курса интегрированного содержания по математике Красота и музыка правильных многогранников для учащихся 10-11 общеобразовательных классов 64
Расстояние от точки до прямой Расстояние от точки до прямой 72
Шар 11 класс Шар 11 класс 68
Применение двумерных диаграмм Применение двумерных диаграмм 86
Презентация к проекту: Симметрия в пространстве Презентация к проекту: Симметрия в пространстве 91
Радианная мера угла Радианная мера угла 98
Арифметические действия над положительными и отрицательными числами. Лекарственные растения наслега КЮСЮР. Арифметические действия над положительными и отрицательными числами. Лекарственные растения наслега КЮСЮР. 60
Геометрические задачи на построение Геометрические задачи на построение 85
Перпендикулярность в пространстве геометрия Перпендикулярность в пространстве геометрия 65
Площадь криволинейной трапеции Площадь криволинейной трапеции 73
Презентация по математике на тему Построение фигур одним росчерком пера. Презентация по математике на тему Построение фигур одним росчерком пера. 126
Развитие геометрии Развитие геометрии 85
Элементы правильных многогранников Элементы правильных многогранников 53
Разнообразный мир линий Разнообразный мир линий 91
Презентация История развития геометрии Презентация История развития геометрии 78
Презентация Применение аксиом стереометрии Презентация Применение аксиом стереометрии 104