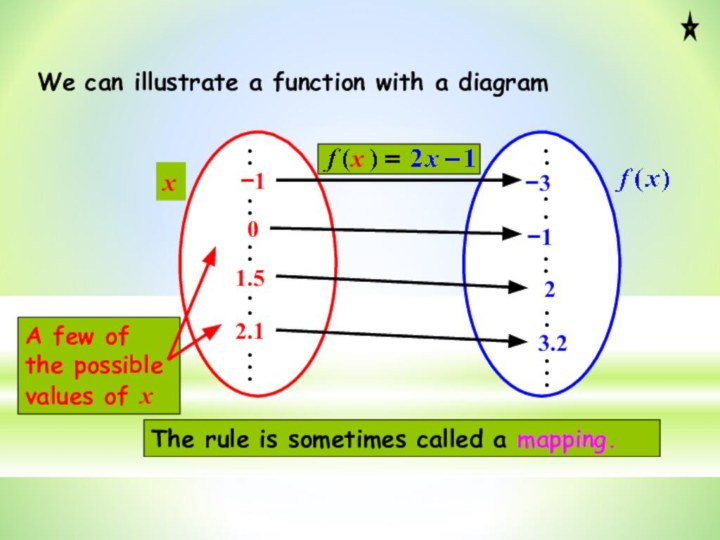
can illustrate a function with a diagram
The rule
is sometimes called a mapping.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



























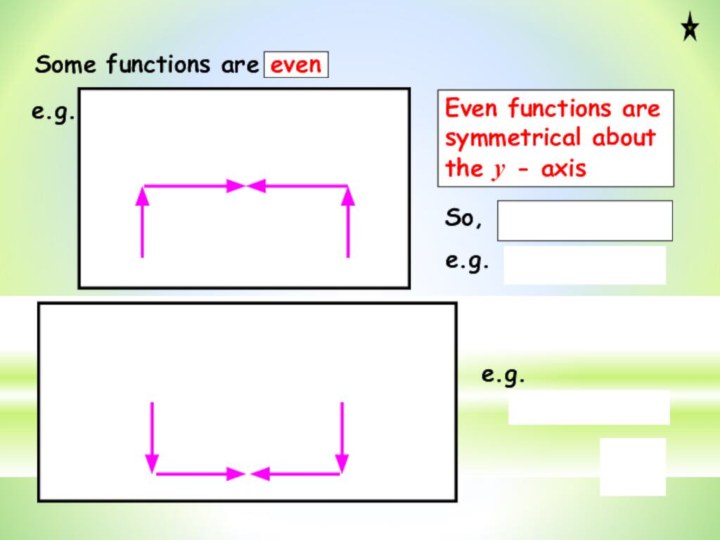
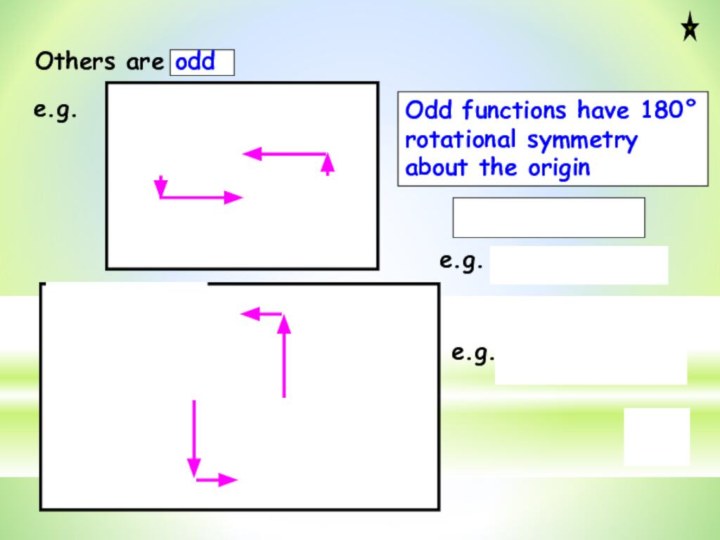


A bit more jargon
To define a function fully, we need to know the values of x that can be used.
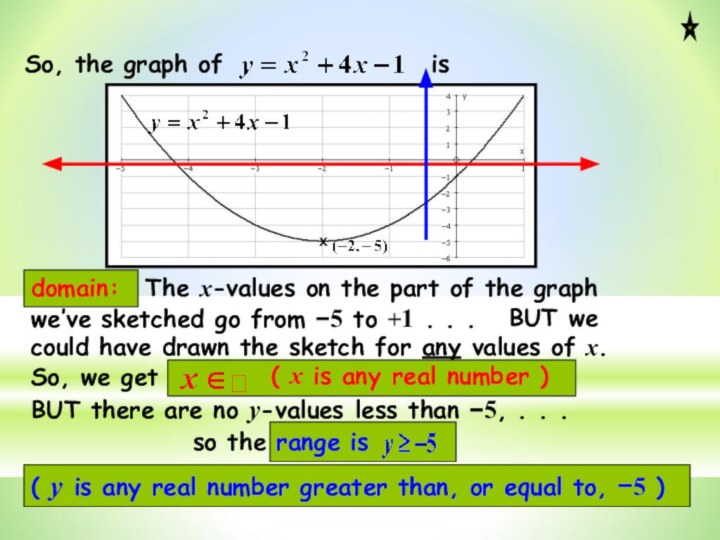
BUT we could have drawn the sketch for any values of x.
( y is any real number greater than, or equal to, −5 )
BUT there are no y-values less than −5, . . .
domain:
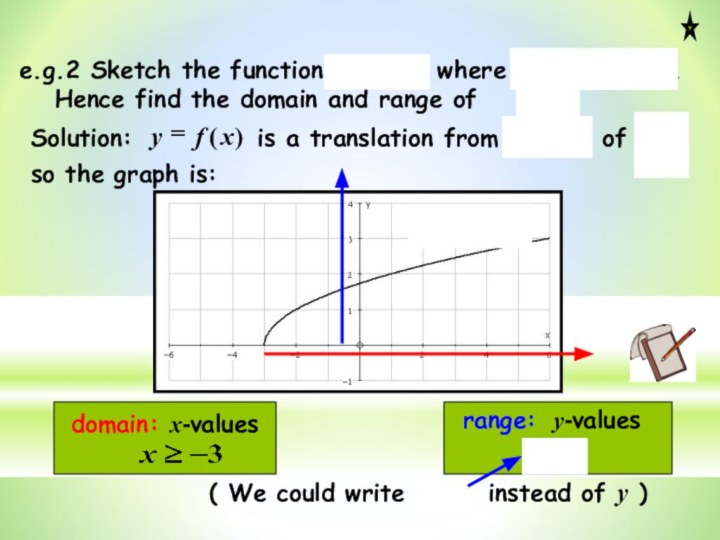
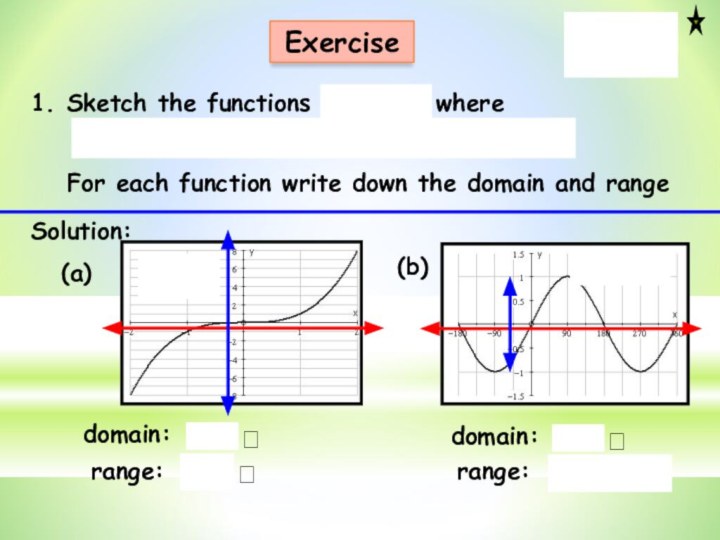
Solution:
Other values are greater than zero.
So, the range is