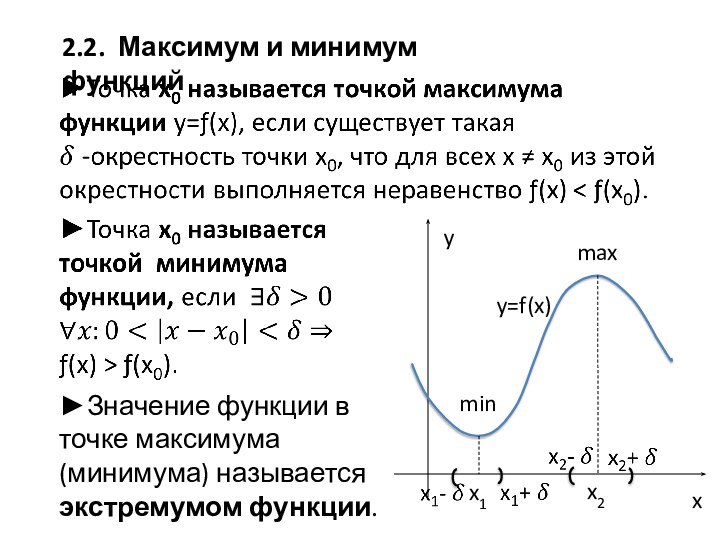
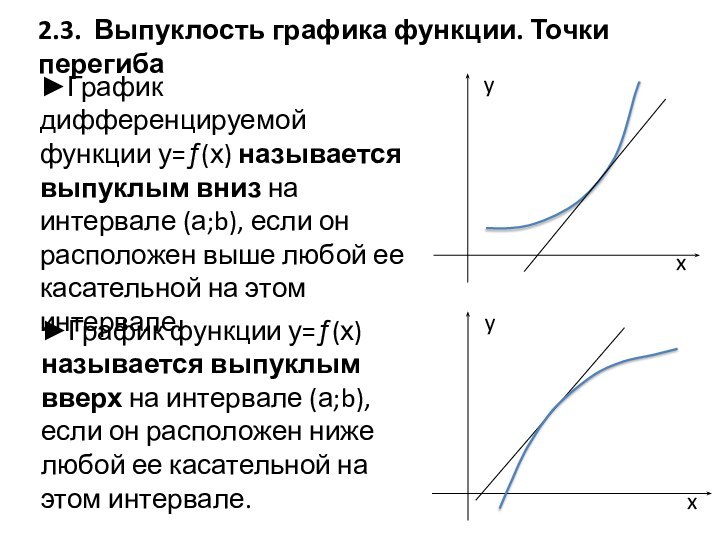
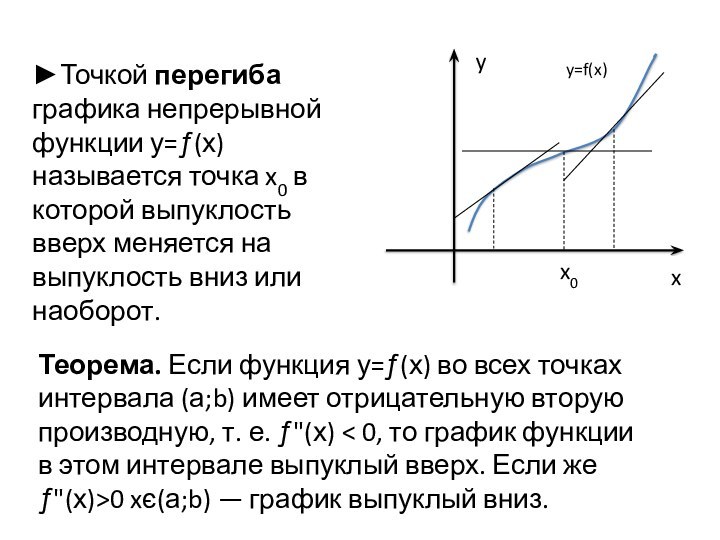
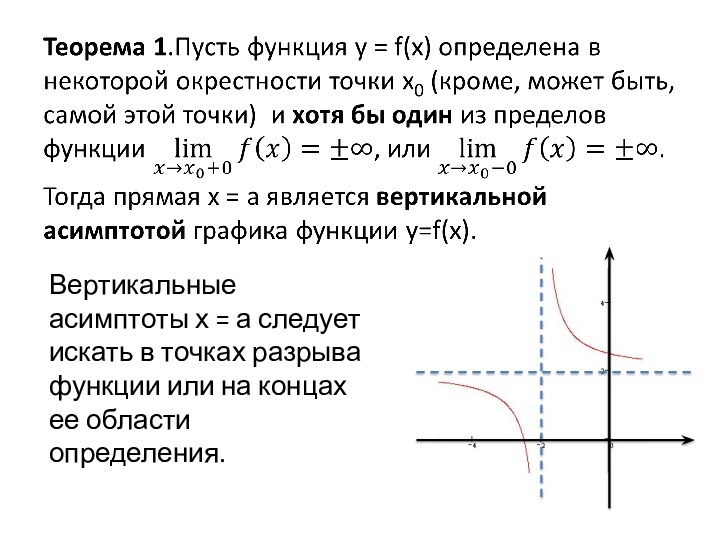
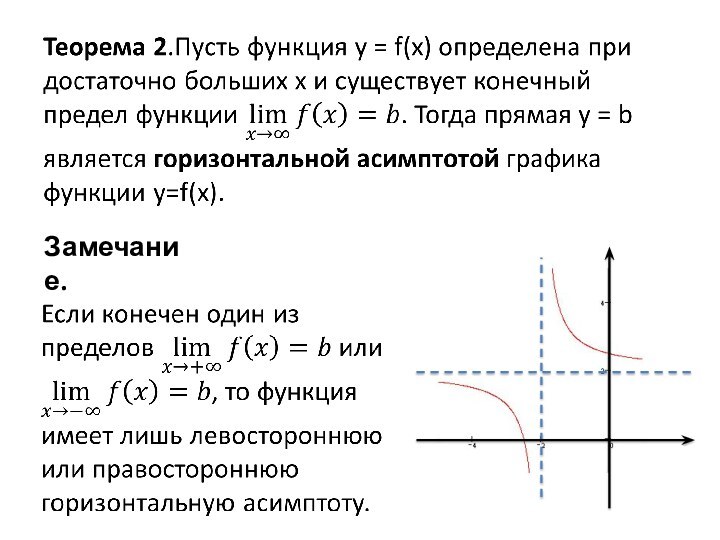
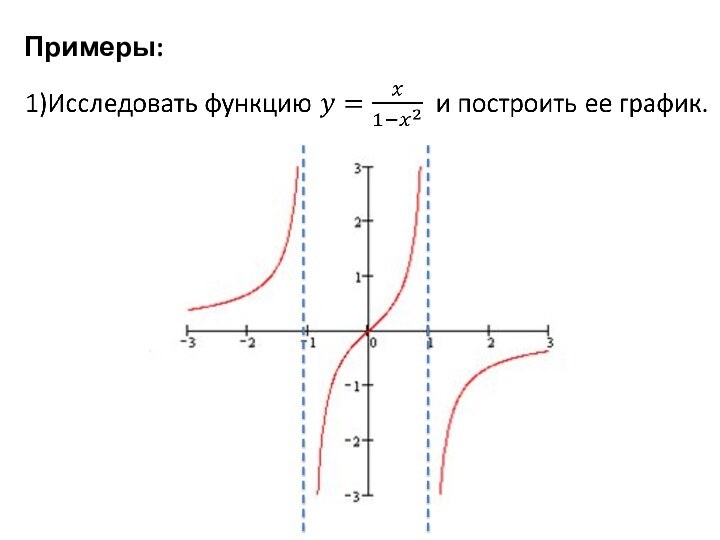
убывание функций
Теорема (необходимые условия возрастания и убывания функции).
Если дифференцируемая
на интервале (a;b) функция ƒ(х) возрастает (убывает), то ƒ'(х) ≥ 0 (ƒ'(х)≤0) для x є (a;b).Геометрически теорема означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ох или в некоторых точках параллельны оси Ох.