функция
способы задания функции
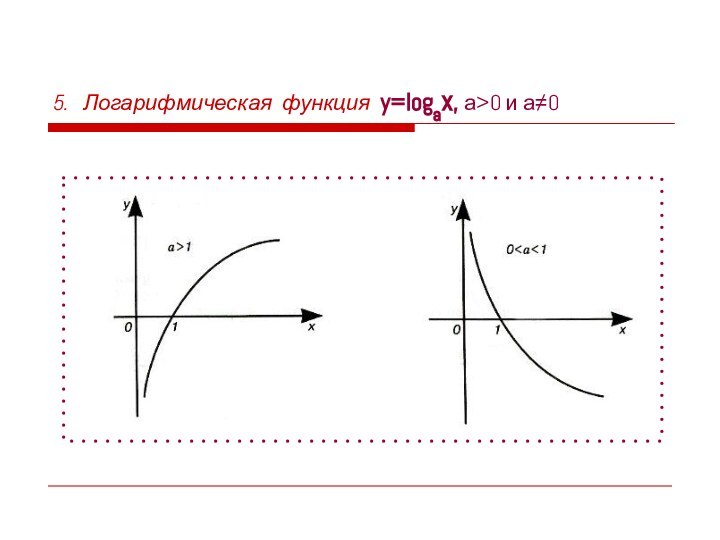
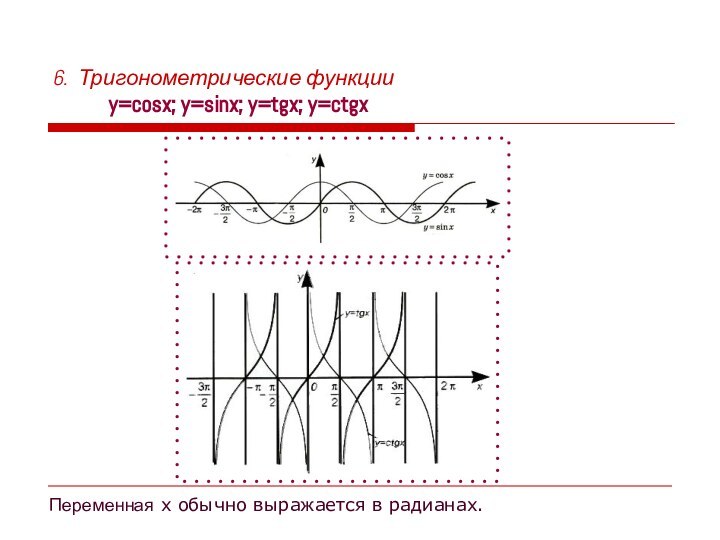
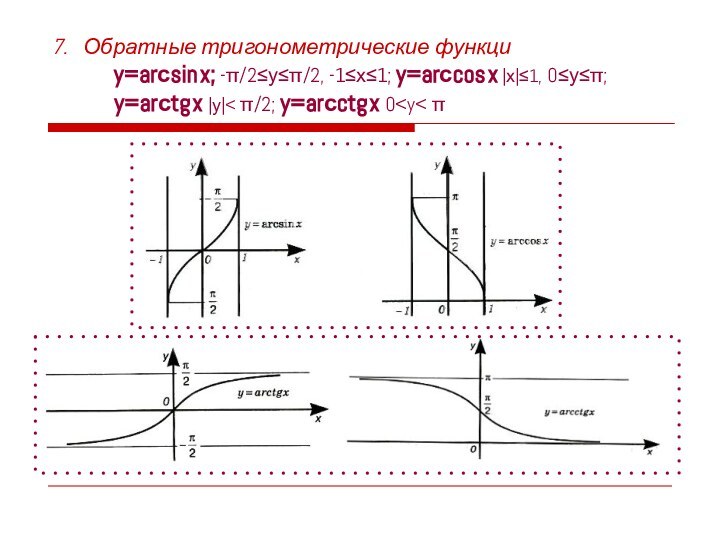
Основные элементарные функции, их свойства, графики
Непрерывность функции.
Предел функцииБесконечно малые и бесконечно большие величины
Основные теоремы о пределах
Методы раскрытия неопределенностей