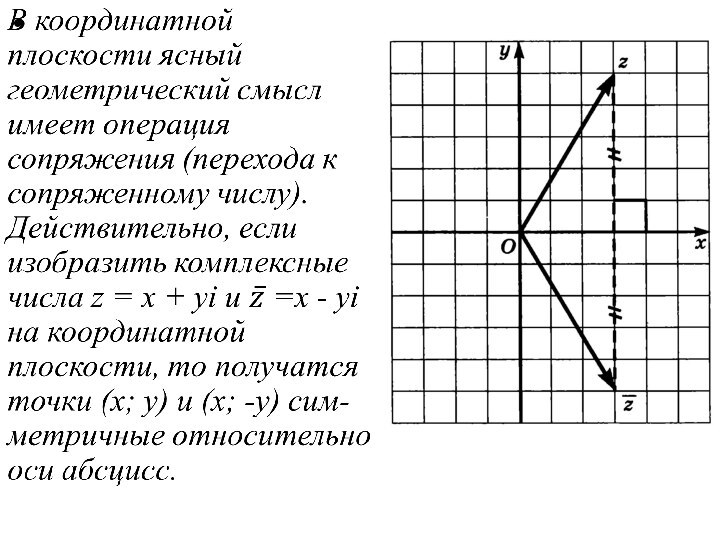
Слайд 2
Геометрической моделью множества С является координатная плоскость. Каждому
комплексному числу r = а + bi можно естественным
образом поставить в соответствие точку (а; b) координатной плоскости.
Тогда любому комплексному числу соответствует единственная точка на координатной плоскости, и наоборот, каждая точка плоскости является «изображением» единственного комплексного числа.
Слайд 4
При таком соответствии действительному числу а = а
+ 0 • i соответствует точка (а; 0) с
нулевой ординатой. Значит, действительные числа изображаются точками оси абсцисс.
Мнимой единице i = 0 + 1 • i соответствует точка (0; 1) на оси ординат, и вообще точками этой оси будут изображаться все чисто мнимые числа.
Слайд 5
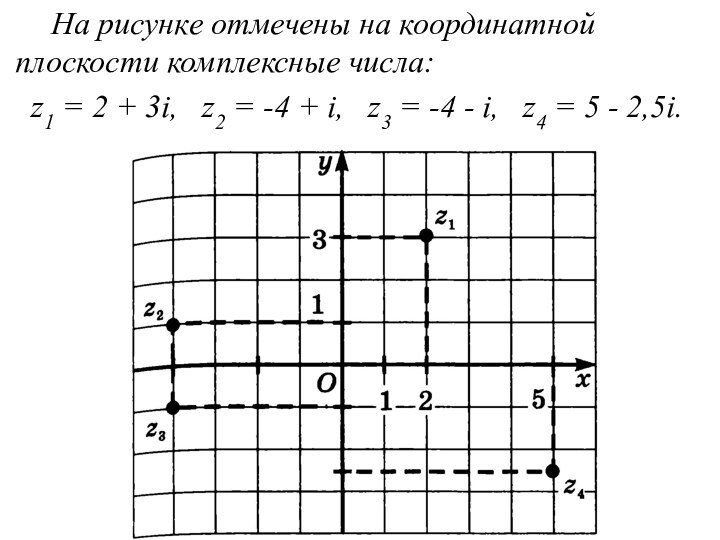
На рисунке отмечены на координатной плоскости комплексные числа:
z1 = 2 + 3i, z2 = -4
+ i, z3 = -4 - i, z4 = 5 - 2,5i.
Слайд 6
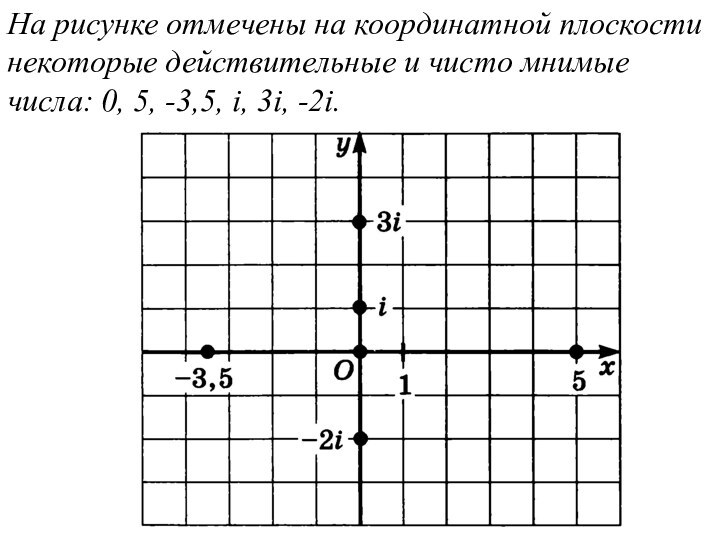
На рисунке отмечены на координатной плоскости некоторые действительные
и чисто мнимые числа: 0, 5, -3,5, i, 3i,
-2i.
Слайд 8
То есть, для таким образом определенных суммы и
произведения комплексных чисел верны сочетательный, переместительный и распределительный законы.
При этом пара (0; 0) будет нулем относительно сложения, а пара (1; 0) будет единицей относительно умножения комплексных чисел.
Слайд 9
Пример 1. Изобразить на координатной плоскости множество всех
комплексных чисел, у которых:
а) действительная часть равна -4;
б) мнимая часть является
четным однозначным натуральным числом;
в) отношение мнимой части к действительной равно 2;
г) сумма квадратов действительной и мнимой частей равна 9.
Слайд 10
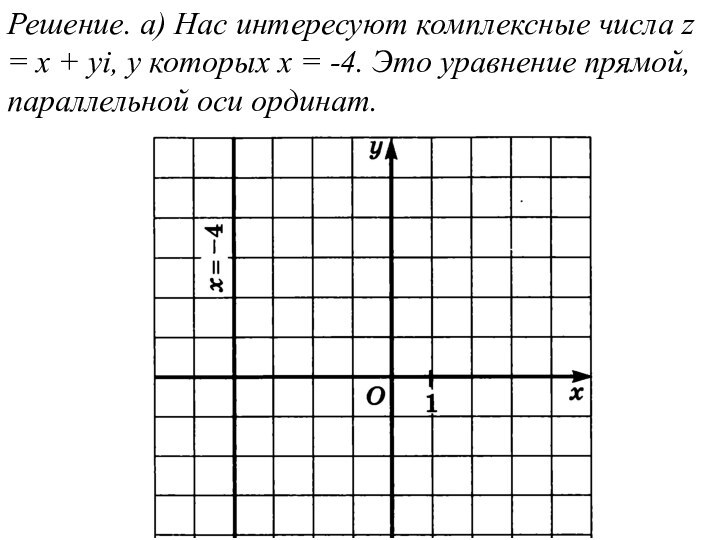
Решение. а) Нас интересуют комплексные числа z =
х + yi, у которых х = -4. Это
уравнение прямой, параллельной оси ординат.
Слайд 11
б) Нас интересуют комплексные числа z = х
+ yi, у которых у = 2, 4,
6 или 8. Это множество состоит из четырех прямых, параллельных оси абсцисс.
Слайд 12
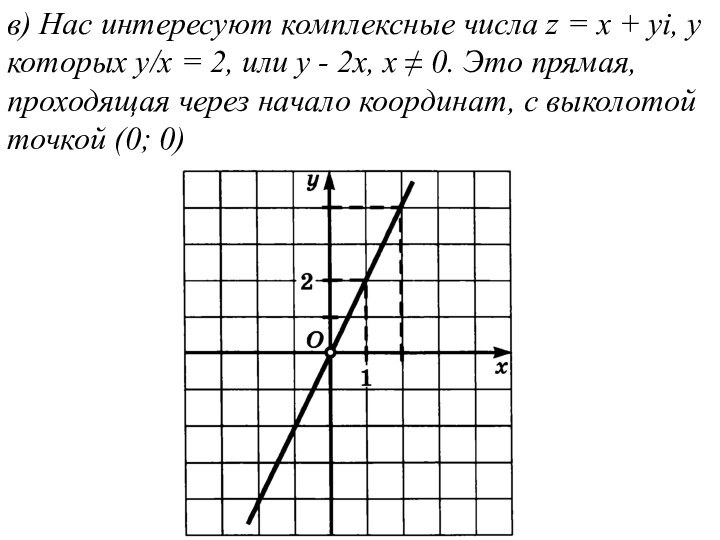
в) Нас интересуют комплексные числа z = x
+ yi, у которых y/x = 2, или у
- 2х, х ≠ 0. Это прямая, проходящая через начало координат, с выколотой точкой (0; 0)
Слайд 13
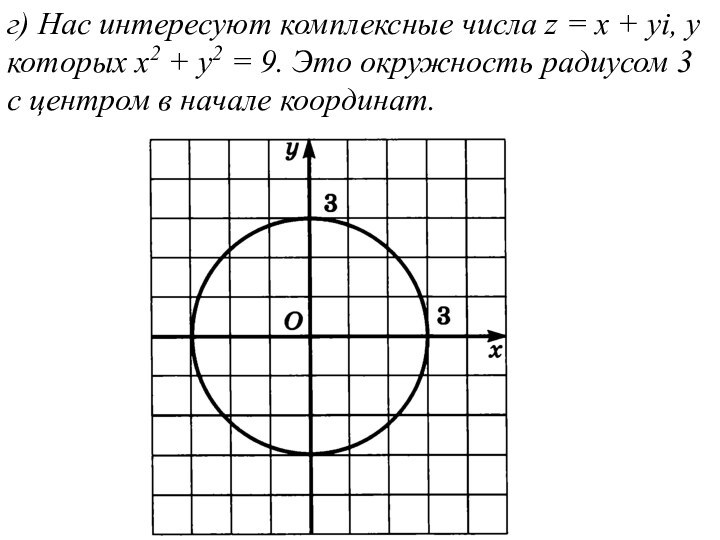
г) Нас интересуют комплексные числа z = х
+ yi, у которых х2 + у2 = 9.
Это окружность радиусом 3 с центром в начале координат.
Слайд 14
Любую точку на координатной плоскости можно воспринимать двояко:
алгебраически, как упорядоченную пару (а; b) действительных чисел, и
как вектор с началом в точке (0; 0) и концом в точке (а; b). При векторном подходе к изображению комплексных чисел наглядный смысл получают операции сложения и вычитания двух комплексных чисел:
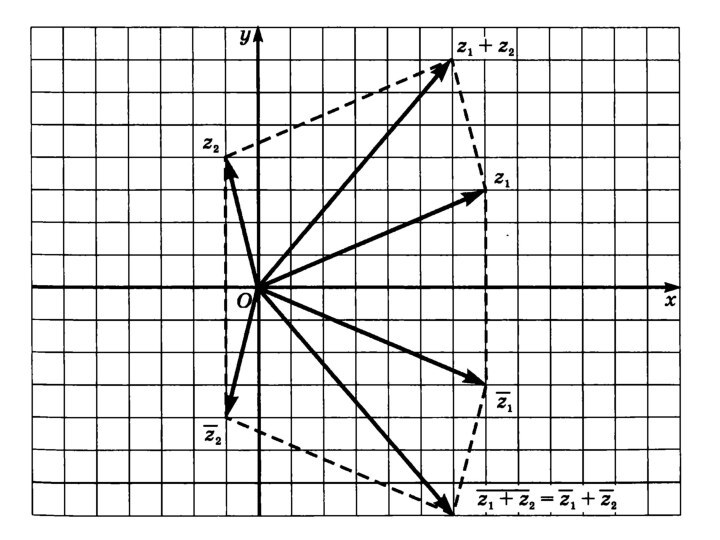
а) вектор, соответствующий сумме z1 + z2 двух комплексных чисел, равен сумме векторов, соответствующих числам z1 и z2;
б) вектор, соответствующий разности z1 - z2 двух комплексных чисел, равен разности векторов, соответствующих числам z1 и z2.
Слайд 15
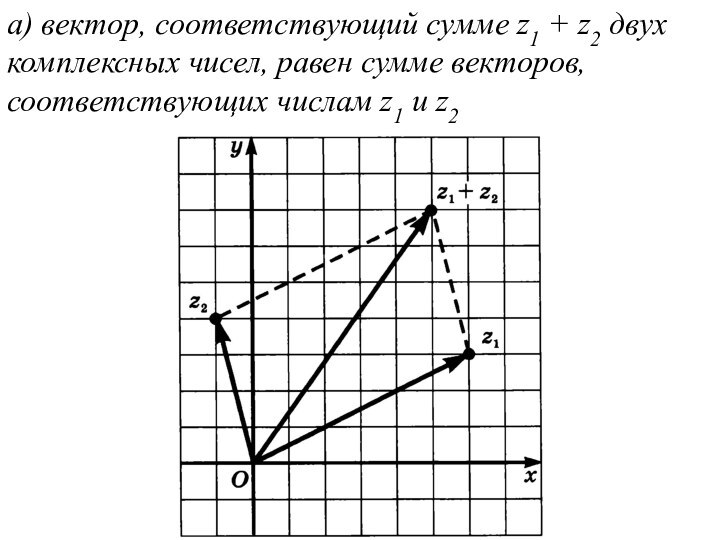
а) вектор, соответствующий сумме z1 + z2 двух
комплексных чисел, равен сумме векторов, соответствующих числам z1 и
z2
Слайд 16
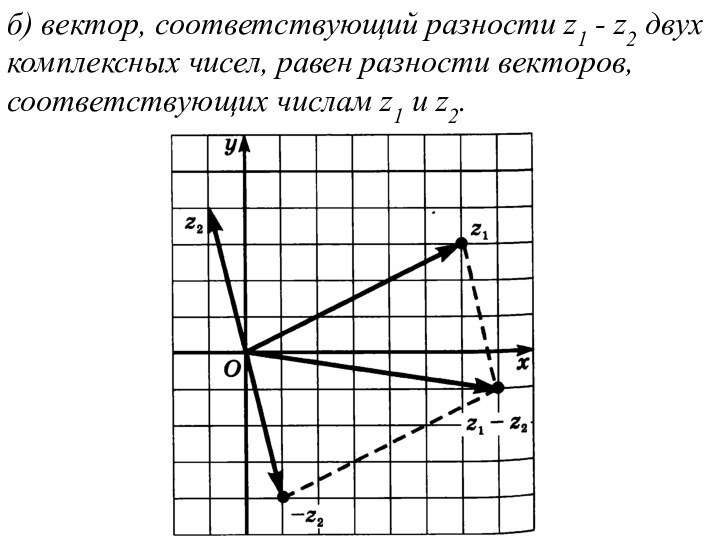
б) вектор, соответствующий разности z1 - z2 двух
комплексных чисел, равен разности векторов, соответствующих числам z1 и
z2.
Слайд 17
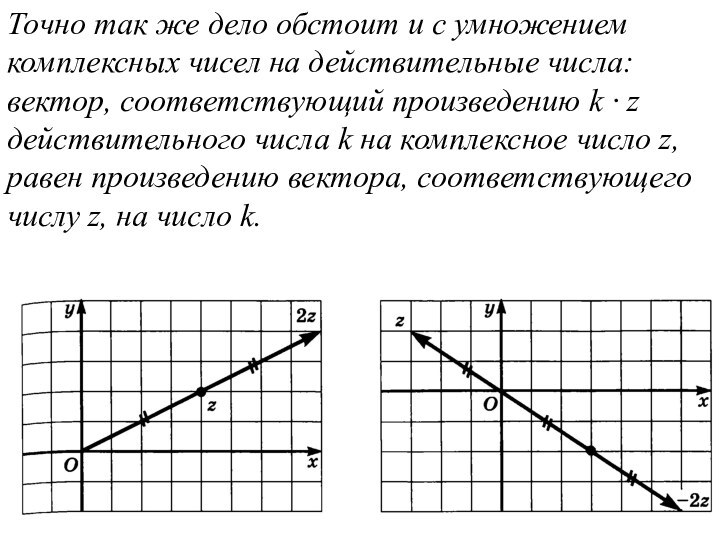
Точно так же дело обстоит и с умножением
комплексных чисел на действительные числа: вектор, соответствующий произведению k
∙ z действительного числа k на комплексное число z, равен произведению вектора, соответствующего числу z, на число k.
Слайд 18
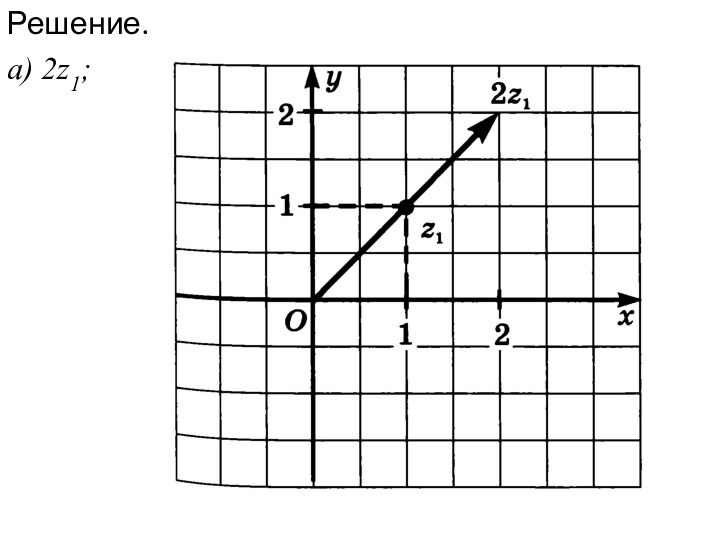
Пример 2. Для комплексных чисел z1 = 1
+ i и z2 = -1 + 2i изобразить
на координатной плоскости числа:
а) 2z1;
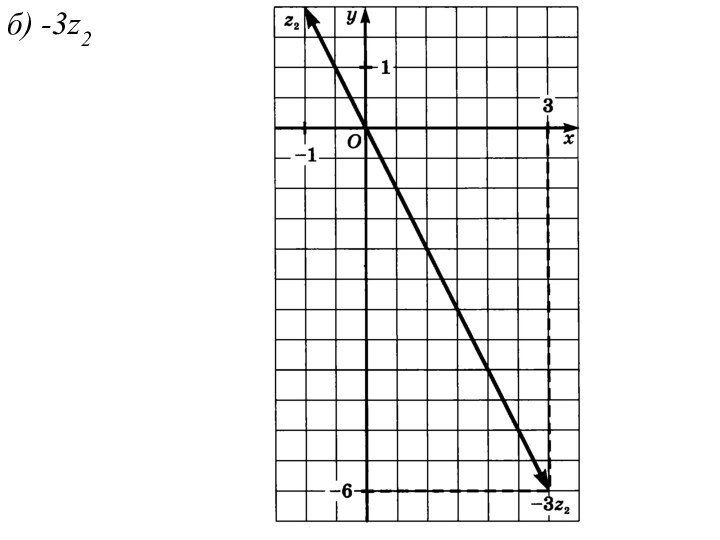
б) -3z2 ;
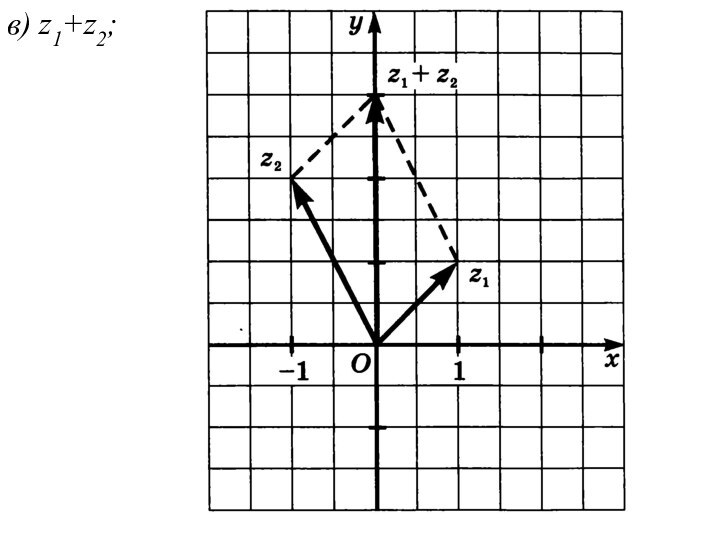
в) z1+z2;
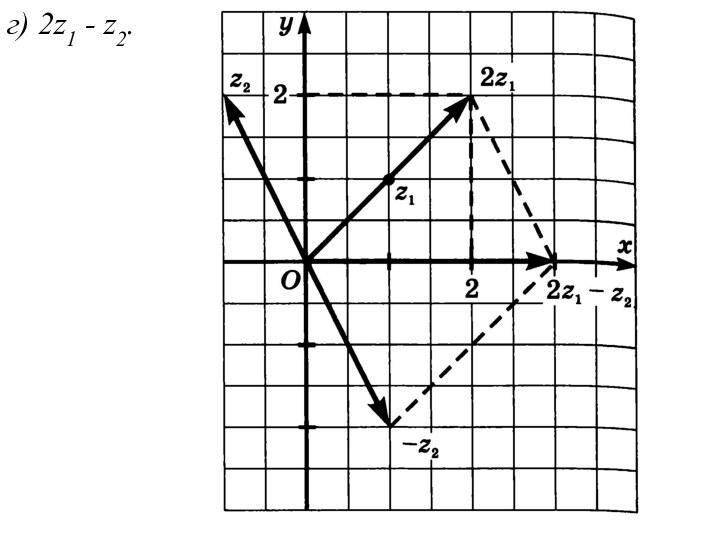
г) 2z1 - z2.
Слайд 23
Числа в заданиях можно найти по формулам, а
затем изобразить их на координатной плоскости.
Иногда приведенные правила
для сложения, вычитания комплексных чисел и умножения комплексных чисел на действительные числа объединяют таким образом: во множестве комплексных чисел операции сложения, вычитания и умножения на действительные числа производятся покоординатно. Подчеркнем, что сама эта формулировка предполагает операции уже не с самими комплексными числами, а с их геометрическими, векторными представениями.