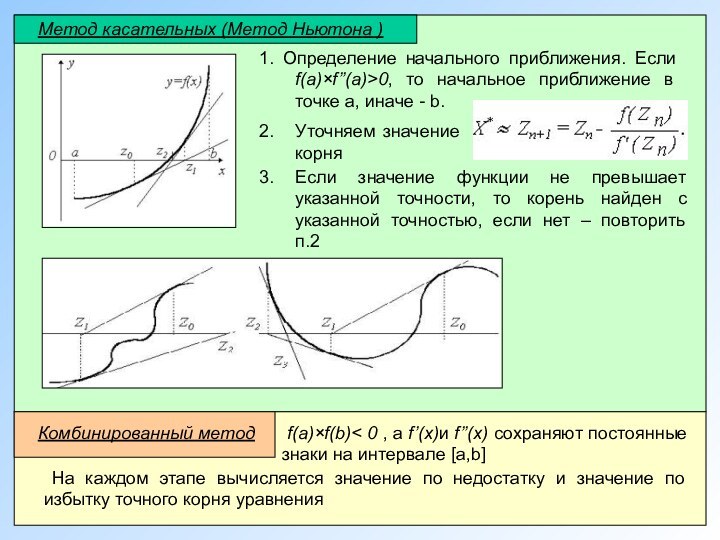
из 3-х уравнений с тремя неизвестными:
Матрица системы
Матрицы неизвестных
и свободных членов Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения на матрицу A-1, обратную матрице A
Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
A∙X=B
Матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных.











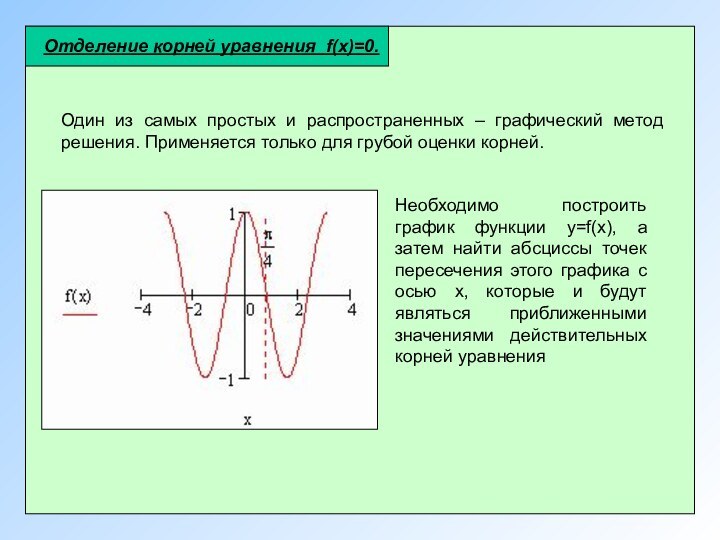
![Классификация уравнений. (Лекция 3) Уточнение корнейМетод половинного деления (дихотомии)Функция f(x)=0 непрерывна на отрезке [a,b] и f(a)×f(b)<](/img/tmb/15/1472289/eecdbaa242de1e01e1282cbe4ba43778-720x.jpg)