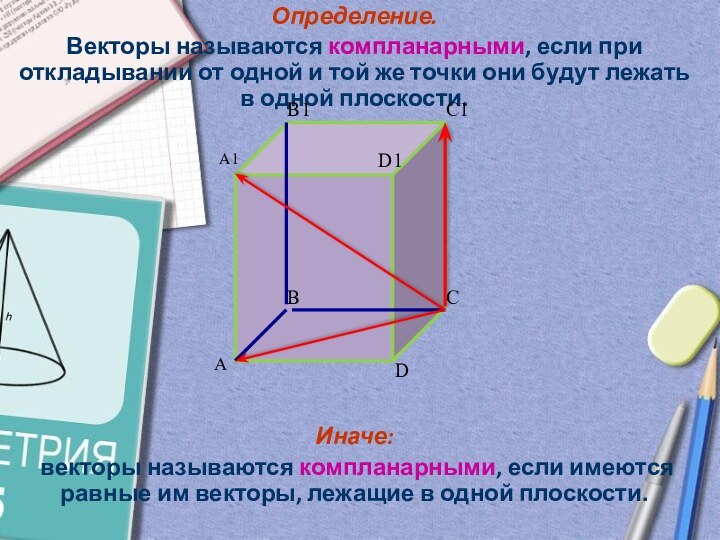
и той же точки они будут лежать в одной
плоскости.Иначе:
векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
A
B
C
D
A1
B1
C1
D1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

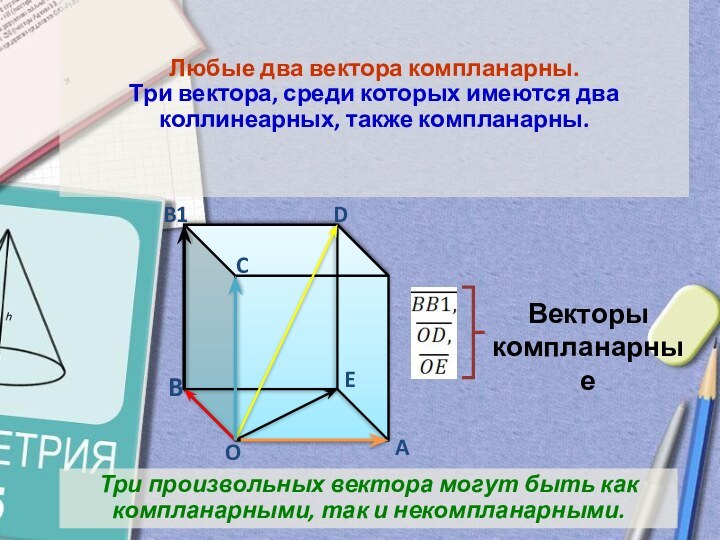




A
B
C
D
A1
B1
C1
D1
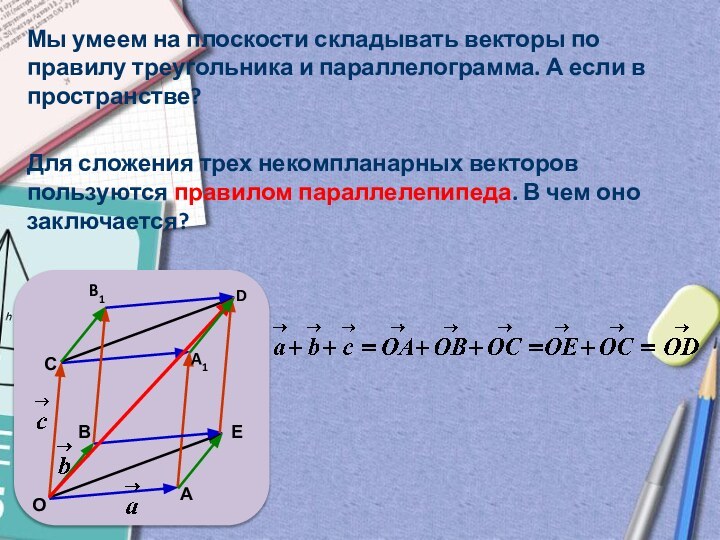
Е
С
В
А
О
D
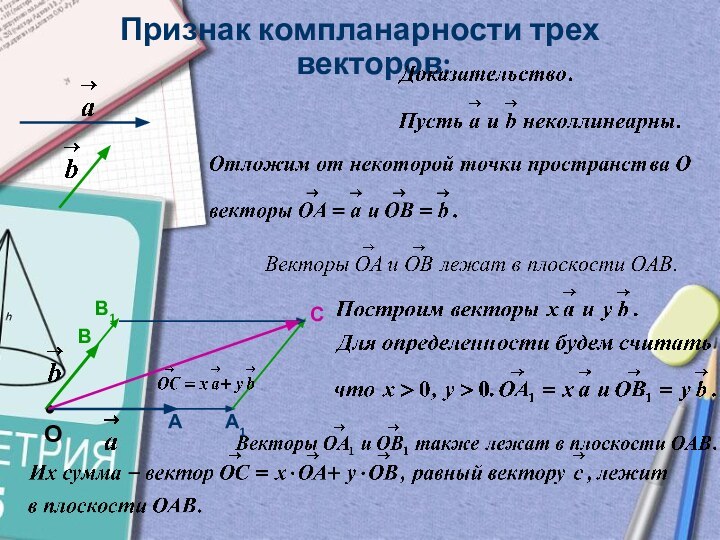
B1
A1