Презентация на тему Электрические свойства кристаллов

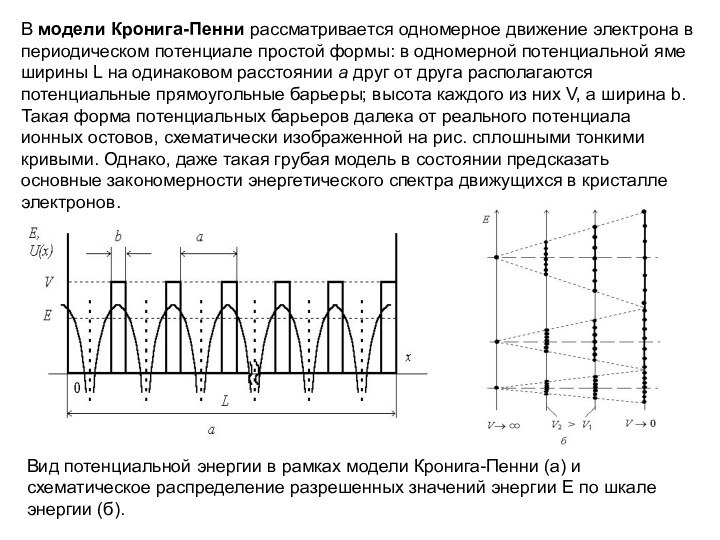
периодическом потенциале простой формы: в одномерной потенциальной яме ширины

L на одинаковом расстоянии a друг от друга располагаются потенциальные прямоугольные барьеры; высота каждого из них V, а ширина b. Такая форма потенциальных барьеров далека от реального потенциала ионных остовов, схематически изображенной на рис. сплошными тонкими кривыми. Однако, даже такая грубая модель в состоянии предсказать основные закономерности энергетического спектра движущихся в кристалле электронов.

Вид потенциальной энергии в рамках модели Кронига-Пенни (а) и схематическое распределение разрешенных значений энергии E по шкале энергии (б).

яме, может быть решено приближенными методами. В результате получается,

что энергия электрона может принимать не все значения. Промежуток на шкале Е, в котором нет разрешенных значений, называют запрещенной энергетической зоной, а промежуток, в котором имеются разрешенные значения, называют разрешенной энергетической зоной.
     При отсутствии барьеров задача аналогична задаче о движении электрона в одномерной потенциальной яме шириной L с периодическими граничными условиями для волновой функции. Распределение значений энергии электрона по шкале показано на рис. (б). Разрешенные значения энергии распределены по шкале без больших "пробелов".
Если барьеры настолько высокие и широкие, что туннелированием электрона сквозь них можно пренебречь, то задача аналогична задаче о движении электрона в одномерной потенциальной яме. Электрон окажется локализованным в этой маленькой потенциальной яме, при этом разрешенные значения изолированы друг от друга.
     При промежуточных значениях высот и ширин барьеров значения энергии вычисляют приближенными методами. В пределе при почти полной непроницаемости потенциальных барьеров разрешенная зона сужается почти до одиночного уровня. Такая ситуация характерна для изолированных атомов, в таком случае электрон локализован вблизи своего атома; это соответствует приближению сильной связи.

связи электрона в данном атоме больше энергии взаимодействия этого

электрона с полями, создаваемыми другими атомами.
     Приближение сильной связи хорошо описывает систему энергетических уровней электронов в случае атомов, хорошо удерживающих свои электроны, например в ионных и ковалентных кристаллах. Атомы воздействуют друг на друга создаваемыми ими электрическими и магнитными полями, эти поля приводят к расщеплению отдельного вырожденного уровня атома на несколько подуровней. В таком случае вместо одиночных уровней изолированных атомов в конденсированном веществе должен получиться большой набор уровней в некотором диапазоне энергий.
Для N атомов, расположенных далеко друг от друга, взаимодействием атомов можно пренебречь и считать, что каждый из них имеет определенные значения энергии уровней, одинаковые для каждого из атомов. Уровни всей системы N атомов окажутся 2N кратно вырожденными (из-за учета спина электрона). При сближении атомов энергия уровней будет уменьшаться за счет уменьшения энергии атомов из-за их взаимного притяжения. Кроме того, уровни будут расщепляться и тем сильнее, чем ближе находятся атомы, поскольку создаваемые ими поля возрастают при приближении к атому. При расстоянии между атомами порядка периода кристаллической решетки должен наблюдаться минимум энергии уровней, поскольку при дальнейшем сближении атомы отталкиваются, и энергия их взаимодействия сильно возрастает.

между ними.
Модель почти свободных электронов. Существует большая группа

кристаллических веществ, например металлических, в которых внешние электроны атомов "обобществляются" и могут относительно свободно перемещаться по кристаллу. В этом случае очень удачной оказывается модель почти свободных электронов, в рамках которой считают, что электроны в кристалле движутся внутри потенциальной ямы размером с кристалл в слабом поле периодически расположенных ионных остовов, которое можно рассматривать как малое возмущение.

в кристалле полем ионных остовов пренебрегают и используют модель

электронного Ферми-газа.  Систему электронных состояний в пространстве волновых векторов электронов получают в результате решения уравнения Шредингера для трехмерного потенциального ящика кубической формы с ребром длины L. В случае периодических граничных условий для волновой функции Ψ система электронных состояний имеет допустимые значения волнового вектора

где n1, n2, n3 - целые числа. Шаг изменения величин kx, ky, kz оказывается малым из-за большой величины L. Поэтому функции зависящие от k далее рассматриваются как непрерывные.

Волновые функции электронов имеют вид:

Кинетическая энергия электронов вычисляется по формуле:

с самыми малыми значениями энергии, соблюдая принцип Паули (не

более 1 электрона на одно состояние). В таком случае в k-пространстве занятые состояния окажутся внутри шара радиуса kF. Поверхность этого шара называется поверхностью Ферми, а отвечающая ей энергия электронов - энергией Ферми. Энергия Ферми зависит от концентрации свободных электронов n и вычисляется по формуле:

При увеличении температуры вероятность заполнения состояний электронами задается функцией занятости состояний, имеющей вид:

Функция заполнения состояний электронами Ферми-газа при различных температурах.

их плавления, энергия Ферми в 50-200 раз превосходит величину

kT. Поэтому электронный газ в металлах рассматривают как сильно вырожденный электронный Ферми-газ. Энергия Ферми при увеличении температуры незначительно увеличивается и задается формулой:

Таким образом, увеличение температуры ведет к незначительному размытию поверхности Ферми в k-пространстве.

Потенциал ионных остовов в модели почти свободных электронов рассматривается как периодическая функция с периодами, соответствующими параметрам кристаллической решетки, для нее выполняется соотношение:

при появлении периодического поля с потенциальной энергией вида изменяется

в соответствии с формулой:

периодическая функция, имеющая те же периоды, что и потенциальная энергия ионных остовов (по сути – период решетки)

В приближении почти свободных электронов считают, что uk(r) почти во всем пространстве внутри кристалла близка к единице, и только в малых областях "внутри" ионных остовов она заметно отличается от единицы.

Наиболее значимые особенности функции E(k) наблюдаются вблизи границы зоны Бриллюэна. Рассмотрим простую кубическую кристаллическую решетку с периодом a. Пусть электрон движется по направлению [100] и имеет волновой вектор k=(k;0;0) (а). Если бы мы пренебрегли полями ионных остовов, то получили бы квадратичную зависимость энергии от волнового вектора, изображенную на рис. (б).

с периодом а и образования стоячей волны в этой

решетке (а). Зависимость энергии электрона от его волнового вектора в модели свободных электронов и в модели почти свободных электронов (б)

Электрон обладает волновыми свойствами, в частности имеет длину волны де-Бройля равную

границах зон Бриллюэна, т.е. при волновом числе, соответствующем границе

зон Бриллюэна, волны перестают распространяться в кристалле. В одномерном случае отражение волн наступает при

Полное отражение волны означает, что вместо бегущих волн вида exp(ikx) стационарным состояниям электрона при значениях k=πn/a отвечают стоячие волны. Падающая и отраженная волна может складываться двумя способами, образуя cимметричную и антисимметричную комбинации:

Волновым функциям Ψ1 и Ψ2 соответствуют разные значения энергии, причем E11.

в приближении сильной связи и в приближении почти свободных

электронов качественно совпадают. Различие состоит только в том, что в первом случае возникают узкие разрешенные зоны и широкие запрещенные зоны. Во втором случае наоборот, получаются широкие разрешенные зоны и узкие зоны запрещенных энергий. В реальных кристаллах наблюдаются как эти предельные случаи, так и промежуточные варианты. Однако во всех случаях энергетический спектр электронов в кристалле имеет зонную структуру, причем в пределах каждой зоны энергия меняется почти непрерывно. Вместо классического случая, в котором электроны либо принадлежат отдельным атомам, либо движутся свободно до первого столкновения с атомным остовом, квантовая динамика приводит к качественно иному результату. В случае с идеальной решеткой каждый электрон способен двигаться свободно, не меняя энергию, если только эта энергия принадлежит определенной разрешенной зоне.

кристаллической решетки не меняет радикально картину движения электрона по

сравнению его движением в свободном пространстве.

Соотношение неопределенностей:

волновой функцией свободного электрона является плоская волна вида:

Скорость распространения максимума амплитуды волнового пакета, так называемая групповая скорость:

Рассмотрим движение электрона как классической частицы под действием внешней силы F, вычислим, как будет изменяться групповая скорость.

закону Ньютона, если положить, что:

Величину mэ называют эффективной массой

электрона. В ее значении косвенно учтено воздействие периодического поля кристалла, на закон изменения энергии электрона от волнового вектора электрона.
При малых значениях k, ее значение, задаваемое второй производной функции E(k), оказывается положительным, а при k близких к границе зоны Бриллюэна - отрицательным. В последнем случае получается, что внешняя сила не ускоряет, а тормозит электрон. Это связано с влиянием периодического поля кристалла на движение электрона. Такие электроны ведут себя во внешних электромагнитных полях как частицы с отрицательной массой или как положительно заряженные частицы.
          Для большей части электронов эффективная масса как правило положительна. В частности, она положительна у всех электронов, если зона заполнена наполовину или менее. Отрицательной эффективной массой обладают лишь электроны в состояниях вблизи границы первой зоны Бриллюэна.