Область определения
Множество
значенийЧетность и нечетность
3. Задачи с параметром
4. Задачи из сборника ЕГЭ, часть «С»
5. Использованные источники
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

















Как начинать решать такие задачи?
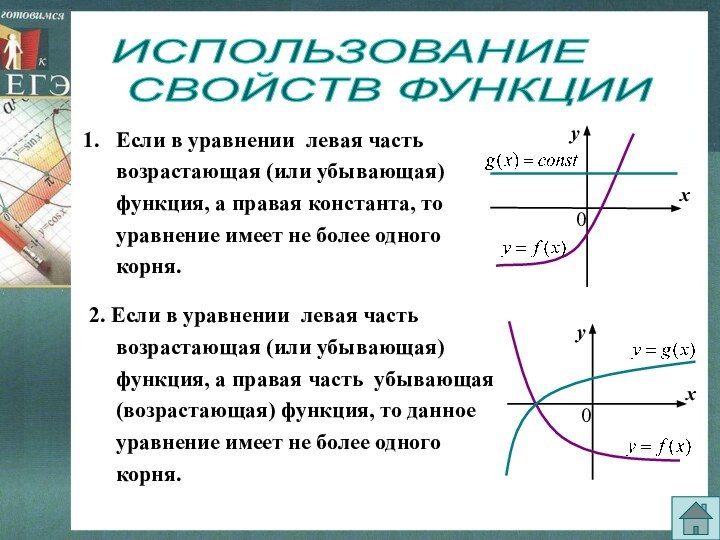
МЕТОД МАЖОРАНТ
Привести уравнение или неравенство к виду
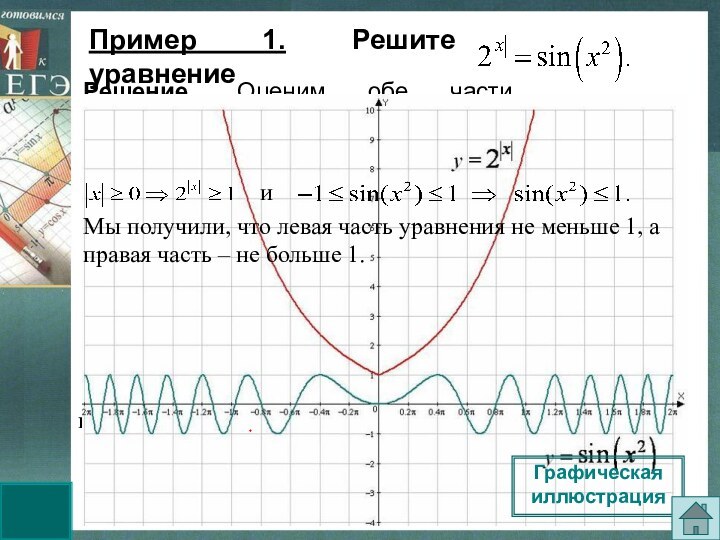
Графическая иллюстрация
Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1.
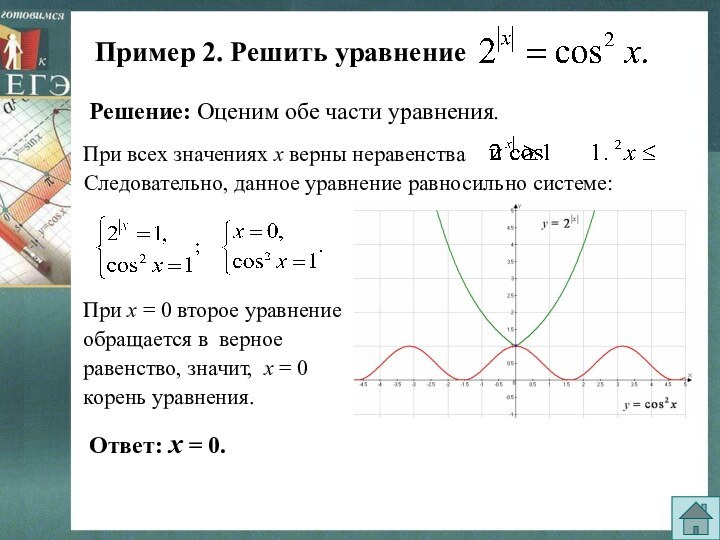
Ответ: х = 0.
Ответ: - 1.
Решение.
Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства.
Пример 4. Решить уравнение
Для правой части (в силу неравенства для суммы двух взаимно
обратных чисел) выполнено
Поэтому уравнение имеет решения, если и только если
одновременно выполнены два условия
принимает значение от 0,5 до 2
Решение. Оценим обе части уравнения.
Решение. Оценим обе части уравнения.
1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение.
Значит, данное уравнение равносильно системе уравнений:
Решая систему уравнений, получаем решения исходного уравнения:
.
Заметим, что перемножив
Ответ:
?
сумма двух положительных взаимообратных чисел
?
?
сумма единицы и неотрицательного числа
sin 3z ∈[-1;1] ⇒ 3 + sin3z ∈[2; 4].
Поэтому равенство возможно
только при условии:
Сначала решим второе уравнение:
Корни этого уравнения
Итак, данное уравнение имеет единственный корень х = 0.
Ответ: 0.
При х = -1 имеем:
?
?
cos(α)∈[-1;1] ⇒ cos2(α )∈[0; 1].
сумма единицы и неотрицательного числа.
При всех значениях х выражение:
При всех значения х выражение:
поэтому
Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему:
Решение. Перепишем уравнение в виде
Оценим функции входящие в данное уравнение.
Очевидно, что
х
у
0
х
у
0
?
?
?
?
?
Решить уравнение:
Решение.
Второй радикал определен при любых значениях х.
Выражение под третьим радикалом неотрицательно если
Ответ: 1.
Ответ: ∅.
Решение.
2) Проверим не отрицательность правой части:
Последнее неравенство решений не имеет.
Ответ: 1250.
Решение.
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИ
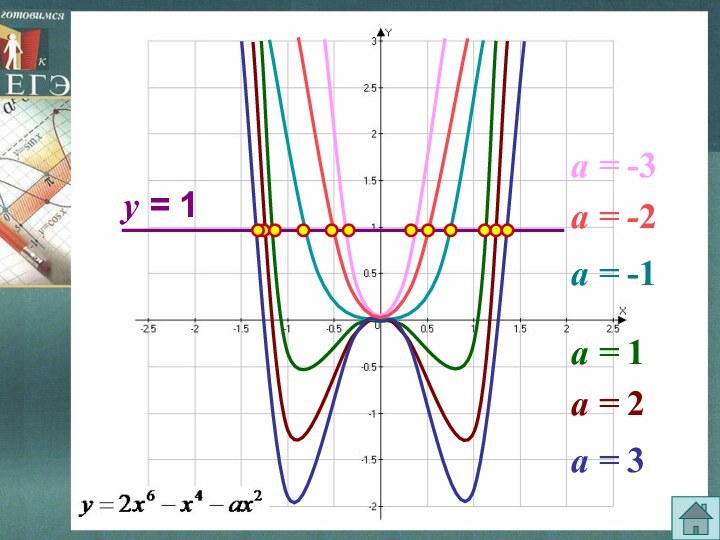
Так как число 0 не является корнем уравнения, то уравнение имеет четное число корней.
Ответ: не может.
Графическая иллюстрация
иметь нечетное число корней?
Решение.
Ответ: да.
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИ