- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Линейное программирование
Содержание
- 2. Жордановы исключения названы по имени известного французского
- 3. Пусть рассматривается система yi = ai1* x1 + ai2 * x2 +
- 4. Такое табличное представление системы (1.1) позволяет в
- 5. Итак, будем называть шагом обыкновенного жорданова исключения,
- 6. Новая таблица будет иметь видгде b i j = a i
- 7. Новая таблица (1.4) получена из таблицы (1.2)
- 8. ПримерВ системе y1 = x1 – 2*x2,y2 = - x1 + x2 +2*x3,y3 =
- 9. Запишем исходную систему в виде жордановой таблицы:Выполнив
- 10. Модифицированные жордановы исключения В некоторых конкретных задачах,
- 11. Один шаг модифицированного жорданова исключения с разрешающим элементом ars означает
- 12. ПримерСистему y1 = 2x1 – x2 +3x3,y2 = - x1 + 4x2 -2*x3,y3 = 5*x1 + 2x2 – 4x3 запишем в виде таблицы
- 13. Скачать презентацию
- 14. Похожие презентации
Жордановы исключения названы по имени известного французского математика Камиля Жордана (1838-1922 гг.), внесший существенный вклад в развитие алгебры, теории функций и топологии.










Слайд 3
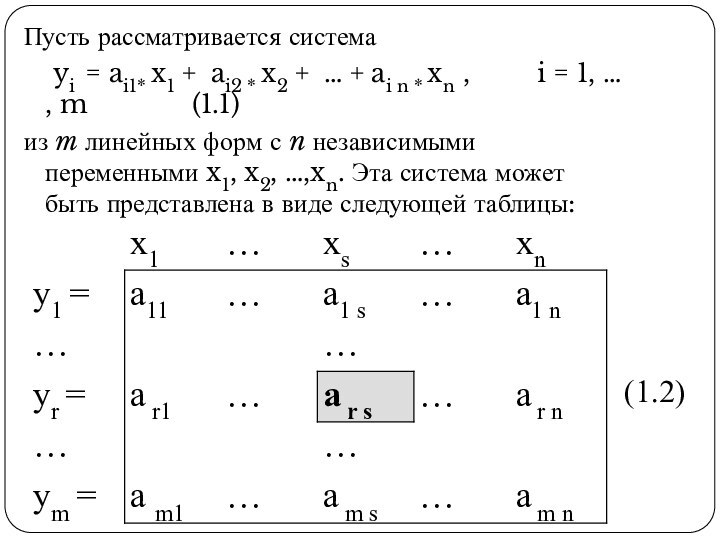
Пусть рассматривается система
yi = ai1* x1 + ai2 * x2 + …
+ ai n * xn , i = 1, … ,
m (1.1)из m линейных форм с n независимыми переменными x1, x2, …,xn. Эта система может быть представлена в виде следующей таблицы:
Слайд 4 Такое табличное представление системы (1.1) позволяет в дальнейшем
производить различные действия над системой схематизировано, т.е. осуществлять пересчет коэффициентов
таблицы аij по определенному алгоритму, а именно с помощью аппарата жордановых исключений.Пусть, например, возникла необходимость выразить независимую переменную xs из уравнения
yr = a r1 * x1 + a r2 * x2 + … a rs * xs + … + a r n * xn , (1.4)
где yr является переменной, которая зависит от переменных x1, x2, …, xn, и подставить полученное выражение во все остальные уравнения системы (1.2). Эту операцию можно выполнить по определенной схеме, которая достаточно просто алгоритмизируется.
Слайд 5 Итак, будем называть шагом обыкновенного жорданова исключения, произведенным
над таблицей (1.2) с разрешающим элементом a rs ≠ 0 с r-ой
разрешающей строкой и s-ым разрешающим столбцом, схематизированную операцию перемены ролями между зависимой переменной yr и независимой xs, т.е. операцию решения уравнения (1.3) относительно xs, подстановки полученного выражения во все остальные уравнения системы (1.1) и записи полученной системы в виде новой таблицы, аналогичной (1.2).
Слайд 6
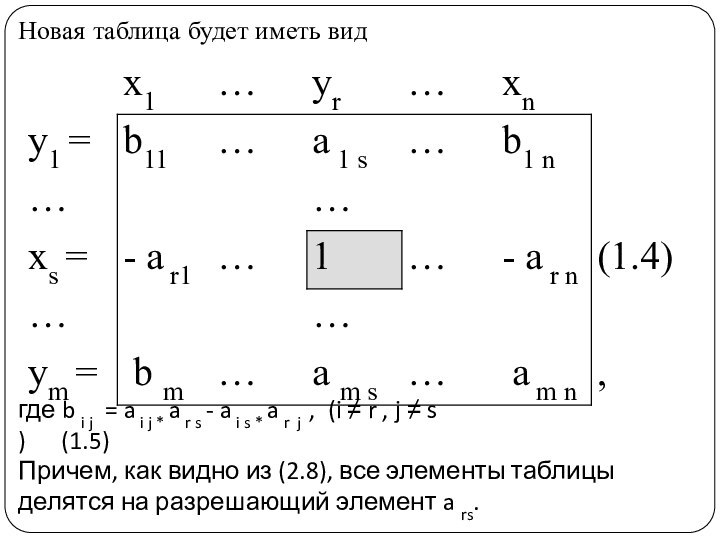
Новая таблица будет иметь вид
где b i j = a i j
* a r s - a i s * a r j , (i ≠ r
, j ≠ s ) (1.5)Причем, как видно из (2.8), все элементы таблицы делятся на разрешающий элемент a rs.
Слайд 7 Новая таблица (1.4) получена из таблицы (1.2) по
следующей схеме (СХЕМА 1):
1) разрешающий элемент заменяется единицей и делится
на разрешающий элемент;2) остальные элементы разрешающего (s - го) столбца делятся на разрешающий элемент;
3) остальные элементы разрешающей (s - ой) строки меняют свой знак на противоположный и делятся на разрешающий элемент;
4) все остальные элементы таблицы вычисляются по формуле (1.5) и делятся на разрешающий элемент a rs; формула (1.5) иногда называется "правилом прямоугольника", так как схема вычисления элемента bij соответствует вычислению разности произведений элементов, стоящих по основной и побочной диагоналям прямоугольника, образованного в таблице вида (1.2) всеми элементами, вошедшими в формулу (1.5).
Слайд 8
Пример
В системе
y1 = x1 – 2*x2,
y2 = - x1 + x2 +2*x3,
y3 = 2*x1 –
x2 – x3
необходимо поменять ролями переменные x3 и y2, т.е.
сделать зависимую переменную y2 независимой, а независимую переменную x3 зависимой.
Слайд 9
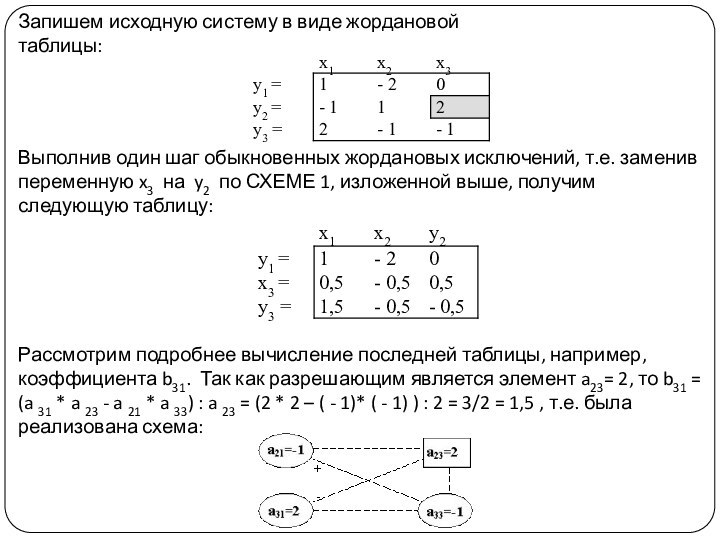
Запишем исходную систему в виде жордановой таблицы:
Выполнив один
шаг обыкновенных жордановых исключений, т.е. заменив переменную x3 на
y2 по СХЕМЕ 1, изложенной выше, получим следующую таблицу:Рассмотрим подробнее вычисление последней таблицы, например, коэффициента b31. Так как разрешающим является элемент a23= 2, то b31 = (a 31 * a 23 - a 21 * a 33) : a 23 = (2 * 2 – ( - 1)* ( - 1) ) : 2 = 3/2 = 1,5 , т.е. была реализована схема:
Слайд 10
Модифицированные жордановы исключения
В некоторых конкретных задачах, например, в
вычислительной схеме симплекс-метода, бывает удобно независимые переменные представлять в
таблице со знаком "минус". В этих случаях имеет смысл вместо обыкновенных использовать так называемые модифицированные жордановы исключения.Перепишем систему (1.1) в виде эквивалентной ей системы:
yi = -ai1*(-x1) - ai2 *(- x2)- … - ai n *(- xn) , i = 1, … , m.
Составим по полученной системе таблицу, учитывая минус при переменных хj наверху таблицы:
Слайд 11 Один шаг модифицированного жорданова исключения с разрешающим элементом ars означает переход
к новой таблице:
Эта таблица формируется по СХЕМЕ 2, которая очень напоминает
схему обыкновенных жордановых исключений, в ней меняются только 2 и 3 пункты, а именно:2) остальные (кроме разрешающего) элементы разрешающей строки делятся на разрешающий элемент;
3) остальные элементы разрешающего столбца меняют свой знак на противоположный и делятся на разрешающий элемент.





























