- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Преобразование подобия и его свойства
Содержание
- 2. Преобразование подобия и его свойства. Подобные фигуры
- 3. Цели урока:-узнать какое преобразование называется подобием;-какими свойствами
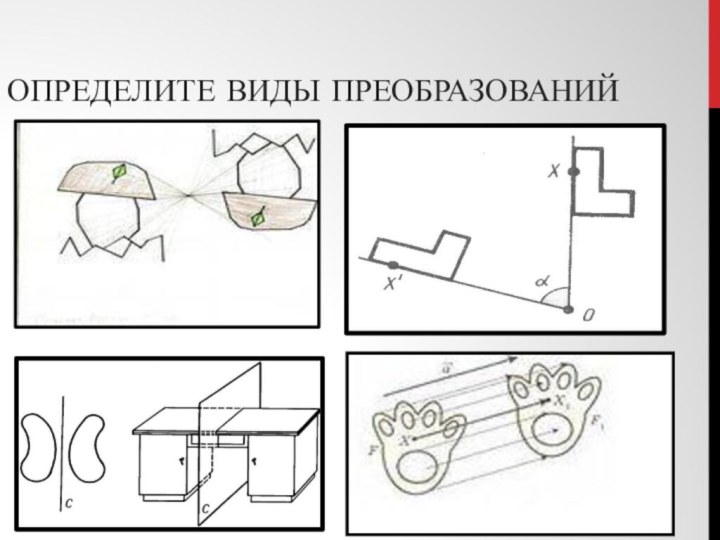
- 4. Определите виды преобразований
- 5. Вопрос!Какого преобразования не было среди перечисленных?
- 6. Гомотетия!Определение гомотетии;Свойства гомотетии;Элементы гомотетии;Является ли гомотетия движением?
- 7. Работа по карточкам:Задание 1.Дан треугольник АВС, точка
- 8. Преобразование подобия.
- 9. Подобие вокруг нас!
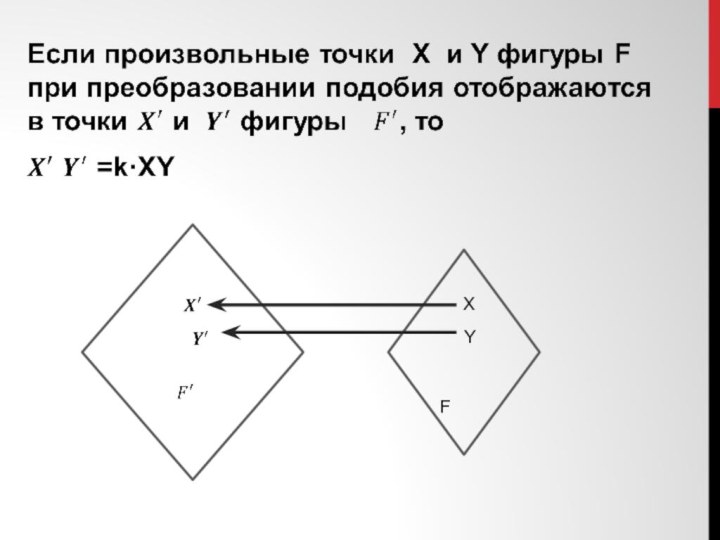
- 11. XFY
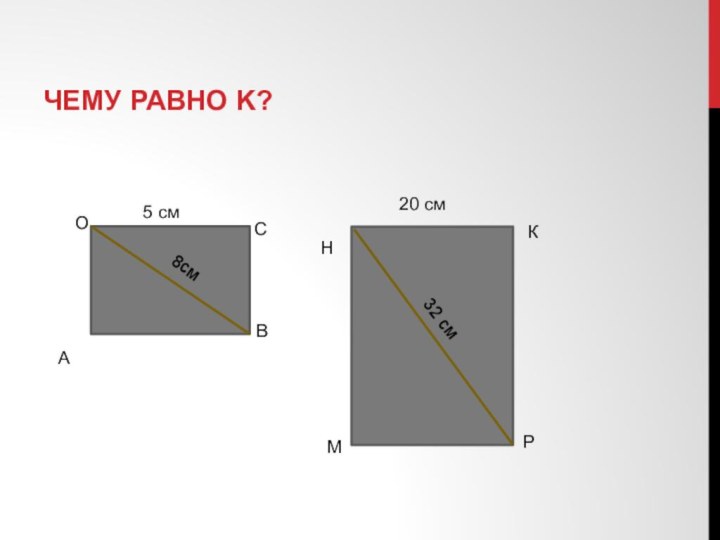
- 12. Чему равно K?
- 14. Вопрос!Если k=1, то преобразование подобия будет являться каким преобразованием?
- 15. Задание:Если размеры фигуры, полученной преобразованием подобия относительно
- 17. Свойства преобразования подобияСвойство 1:Преобразование подобия переводит прямые
- 19. Подобные фигурыДве фигуры называются подобными, если они переводятся друг в друга преобразованием подобия
- 20. Подобные фигурыРасстояние между соответствующими точками изменилось в
- 21. Свойства подобных фигурЕсли фигура А подобна фигуре
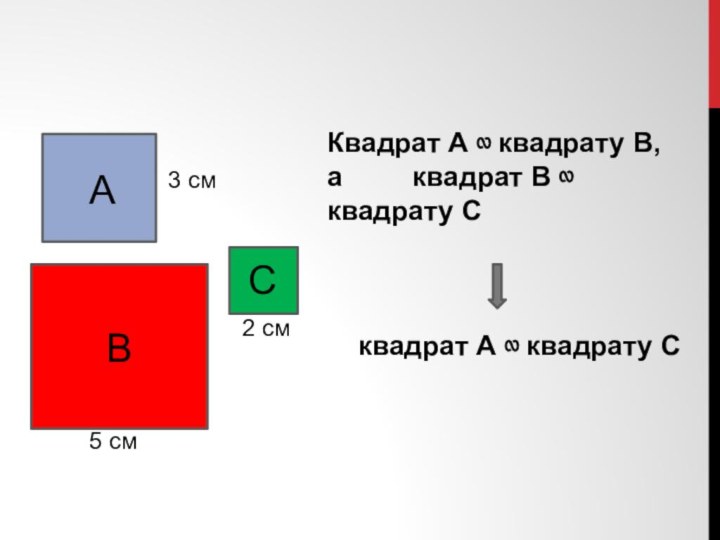
- 22. Квадрат А ∾ квадрату В, а
- 23. ∆АВС ∾ ∆КМН∠
- 24. Попробуй сам!Задание 1. Дан квадрат АВСD, сторона
- 25. Задание 3 Дано: ∆АВС ∾ ∆МРН
- 26. Домашнее задание.Параграф 17, учить определения, № 168
- 27. Скачать презентацию
- 28. Похожие презентации
Преобразование подобия и его свойства. Подобные фигуры























Слайд 3
Цели урока:
-узнать какое преобразование называется подобием;
-какими свойствами обладает
подобие;
Слайд 6
Гомотетия!
Определение гомотетии;
Свойства гомотетии;
Элементы гомотетии;
Является ли гомотетия движением?
Слайд 7
Работа по карточкам:
Задание 1.
Дан треугольник АВС, точка О-центр
гомотетии, коэффициент гомотетии равен 2. Постройте треугольник гомотетичный данному.
Задание
2.Дан параллелограмм АВСD, точка О-центр гомотетии, коэффициент гомотетии равен 1,5. Постройте параллелограмм гомотетичный данному.
Задание 3.
Дана трапеция АВСD, точка О-центр гомотетии, коэффициент гомотетии равен -2. Постройте трапецию гомотетичную данной.
Слайд 15
Задание:
Если размеры фигуры, полученной преобразованием подобия относительно исходной,
увеличились в 7 раз, то чему равен коэффициент подобия?
А
если уменьшились в 10 раз, то тогда коэффициент подобия чему равен?
Слайд 17
Свойства преобразования подобия
Свойство 1:
Преобразование подобия переводит прямые в
прямые, полупрямые в полупрямые, отрезки в отрезки;
Свойство 2:
Преобразование подобия
сохраняет углы между полупрямыми
Слайд 19
Подобные фигуры
Две фигуры называются подобными, если они переводятся
друг в друга преобразованием подобия
Слайд 20
Подобные фигуры
Расстояние между соответствующими точками изменилось в одно
и то же число раз, значит, треугольники были подвергнуты
преобразованию подобия, следовательно треугольники подобны:∆АВС∾∆А1В1С1
число 3 – коэффициент подобия
∾ - знак подобия фигур
А
А1
С
В
С1
В1
5см
15см
4см
12см
6 см
18 см
Слайд 21
Свойства подобных фигур
Если фигура А подобна фигуре В,
а фигура В подобна фигуре С, то фигуры А
и С подобны;У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны.
Слайд 23
∆АВС ∾ ∆КМН
∠ А=∠
К, ∠В=∠М, ∠С=∠Н
и АВ:КМ=ВС:МН=АС:КН
Против равных углов лежат пропорциональные стороны
А
С
В
К
Н
М
Слайд 24
Попробуй сам!
Задание 1.
Дан квадрат АВСD, сторона которого
равна 2 см , коэффициент подобия равен 4, постройте
квадрат подобный данному.Задание 2.
Стороны подобного данному параллелограмма KMNE равны KM=NE=15, MN=KE=27, к=3, найдите стороны исходного параллелограмма FSRT.





























