- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему дополнительный материал по математике 5-8 класс на тему Системы счисления
Содержание
- 2. Дешифровка цифровых знаков Дешифровка цифровых знаков майя
- 3. Мудрость народаМожно лишь без конца изумляться великой
- 4. Ноль и бесконечность Чванливая Европа еще считала
- 5. число 20 ? Древние майя пользовались двадцатеричной системой счисления
- 6. Почему 20?На помощь приходит простая логика. Она
- 7. «виналь»Подтверждение именно такому объяснению возникновения двадцатеричной системы
- 8. «один человек» - число 20 По-видимому, говоря
- 9. одно из замечательных достижений человеческого разума.
- 10. на целое тысячелетие (!) раньше Древние майя
- 11. этажерка из цифр Однако запись цифровых знаков,
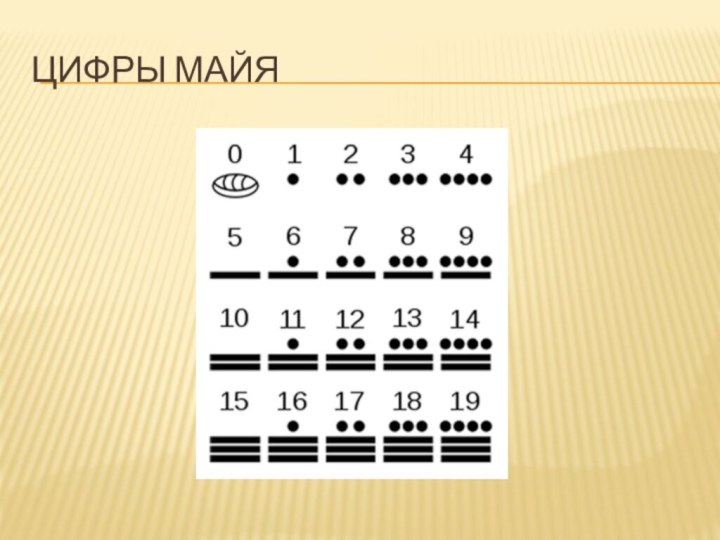
- 12. Цифры майя
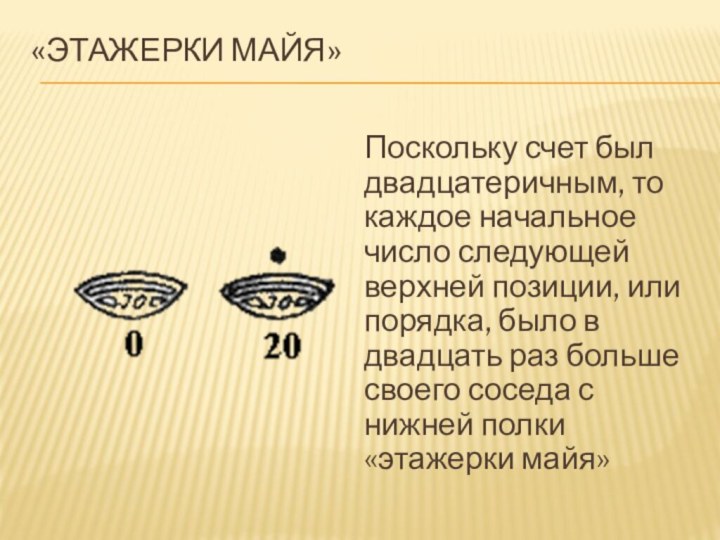
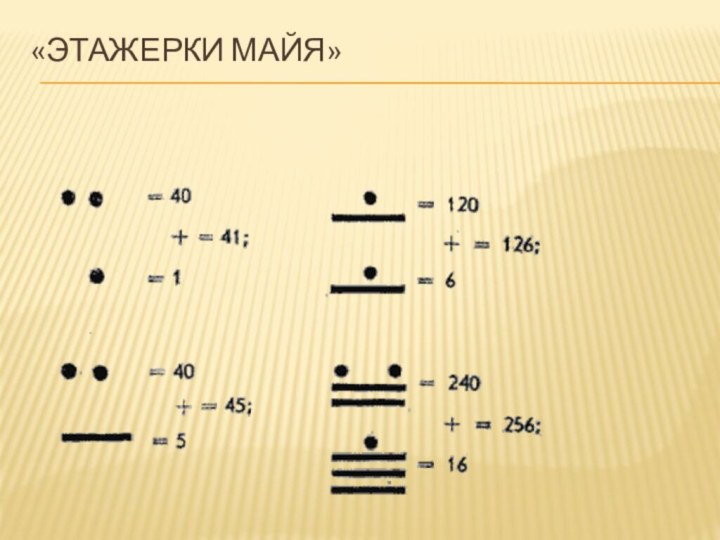
- 13. «этажерки майя» Поскольку счет был двадцатеричным,
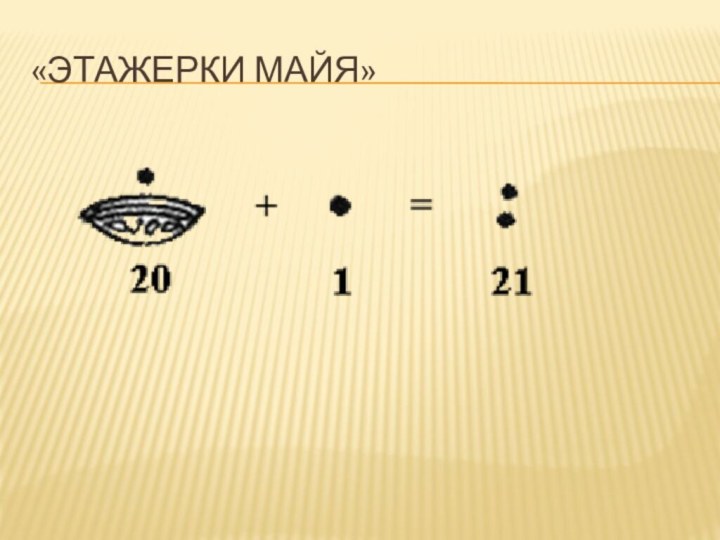
- 14. «этажерки майя»
- 15. «этажерки майя» На первой полке стояли
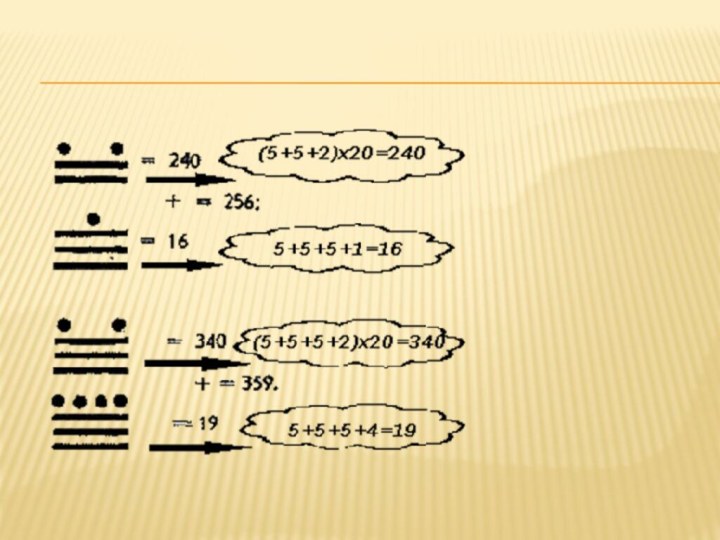
- 16. «этажерки майя»
- 17. «этажерки майя»
- 18. исключениеВ двадцатеричной системе счета древних майя есть
- 19. Исключение Суть его сводится к следующему: 360
- 20. принцип двадцатеричности нарушен! начальное число третьего порядка
- 21. Зачем??? А вызвано оно — что самое
- 22. Приспособили абстрактность математикиМайя не побоялись нарушить строгий,
- 23. Календарный годМайя максимально приблизили первоначальное число третьего
- 24. Майя – великая цивилизацияТак, начав с конкретного
- 25. до бесконечно больших величинПри образовании чисел четвертой
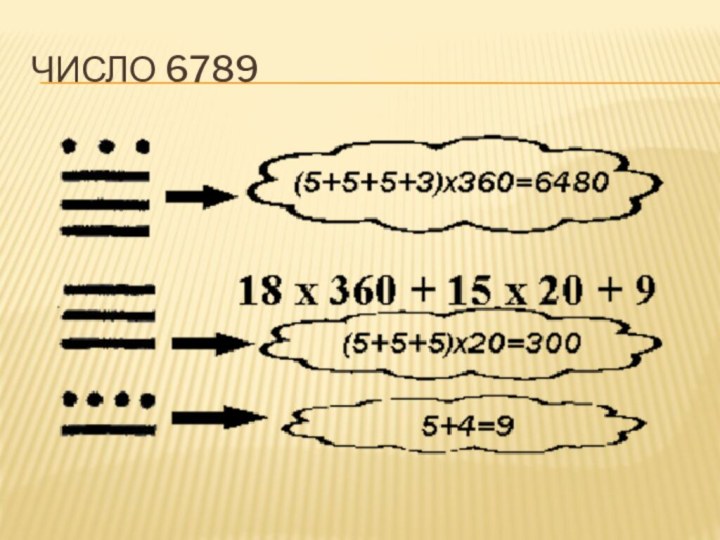
- 27. Как записать число 6789
- 28. число 6789
- 31. Скачать презентацию
- 32. Похожие презентации
Дешифровка цифровых знаков Дешифровка цифровых знаков майя не составила большого труда для ученых. Причиной тому поразительная простота и доведенная до совершенства логичность системы их счета.

























Слайд 3
Мудрость народа
Можно лишь без конца изумляться великой мудрости
народа, сумевшего практически в одиночку подняться на недоступные вершины
абстрактного математического мышления, одновременно приспособив его к своим конкретно-практическим земным нуждам.
Слайд 4
Ноль и бесконечность
Чванливая Европа еще считала по
пальцам, когда математики древних майя ввели понятие нуля и
оперировали бесконечно большими величинами
Слайд 6
Почему 20?
На помощь приходит простая логика. Она подсказывает,
что скорее всего сам человек был для древних майя
той идеальной математической моделью, которую они и взяли за единицу счета.
Слайд 7
«виналь»
Подтверждение именно такому объяснению возникновения двадцатеричной системы счета
находится в этимологической связи слова «виналь» (так на языке
майя назывался двадцатидневный месяц) со словами «двадцать» и «человек».
Слайд 8
«один человек» - число 20
По-видимому, говоря «один
человек», древние майя механически представляли себе число 20, если,
конечно, в это время речь шла о каких-то количественных единицах.
Слайд 9
одно из замечательных достижений человеческого разума.
Мы, пользуемся
так называемой арабской цифровой системой, (V век). В соответствии
с этой системой мы расставляем цифровые знаки горизонтально-строчечным способом, применяя «позиционный принцип» — одно из замечательных достижений человеческого разума.
Слайд 10
на целое тысячелетие (!) раньше
Древние майя также
пришли к использованию позиционного принципа. В отличие от нас,
европейцев, им не у кого было заимствовать этот принцип, и они сами додумались до него, причем почти на целое тысячелетие (!) раньше Старого Света.
Слайд 11
этажерка из цифр
Однако запись цифровых знаков, образующих число,
они стали вести не горизонтально, а вертикально, снизу вверх,
как бы возводя некую этажерку из цифр.
Слайд 13
«этажерки майя»
Поскольку счет был двадцатеричным, то каждое
начальное число следующей верхней позиции, или порядка, было в
двадцать раз больше своего соседа с нижней полки «этажерки майя»
Слайд 15
«этажерки майя»
На первой полке стояли единицы, на
второй — двадцатки и т. д.(если бы майя пользовались
десятеричной системой, то число было бы больше не в двадцать, а только в десять раз).
Слайд 18
исключение
В двадцатеричной системе счета древних майя есть исключение:
стоит прибавить к числу 359 только одну единицу первого
порядка, как это исключение немедленно вступает в силу.
Слайд 19
Исключение
Суть его сводится к следующему: 360 является
начальным числом третьего порядка (!) и его место уже
не на второй, а на третьей полке.
Слайд 20
принцип двадцатеричности нарушен!
начальное число третьего порядка больше
начального числа второго не в двадцать раз (20x20=400, а
не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен!Все верно. Это и есть исключение.