Презентация на тему Основные понятия. Описательная статистика

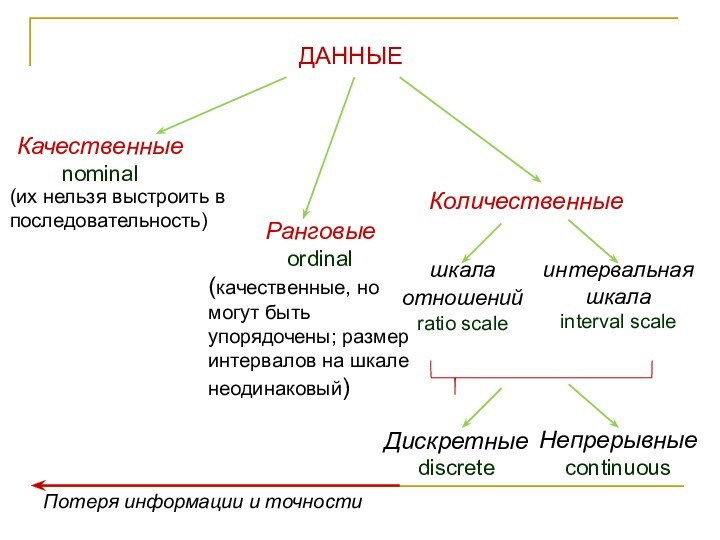
(переменных) – variable. Например:
вес, длина тела, пол, окрас,

Статистика – инструмент для количественного анализа и интерпретации данных

Статистический анализ данных

Описательная статистика
descriptive statistics

Индуктивная статистика
inferential statistics

на шкале неодинаковый)
Качественные
nominal
Дискретные
discrete
Непрерывные
continuous
шкала отношений ratio scale
интервальная шкала
interval scale

(их нельзя

Потеря информации и точности

шкалы одинаковый;
существует реальное нулевое значение.
Примеры: масса тела, размер выводка,

интервальная шкала (interval scale):
размер интервалов на протяжении всей шкалы одинаковый;
положение нулевой точки выбрано произвольно.
Примеры: температура по Цельсию, время дня, дата

– количество знаков показывает точность измерения (= ошибку измерения)
Если

рост, вес Ани, Тани и Мани

ОПИСЫВАЕМ ВЫБОРКУ
Индуктивная статистика : на основе свойств выборки

переменной и как его описывать
Что такое распределение ВЫБОРОЧНЫХ СРЕДНИХ

Необходимо для обдумывания и обсуждения данных

между значениями переменной и их вероятностями (на практике –

Можно представить в виде таблички или картинки.

ранговых переменных (bar graph). В русском языке обозначается словом

Оставим на некоторое время качественные и ранговые переменные и обратимся только к КОЛИЧЕСТВЕННЫМ

промежутки между столбиками

переменной (выстроим кроликов от меньшего к большему);
разобьём их на

интервалам, где высота столбика отражает ЧАСТОТУ
Частотное распределение переменной (frequency

Частота – то, сколько раз встретилось данное значение переменной

Интервалы должны быть:
одного размера,
не должны иметь общих точек,
для биологических данных – 10-20 интервалов

Полигон частот (frequency polygon)

быть воображаемой (гипотетической).

отражать свойства популяции.
Для этого она должна быть СЛУЧАЙНОЙ (random)

Пример: если в одну группу поместить зверьков, которые первыми вышли из клетки, а в другую – тех, кто в ней остался, выборки буду неслучайными

большинство распределений
«Середина» распределения;
«Ширина» распределения;
Форма распределения
Как описать частотное распределение

Речь идёт не только о количественных данных, но и о качественных

statistic
Все они могут служить оценками популяционного среднего.
Среднее в выборке

сумма всех значений переменной, делённая на количество значений
*«balancing point»

Среднее для выборки

Среднее для популяции

которое делит распределение пополам (его площадь в т.ч.): половина

1,0

1,5

4,1

5,7

9,5

6,0

7,1

7,9

10,4

11,0

Медиана

Имеет смысл не только для количественных переменных, но и для ранговых! (не для качественных).

3,2

центр распределения.
она содержит меньше информации, чем среднее (определяется

Распределение можно поделить не только на ДВЕ равные части, но и на:
четыре (значения, стоящие на границах - квартили);
восемь (... октили);
сто (... процентили);
N (... квантили).

Частотное распределение переменной (frequency distribution)

на четыре части так, что в каждой из них

переменной (frequency distribution)
«Середина» распределения
Существует не только для количественных, но

В первую очередь биолога интересует количество мод в распределении, а не мода как таковая

среднее СОВПАДАЮТ для симметричного унимодального распределения
К появлению перекоса чувствительнее

1/3

2/3

отклонение (standard deviation)
Дисперсия (variance)
* Это лишь основные параметры разброса
Размах

Хорош тем, что легко считается и имеет «биологический смысл».
Плох тем, что зависит лишь от 2-х точек из распределения. Недооценивает истинный размах в популяции. Если в статье приводится размах, следует привести ещё какую-нибудь характеристику разброса.

распределения
Для выборки:
Для популяции:
Поправка на то, что в выборке разброс

Стандартное отклонение зависит ото всех значений переменной.
Измеряется в тех же единицах, что и переменная!

популяции:
Равна стандартному отклонению в квадрате и содержит почти ту

распределения
Даёт понять, насколько на самом деле велик разброс в

diversity)
Показывают, насколько равномерно данные распределены по категориям. Разнообразие считается

Индекс Шеннона-Винера

p = доля объектов в той или иной категории;
k – число категорий.

Нормированный индекс Шеннона ( )

Этих индексов много для разных целей; это показатели ОПИСАТЕЛЬНОЙ статистики!

количеству «максимумов» (мод):
унимодальное
бимодальное
мультимодальное
обычно возникают, если популяция имеет естественные обособленные

(positively)
влево negatively
Как описать непрерывное распределение?

непрерывное распределение?

Унимодальное
Симметричное
Асимптотическое
Высота деревьев, масса тела новорожденных, IQ, скорость

Это непрерывное распределение

Название в честь Гаусса не совсем справедливо – первым его описал вовсе не он.
Симметрия и эксцесс.

от среднего значения до каждой из точек перегиба
Частотное распределение

Разброс распределения

график распределения, соответствует количеству измерений в выборке.
Отрезая часть распределения

частота

масса, кг

16% площади распределения ~ 16% объёма выборки

– значение переменной, левее которого находится 95% значений переменной
95%

– переменная, соответствующая количеству стандартных отклонений относительно среднего значения


выборка
популяция

определяется лишь 2-мя параметрами – μ и σ .
Необыкновенное

отклонений)
Откладывая от среднего значения стандартное отклонение (в ту или

Пример с IQ (μ=100, σ=15)

основные концепции в анализе данных:
Что такое РАСПРЕДЕЛЕНИЕ переменной и

выборка

популяция

раз центральный статистический вопрос: что мы можем сказать обо

На 1-м курсе института 25 групп по 22 студента.
Средняя масса студента – μ=50 кг, σ = 4 кг.
Посчитаем средние массы для каждой группы!

Форма распределений маленьких выборок не обязательна должна удовлетворять критериям нормального распределения.

…..

посчитали средние массы студентов в КАЖДОЙ группе, и теперь

50

5

55

60

45

40

50

1.2

Оно будет намного УЖЕ распределения всех студентов 1-го курса, и УЖЕ, чем каждое из распределений из отдельных групп

Это и будет распределение выборочных средних (sampling distribution of the means)

Пример про бутылки с кока-колой

выборочных средних
Выборка
(группа)
Популяция (1-й курс)
среднее
стандартное отклонение
>>

ПРЕДЕЛЬНАЯ ТЕОРЕМА
Определяет форму, среднее и разброс в распределении

Пример с монеткой

некоторая величина отклоняется от среднего под воздействием слабых, независимых

Пример про высоту деревьев в лесу

нас есть только одна выборка. Из неё мы получили

Мы знаем, что для нормального распределения есть z-оценка, значениям которой соответствуют определённые площади распределения.
Но мы также знаем, что выборочные средние образуют нормальное распределение!!
Это значит, что, зная среднее в популяции, мы можем предсказать (с … вероятностью) интервал, в который попадёт выборочное среднее.

Решим обратную задачу. Пусть нам известно μ, найдём

какая часть ОСОБЕЙ имеет массу больше 55 кг?
Другой вопрос:

изначально знаем среднюю массу студентов 1-го курса и стандартное

Зная стандартное отклонение в нем (=SE!!) можем рассчитать интервал, в который попадёт 95% (99%) всех средних масс в группах:

интервал (95% confidence interval): интервал значений переменной, который с

Т.е., расстояние от среднего значения в популяции до выборочного среднего для 95% выборок не больше 1.96 SE

Вернёмся к исходной задаче:
Как оценить среднюю массу в популяции, если нам известно среднее в выборке??

Расстояние от среднего в выборке до (неизвестного) среднего в популяции с вероятностью 95% не больше 1.96 SE

cv – critical value, критическое значение статистики (в данном случае, Z)

расположено μ?
Ответ: я точно не знаю, но наиболее вероятно

В примере нам было известно σ, но на практике оно обычно неизвестно!

знаем стандартное отклонение в популяции, и оцениваем его через

df

Пояснить про число степеней свободы

нормальному