- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
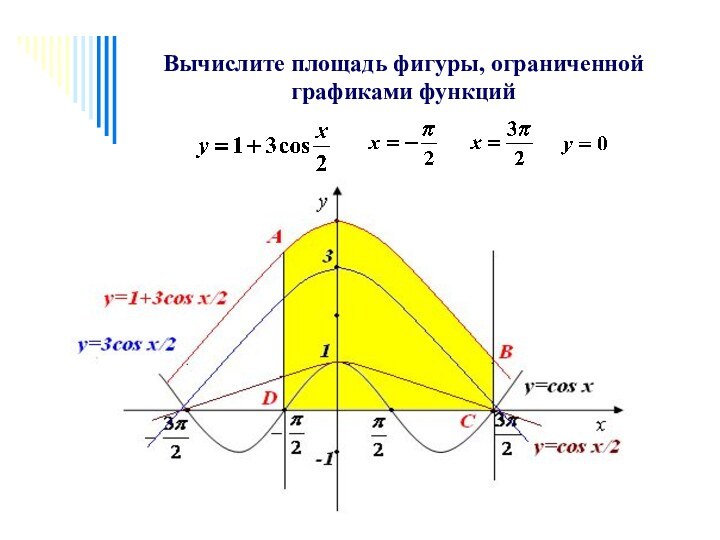
Презентация на тему Вычисление площадей плоских фигур с помощью определенного интеграла
Содержание
- 2. Вычислите площадь фигуры, ограниченной графиками функций
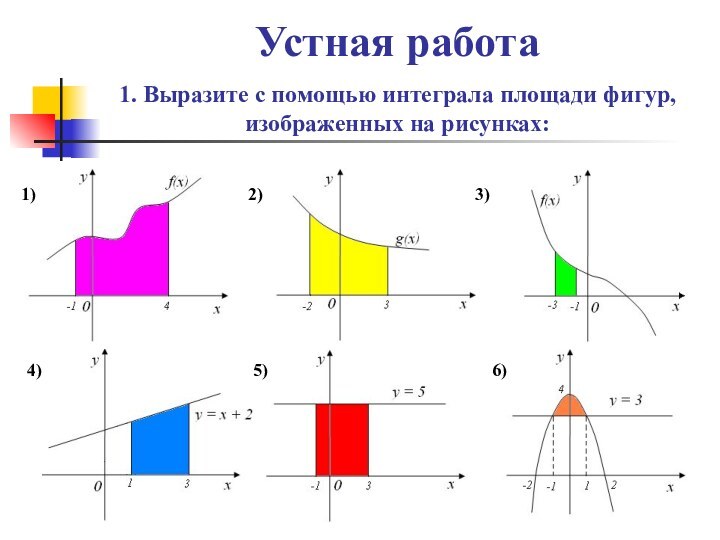
- 3. Устная работа 1. Выразите с помощью интеграла площади фигур, изображенных на рисунках:1)2)3)4)5)6)
- 4. 2. Вычислите интегралы:1).2).3).4).10,51641
- 5. Немного истории«Интеграл» придумал Якоб Бернулли (1690г.)«восстанавливать» от
- 6. Интеграл в древностиЭтот метод был подхвачен и
- 7. Исаак Ньютон (1643-1727) Наиболее полное изложение дифференциального
- 8. Лейбниц Готфрид Вильгельм (1646-1716) впервые использован Лейбницем
- 9. Определенный интегралИ. НьютонГ. Лейбницгде Формула Ньютона - Лейбница
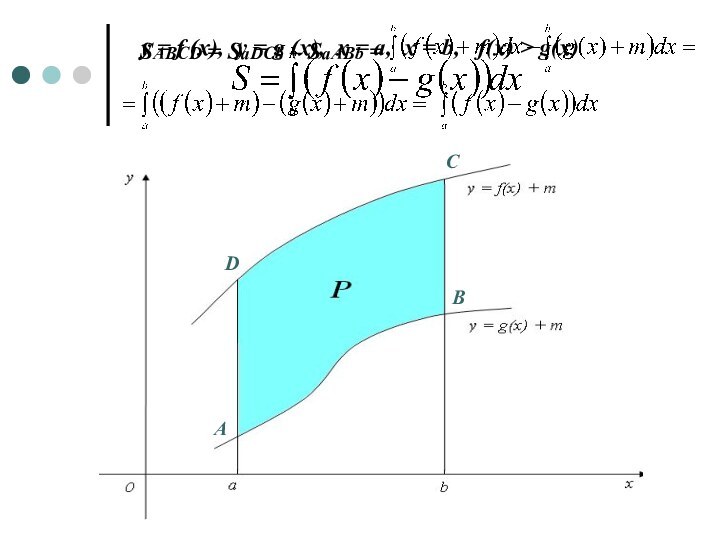
- 10. y = f (x), y = g
- 11. Пример. Вычислите площадь фигуры,
- 12. Задание1. Вычислите площадь фигуры,
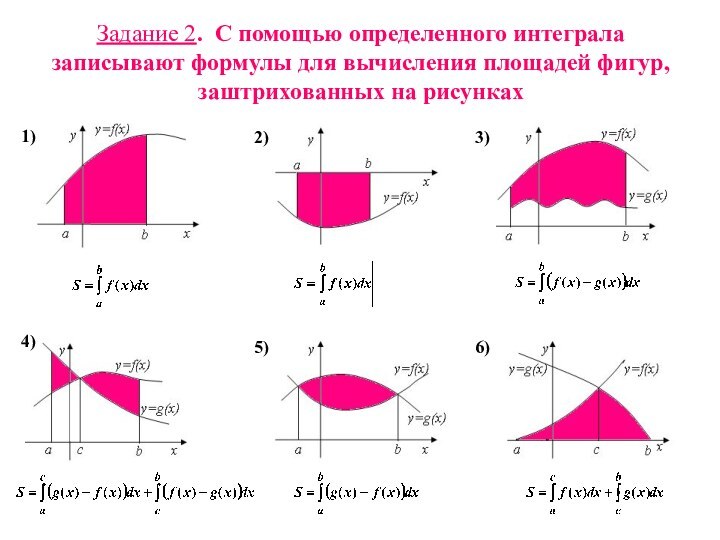
- 13. Задание 2. С помощью определенного интеграла записывают формулы для вычисления площадей фигур, заштрихованных на рисунках1)2)3)4)5)6)
- 14. Подберите из данных формул для вычисления площади
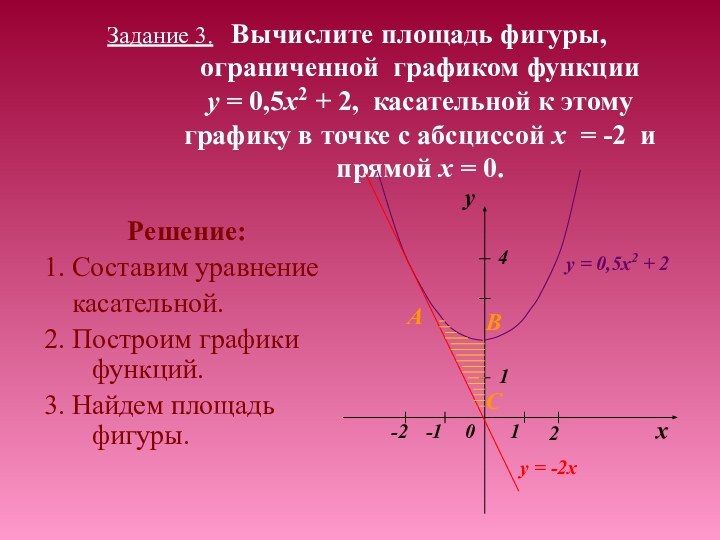
- 15. Задание 3. Вычислите площадь фигуры,
- 16. Итоги урока
- 17. Скачать презентацию
- 18. Похожие презентации












Слайд 5
Немного истории
«Интеграл» придумал Якоб Бернулли (1690г.)
«восстанавливать» от латинского
integro
«целый» от латинского integer
от латинского
primitivus – начальный,
ввел
Жозеф Луи Лагранж
(1797г.)
«Примитивная функция»,
Слайд 6
Интеграл в древности
Этот метод был подхвачен и развит
Архимедом, и использовался для расчёта площадей парабол и приближенного
расчёта площади круга.Евдокс Книдский
Архимед
Первым известным методом для расчёта интегралов является метод исчерпания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен.
Слайд 7
Исаак Ньютон
(1643-1727)
Наиболее полное изложение дифференциального и интегрального исчислений
содержится в
«Методе флюксий...»
(1670–1671, опубликовано в 1736).
Переменные
величины - флюенты(первообразная или неопределенный интеграл)Скорость изменения флюент – флюксии (производная)
Слайд 8
Лейбниц Готфрид Вильгельм
(1646-1716)
впервые использован Лейбницем в конце
XVII века
Символ образовался из буквы
S — сокращения слова
summa
(сумма) Слайд 11 Пример. Вычислите площадь фигуры,
ограниченной линиями
y = x, y = 5 – x, x = 1, x = 2.x
y
0
1
2
5
5
y = x
y = 5 - x
A
B
C
D
Слайд 12 Задание1. Вычислите площадь фигуры,
ограниченной линиями
y
= 3 – x2,y = 1+ | x |
y = 1 + |x|
y
х
0
1
1
-1
3
y = 3 – х2
S1
S2
S = S1 + S2
Слайд 13 Задание 2. С помощью определенного интеграла записывают формулы
для вычисления площадей фигур, заштрихованных на рисунках
1)
2)
3)
4)
5)
6)
Слайд 14 Подберите из данных формул для вычисления площади фигуры
ту, которая подходит к одному из шести чертежей.
S1 =
S2 =
S3 =
S4 =
S5 =
S6 =
5
1
2
3
4
6
Слайд 15 Задание 3. Вычислите площадь фигуры,
ограниченной графиком
функции y = 0,5x2 + 2, касательной к этому графику в точке с абсциссой х = -2 и прямой х = 0.Решение:
1. Составим уравнение
касательной.
2. Построим графики функций.
3. Найдем площадь фигуры.
х
y
0
-1
1
-2
1
4
у = -2х
у = 0,5х2 + 2
А
B
C
2





























