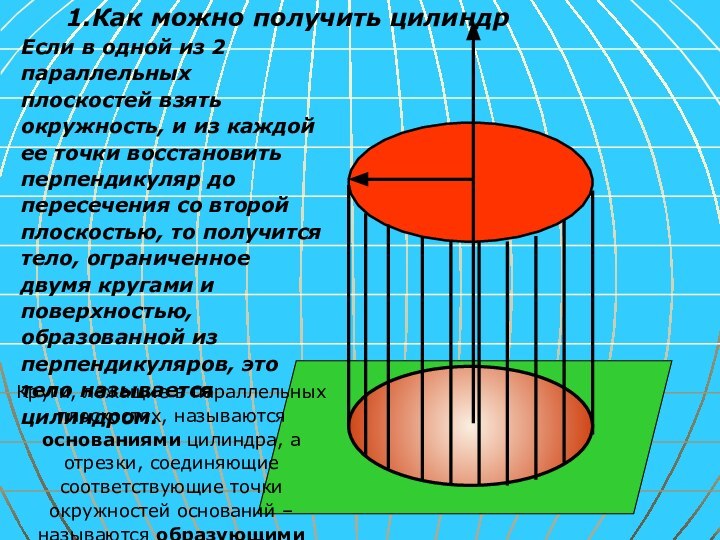
окружность, и из каждой ее точки восстановить перпендикуляр до
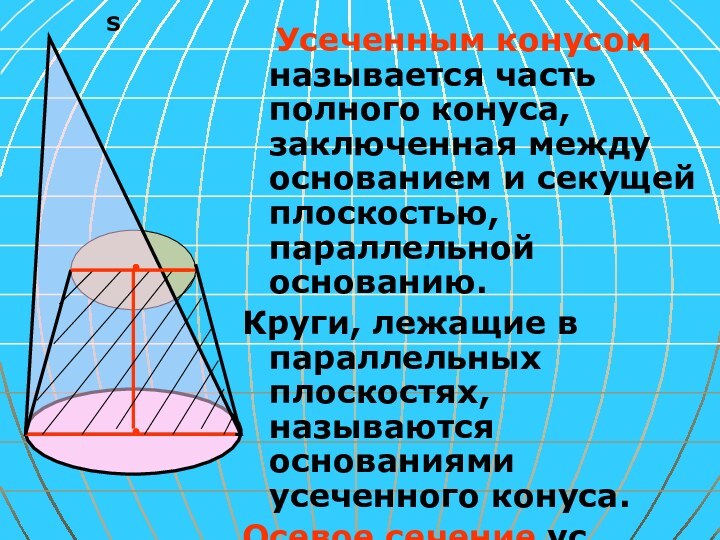
пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром.1.Как можно получить цилиндр
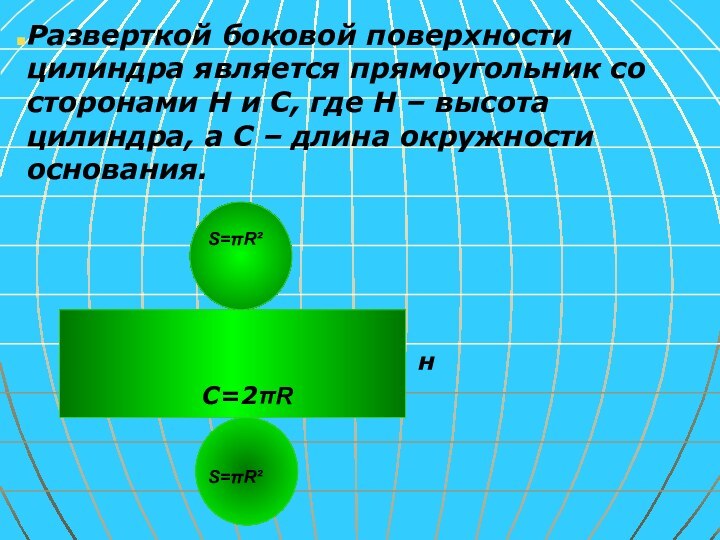
Круги, лежащие в параллельных плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей оснований –называются образующими цилиндра.