+ y2 = R2
Уравнение окружности с центром в точке
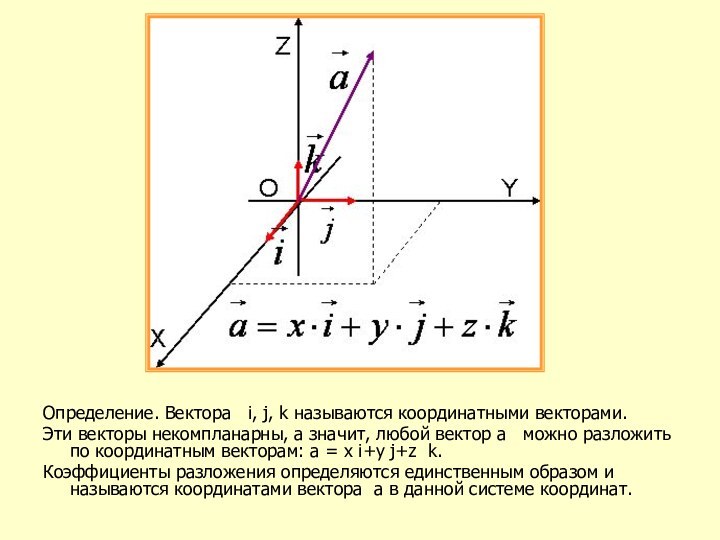
(x0;y0) : (x - x0)2 + (y - y0)2 = R2Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.
Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.
Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).
Уравнение окружности.