Слайд 2
Примеры моделей
Оптимизационные модели
Математическая оптимизационная модель должна содержать следующие
основные компоненты:
Переменные – значения, которых необходимо вычислить.
Целевая функция –
цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти ее максимум или минимум.
Ограничения – записанные, математически ограничения, выявленные из анализа предметной ситуации.
Слайд 3
Примеры моделей
Оптимизационные модели
Задача распределения ресурсов
На предприятии, выпускающем неоднородную
продукцию, руководители хотят определить уровни производства этой продукции на
некоторый период времени.
Исходные данные:
количество материалов (X, Y, Z), требуемых на каждом этапе технологического процесса для выпуска единицы продукции;
объем запасов этих материалов на складе;
доход, получаемый в результате выпуска единицы продукции.
Цель планирования – увеличение прибыли.
Слайд 4
Примеры моделей
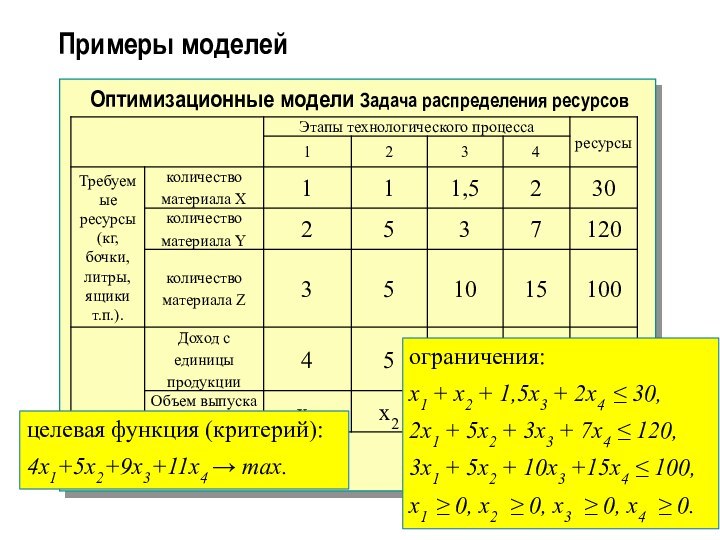
Оптимизационные модели Задача распределения ресурсов
целевая функция (критерий):
4x1+5x2+9x3+11x4
→ max.
ограничения:
x1 + x2 + 1,5x3 + 2x4 30,
2x1 + 5x2 + 3x3 + 7x4 120,
3x1 + 5x2 + 10x3 +15x4 100,
x1 0, x2
0, x3 0, x4 0.
Слайд 5
Описательные (дескриптивные) модели
Основная задача: описание процесса с помощью
математического аппарата в целях изучения поведения систем и прогнозирования
их дальнейшего развития.
Виды моделей:
Регрессионные модели
Модели кластеризации
Модели ассоциации
Области применения:
в практике маркетинговых исследований
интеллектуальный анализ данных
отражение содержания и основных свойств экономических объектов
Слайд 6
Основные подходы к моделированию
Использование законов природы
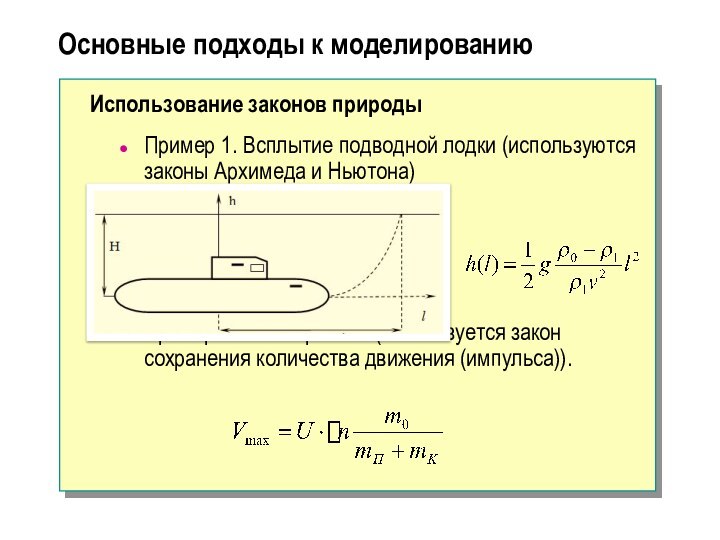
Пример 1. Всплытие подводной
лодки (используются законы Архимеда и Ньютона)
Пример 2. Полет ракеты
(используется закон сохранения количества движения (импульса)).
Слайд 7
Основные подходы к моделированию
Принцип аналогии
Применение аналогий основано на
свойстве моделей:
универсальности, т.е. применимости к объектам принципиально различной природы.
Системы
можно представить как совокупность простых элементов типа:
резистора, оказывающего сопротивление переносу субстанции,
конденсатора, обладающего свойством инерционности, что проявляется в стремлении сохранить поток субстанции неизменным.
Слайд 8
Основные подходы к моделированию
Использование типовых моделей
В качестве детерминированных
моделей:
дифференциальные и интегральные уравнения
конечные автоматы
сетевые модели
В качестве
стохастических моделей:
вероятностные автоматы
системы массового обслуживания
игровые модели
Слайд 9
Иерархический подход к получению моделей
Процесс построения моделей
Словесное описание
объекта или явления, т.е. сформировываются предметная модель и цели
исследования модели
Выбирается или формулируется закон, которому подчиняется объект. Модель записывается в математической форме.
Завершается построение модели. Проводится селекция факторов, при которой отбрасываются несущественные и малозначимые факторы.
Построенная модель исследуется и делается вывод о ее адекватности, т.е. соответствии объекту и целям исследования.
Слайд 10
Конечные автоматы
Автомат можно рассматривать как некоторое устройство (черный
ящик), на которое подаются входные сигналы, снимаются выходные и
которое может иметь некоторые внутренние состояния.
Состояние – это то, на что влияет управление, и что вместе с управлением определяет результат (выход).
Конечным автоматом называется автомат, у которого множество внутренних состояний, входных и выходных сигналов являются конечными множествами.
Работа конечного автомата описывается двумя функциями:
- функция переходов
- функция выхода
x – переменная состояния; u – переменная управления;
y – переменная выхода; t – момент времени (t = 0,1,2,3…).
Слайд 11
Конечные автоматы
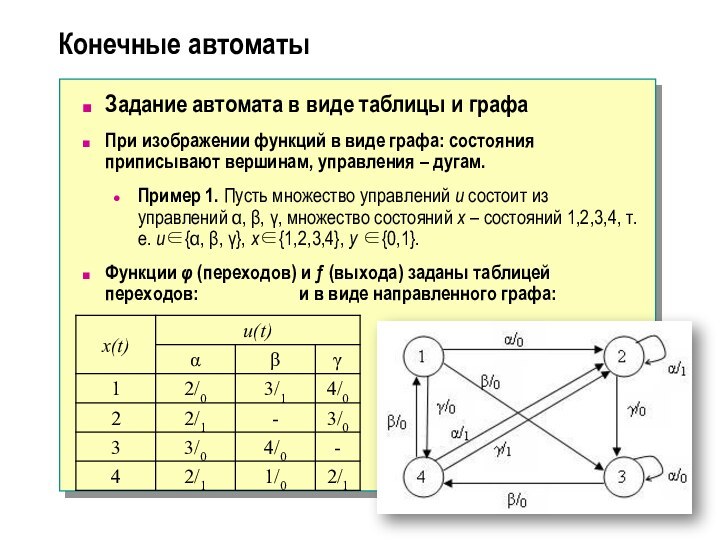
Задание автомата в виде таблицы и графа
При
изображении функций в виде графа: состояния приписывают вершинам, управления
– дугам.
Пример 1. Пусть множество управлений u состоит из управлений α, β, γ, множество состояний x – состояний 1,2,3,4, т.е. uα, β, , x1,2,3,4, y 0,1.
Функции φ (переходов) и (выхода) заданы таблицей переходов: и в виде направленного графа:
Слайд 12
Конечные автоматы
Задание автомата в виде таблицы и графа
Пример
2. Рассмотрим автомат, который выдает билет при опускании в
него монет в сумме 3 руб., причем он принимает монеты 50 коп., 1рубль и 2 рубля. Автомат может давать сдачу. Требуется составить функцию перехода и выхода.
uα=0,5, β=1, =2, x1,2,3,4,5,6, y 10,1. , y 20, 0.5, 1, 1.5
Функция переходов Функция выхода
Слайд 13
Конечные автоматы
Матричное задание автомата
Матрица переходов – квадратная матрица,
размерность которой совпадает с числом состояний, а элементами являются
дуги, соединяющие состояния
Слайд 14
Минимизация конечных автоматов
Минимизация автоматов – сокращение числа состояний
путем объединения эквивалентных состояний.
Состояния называются эквивалентными, если поведение автомата
одинаково независимо от того, какое из них является исходным.
Состояние называется k‑эквивалентным, если автомат, находясь в любом из них, имеет одинаковое поведение в течение k тактов.
k‑эквивалентные состояния образуют k-эквивалентные классы.
Слайд 15
Определение эквивалентных состояний автомата
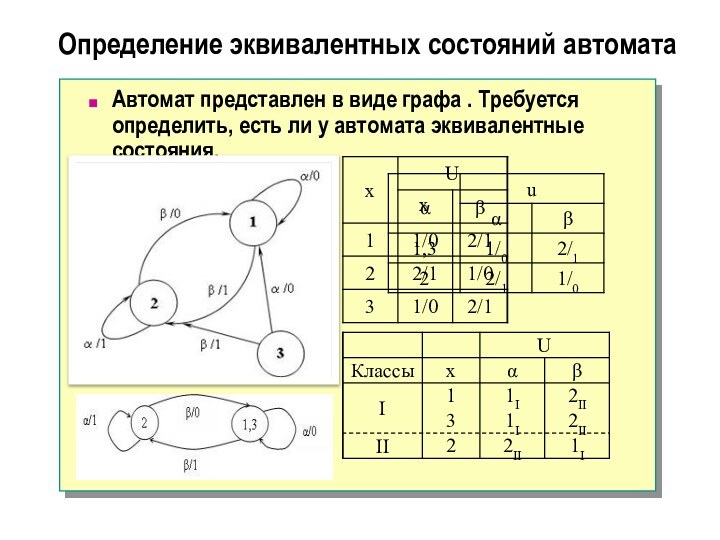
Автомат представлен в виде графа
. Требуется определить, есть ли у автомата эквивалентные состояния.
Слайд 16
Аналитическое задание конечных автоматов
Достоинства аналитического представления конечных автоматов:
компактность
записи по сравнению с табличным, графовым или матричным заданиями;
простота
моделирования работы конечных автоматов на ЭВМ;
аналитическое представление необходимо при синтезе структуры автомата, так как при таком задании функции функциональных преобразователей выражаются через элементарные функции, реализуемыми простыми элементами.
Для формального описания цифровых управляющих устройств применяется аппарат алгебры логики.
Слайд 17
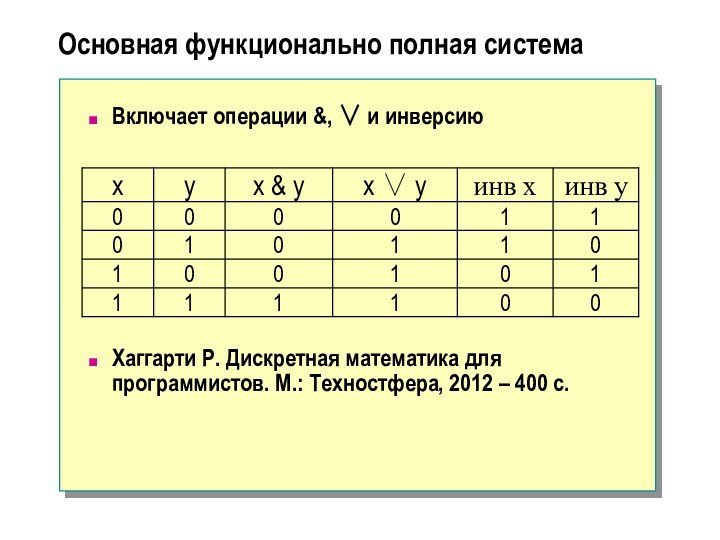
Основная функционально полная система
Включает операции &, и
инверсию
Хаггарти Р. Дискретная математика для программистов. М.: Техностфера, 2012
– 400 с.
Слайд 18
Нормальные формы
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного
числа различных членов, каждый из которых представляет собой конъюнкцию
отдельных переменных или их отрицаний, входящих в данный набор не более одного раза
Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа различных членов, каждый из которых представляет собой дизъюнкцию отдельных переменных или их отрицаний, входящих в данный набор не более одного раза
СДНФ – СКНФ –
Слайд 19
Разложение функций на конституенты
Конституентой единицы называют конъюнкцию,
содержащую все переменные или их инверсии, которая обращается в
единицу только при одном выборочном наборе переменных.
Конституентой нуля называют дизъюнкцию, содержащую все переменные или их инверсии, которая обращается в нуль только при одном выборочном наборе переменных.
Слайд 20
Переход от табличного задания функции к аналитическому
Табличное представление
функции
Функция в виде СДНФ:
Функция в виде СКНФ:
Слайд 21
Вероятностные автоматы
Вероятностные (стохастические) автоматы представляют собой конечные автоматы
со случайными управлениями, у которых, как правило, учитываются только
состояния.
Пример:
модель системы, которая случайным образом может оказаться в одном из технических состояний:
исправное, неисправное, поиск неисправности, ремонт и т.д.
Слайд 22
Марковские цепи с дискретным временем
Марковским называется случайный процесс,
состояние которого в очередной момент времени t + ∆t зависит только от
текущего состояния в момент времени t.
Исходные данные для определения дискретной марковской цепи:
множество состояний
матрица вероятностей переходов
вектор начальных вероятностей
Слайд 23
Марковские цепи с дискретным временем
Марковская цепь изображается в
виде графа, вершины которого соответствуют состояниям цепи и дуги
– переходам между состояниями
Пример. Дана матрица вероятностей переходов
Граф:
вектор начальных вероятностей
Слайд 24
Анализ марковских цепей
Результат анализа марковской цепи:
как при известном
начальном состоянии от шага к шагу меняются вероятности состояний,
в которых может находиться система,
каковы установившиеся значения этих вероятностей.
Для расчета вероятностей используется уравнение Колмогорова-Чепмена
вероятности состояний вычисляются рекуррентно:
При n→∞ определяют установившиеся (финальные) вероятности
Слайд 25
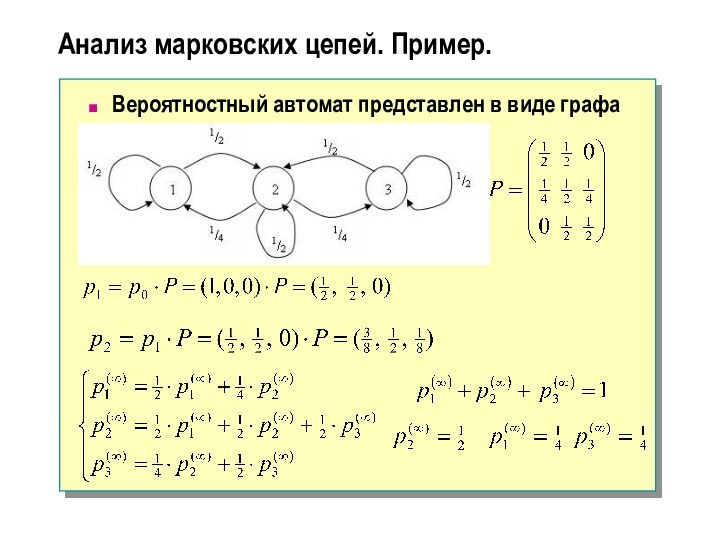
Анализ марковских цепей. Пример.
Вероятностный автомат представлен в виде
графа
Слайд 26
Марковские процессы
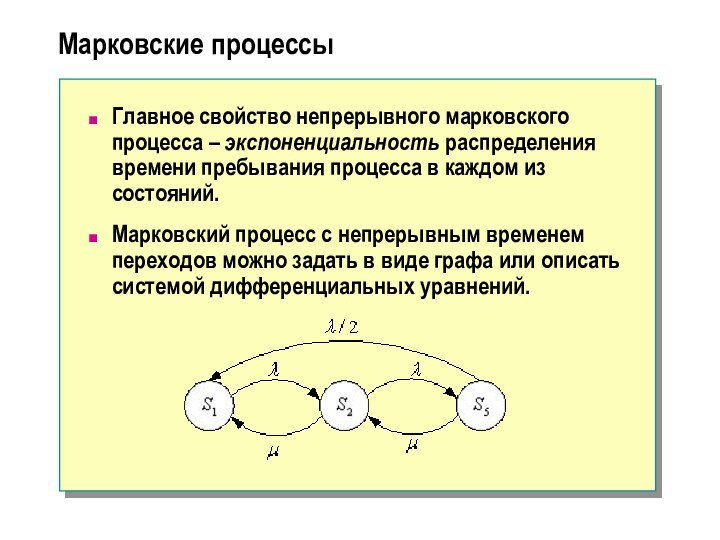
Главное свойство непрерывного марковского процесса –
экспоненциальность распределения времени пребывания процесса в каждом из состояний.
Марковский процесс с непрерывным временем переходов можно задать в виде графа или описать системой дифференциальных уравнений.
Слайд 27
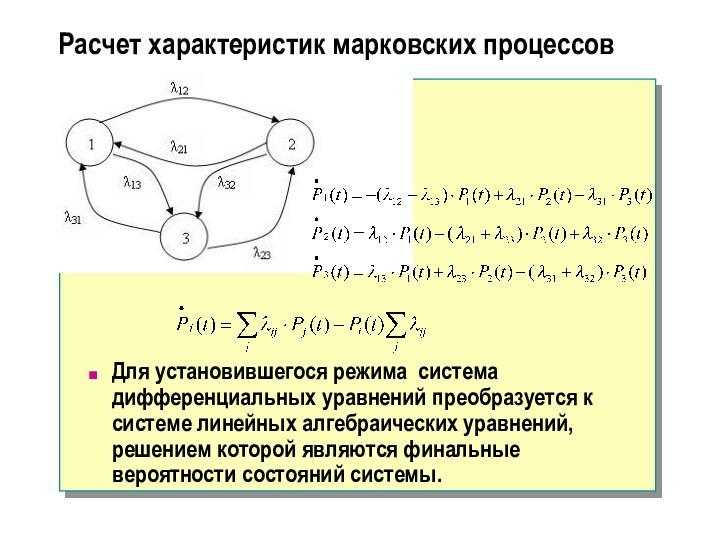
Расчет характеристик марковских процессов
Для установившегося режима система дифференциальных
уравнений преобразуется к системе линейных алгебраических уравнений, решением которой
являются финальные вероятности состояний системы.