связей
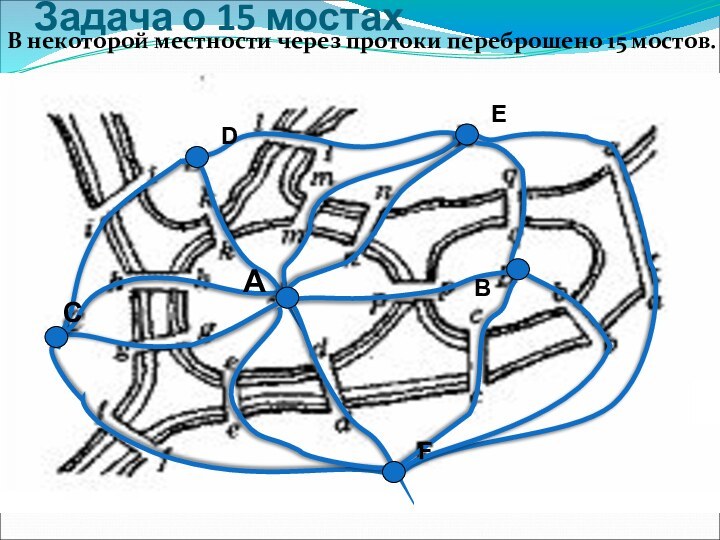
Сеть
Граф с возможностью множества различных путей перемещения по ребрам
между некоторыми парами вершинГраф называется связным
если любая пара его вершин — связная.
Ребро соединяет две вершины графа
элемент (точка) графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом
Вершина
Ребро
это ориентированное ребро.
Дуга
ребро, начало и конец которого находятся в одной и той же вершине
Петля
любой связный граф, не имеющий циклов.
Дерево