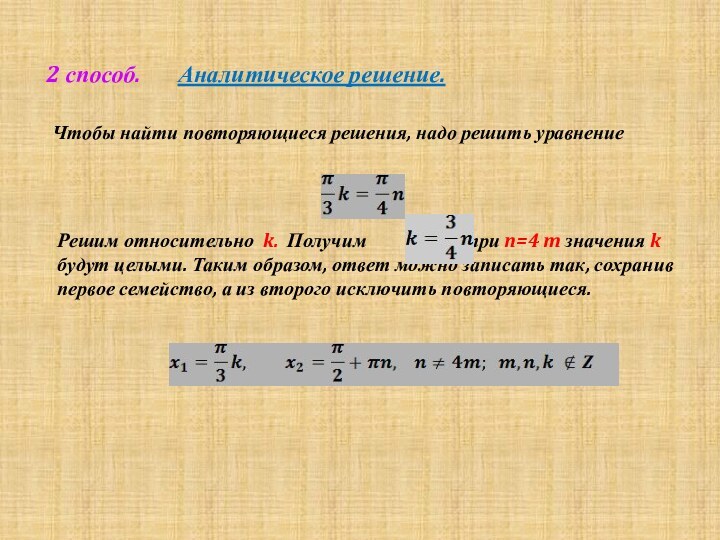
метод нахождения подходящих корней заключатся в решении диофантовых
уравнений с целыми коэффициентами для этого необходимо:- найти наибольший общий делитель коэффициентов при неизвестных ;
попробовать сократить на него обе части уравнения (разумеется, свободный член должен при этом остаться целым числом).
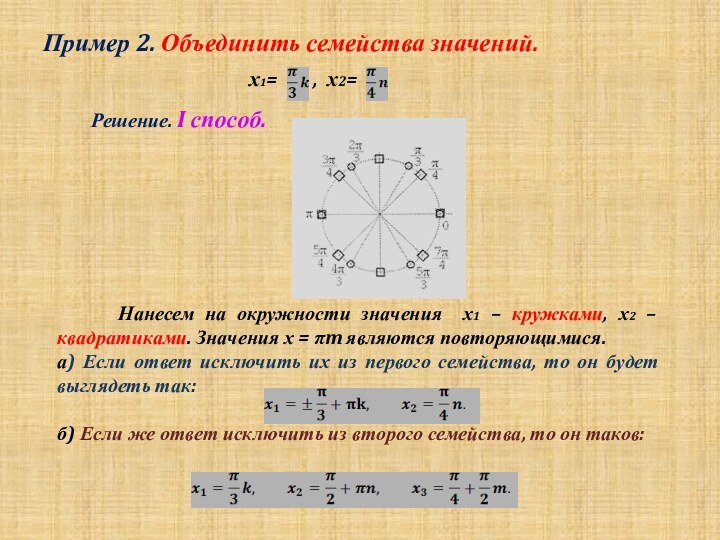
Второй метод заключается в изображении всех решений на тригонометрической окружности и исключении неподходящих решений.
Метод этот очень прост в применении, если решения легко изобразить на тригонометрической окружности.
Решая тригонометрические уравнения , возникает вопрос отбора корней ,связанных с областью определения и другими условиями.
Рассмотрим пример : 21k - 24n = 8 и решим его первым способом.
Набольший общий делитель коэффициентов равен 3, и сократить его не удается, так как 8 на 3 не делится. Тогда можно сразу сказать, что это уравнение решений в целых числах не имеет.