- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Несобственный интеграл
Содержание
- 2. определение несобственного интеграланесобственный интеграл по неограниченному промежуткупримернесобственный интеграл от неограниченной функциипример Содержание
- 3. Определение несобственного интегралаИнтеграл называется несобственным, если:Один или
- 4. Несобственный интеграл первого родаПусть функция f(x) определена
- 5. ПримерВычислить несобственный интеграл:Несобственный интеграл расходится, и площадь закрашенной криволинейной трапеции равна бесконечности
- 6. ПримерВычислить несобственный интеграл:Площадь закрашенной бесконечной криволинейной трапеции равна конечному числу, то есть несобственный интеграл сходится
- 7. Несобственный интеграл второго родаПусть функция f(x) непрерывна
- 8. ПримерДобавка +0 означает, что мы стремимся к
- 9. ПримерВычислим:Если подынтегральная функция не существует в точке
- 10. Скачать презентацию
- 11. Похожие презентации
определение несобственного интеграланесобственный интеграл по неограниченному промежуткупримернесобственный интеграл от неограниченной функциипример Содержание








Слайд 2
определение несобственного интеграла
несобственный интеграл по неограниченному промежутку
пример
несобственный
интеграл от неограниченной функции
Слайд 3
Определение несобственного интеграла
Интеграл называется несобственным, если:
Один или оба
его предела бесконечны
Подынтегральная функция имеет точки разрыва
И
то, и другое вместе
Слайд 4
Несобственный интеграл первого рода
Пусть функция f(x) определена на
промежутке [a,∞)
и интегрируема на любом отрезке:- формула Ньютона-Лейбница
Формула Ньютона-Лейбница для несобственного интеграла
Если предел конечен, то несобственный интеграл называется сходящимся, иначе - расходящимся
Слайд 5
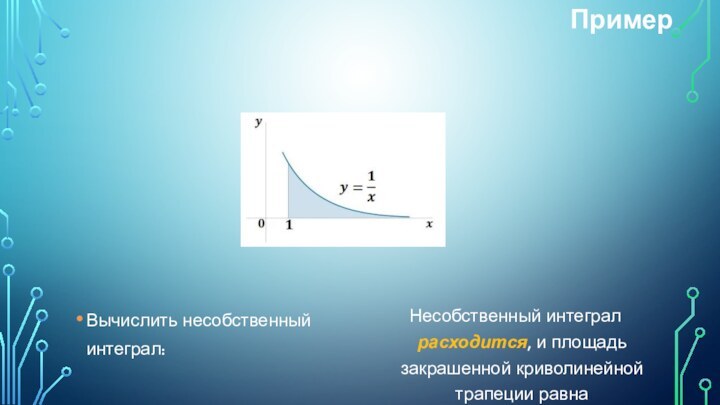
Пример
Вычислить несобственный интеграл:
Несобственный интеграл расходится, и площадь закрашенной
криволинейной трапеции равна бесконечности
Слайд 6
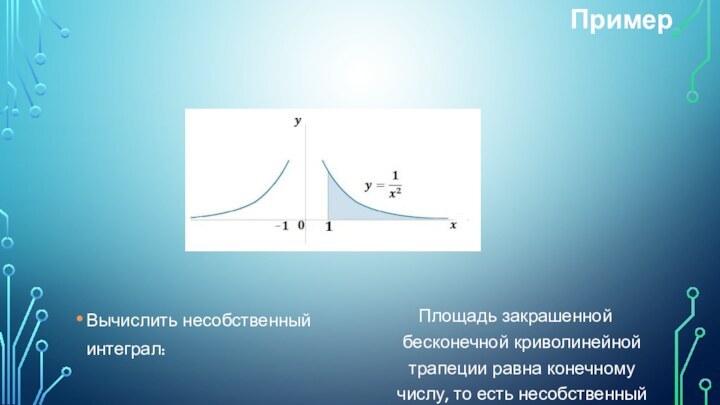
Пример
Вычислить несобственный интеграл:
Площадь закрашенной бесконечной криволинейной трапеции равна
конечному числу, то есть несобственный интеграл сходится
Слайд 7
Несобственный интеграл второго рода
Пусть функция f(x) непрерывна на
промежутке [a,b) и
интегрируема на любом отрезке: В отличие от определенного интеграла, в несобственном интеграле подынтегральная функция f(x) не существует в одном из следующих случаев:
в точке x = a
в точке x = b
в обеих точках сразу
на отрезке интегрирования
Слайд 8
Пример
Добавка +0 означает, что мы стремимся к значению
½ справа
Знак минус указывает на то, что трапеция расположена
под осью OxНайдём неопределенный интеграл:
Вычислим несобственный интеграл:
Если подынтегральная функция не существует в точке x=a:





























