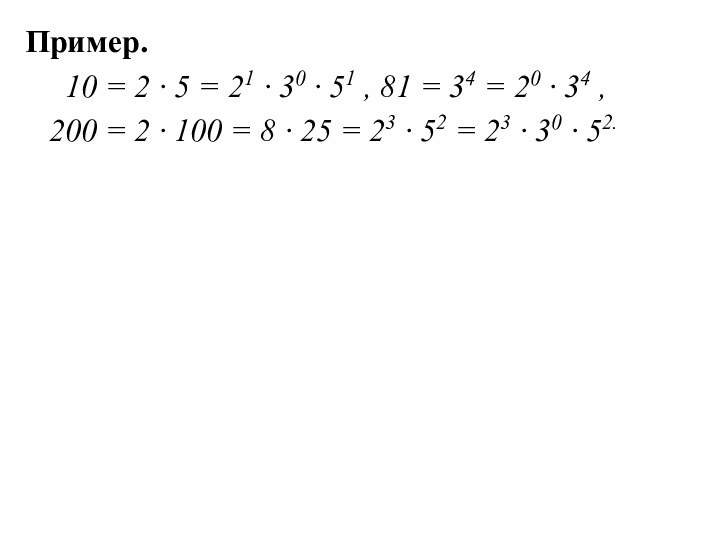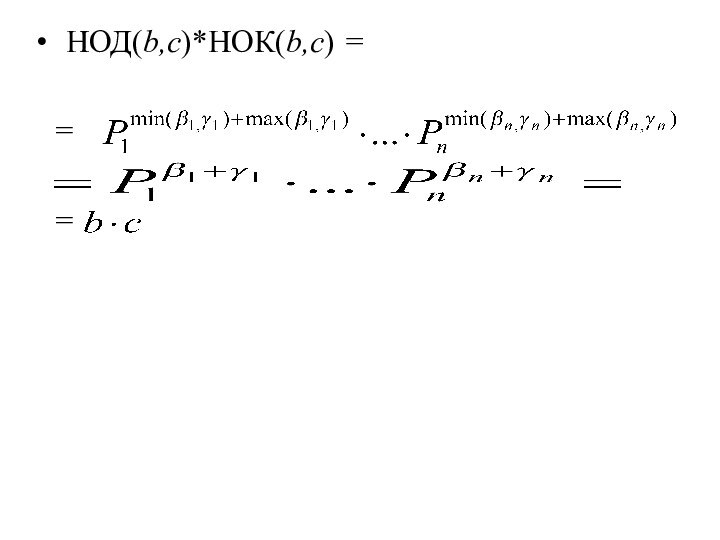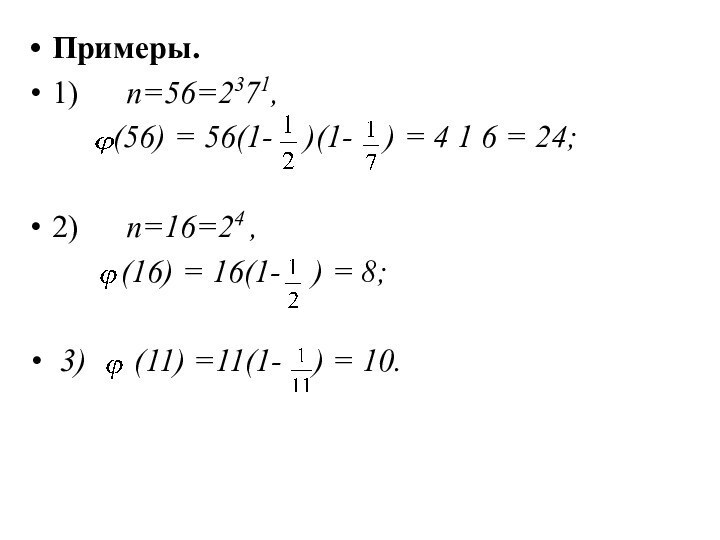Слайд 2
Примеры. Числа 2, 3, 5, 7, 11 простые,
числа 4, 6, 18, 100 составные. Отметим, что число
1 не является ни простым, ни составным.
Существует стандартная система обозначений простых чисел: Р1 – первое по величине простое число (ясно, что Р1 = 2),
Р2 – следующее простое число,
(Р2 = 3), (Р3 = 5), (Р4 = 7), (Р5 = 11), (Р6 = 13), (Р7 = 17), (Р8 = 19) и т.д.
Вообще Рn – n-ое простое число.
К сожалению, не существует аналитической формулы f (n), которая позволила бы вычислять любое простое число Pn.
Слайд 3
Теорема 2. Простых чисел существует бесконечно много.
Доказательство.
Допустим, существует лишь конечное число простых чисел. Перечислим их:
P1, Р2, …, РN.
Значит, любое другое натуральное число содержит в качестве делителя по крайней мере одно из
Рi (i = 1, 2, …, N).
Рассмотрим число
Р = Р1 Р2 … РN + 1.
Очевидно, что это число не делится ни на одно из чисел
Слайд 4
так как при делении на любое из этих
чисел Р дает в остатке 1.
Значит, допущение о
конечности множества простых чисел неверно. Простых чисел существует бесконечно много.
Замечание. По дошедшим до нас историческим источникам это доказательство принадлежит Евклиду и является первым примером в математике доказательства «методом от противного».
Простые числа являются «кирпичиками» из которых строятся все остальные натуральные и целые числа, отличные от 0, -1, 1.
Слайд 5
Теорема3. (основная теорема арифметики). Для любого натурального числа
а ≠ 1 имеет место равенство
а =
для некоторых неотрицательных целых
α1, α2, …, αк и натурального k.
Правая часть равенства называется разложением числа а в произведение простых чисел. Такое разложение при фиксированной нумерации множества простых чисел единственно.
Слайд 6
Пример.
10 = 2 ∙
5 = 21 ∙ 30 ∙ 51 , 81
= 34 = 20 ∙ 34 ,
200 = 2 ∙ 100 = 8 ∙ 25 = 23 ∙ 52 = 23 ∙ 30 ∙ 52.
Слайд 7
Определение 4. Пусть а,b N. Число с называется
общим делителем а и b , если оба они
делятся на с без остатка.
Примеры. Пусть а = 24, b = 36.
Тогда общими делителями a и b будут числа 1, 2, 3, 4, 6 и 12.
Число 8 не будет общим делителем чисел 24 и 36.
Пусть а = 10, b = 30.
Общие делители – 1, 2, 5.
Пусть а = 16, b = 35.
Общий делитель, равный 1, единственный.
Слайд 8
Теорема 5. Пусть
и
Число b является делителем а в
том и только в том случае, когда
βi ≤ αi для любого i = 1,…, n.
Слайд 9
Следствие 6.
Пусть для натурального числа а имеет место
равенство
Тогда число делителей а вычисляется
по формуле (α1 + 1) ∙ (α2 + 1) ∙ … ∙ (αn + 1).
Слайд 10
Теорема 7. Пусть
и
Тогда число
является
общим делителем чисел а и b в том и
только в том случае, когда
γ1 ≤ min (α1, β1), γ2 ≤ min (α2, β2), …, γn ≤ min (αn, βn).
Слайд 11
Определение 8.
Число c называется наибольшим
общим делителем чисел а и b
(обозначение: с
= НОД (а, b)),
если с является самым большим из всех общих делителей чисел а и b.
Примеры. Пусть а = 24, b = 30.
Тогда НОД (24, 30) = 6.
Если а = 10, b = 33, то НОД (10, 33) = 1;
НОД (а, а) = а.
Пусть а = 12, b = 48.
Тогда НОД (12, 48) = 12.
Слайд 12
Теорема 9. Пусть а и b натуральные числа,
Тогда НОД (а,b)=
где γi = min (αi,βi),
i = 1,2,3, …, n.
Слайд 13
Следствие 10.
Любой общий делитель чисел а и
b является также делителем НОД (а, b).
Определение 11.
Число
а называется кратным числу b (а,b N), если а делится на b или, что тоже самое, b есть делитель а.
Тот факт, что а делится на b, будет обозначать как b .
Слайд 14
Пример. Пусть b =3.
Тогда кратным ему будут
числа 3,6, 9, 12, … . Их можно описать
общей формулой
а = 3n (n N).
Этот пример показывает, что в отличие от делителей, количество кратных любому натуральному числу b бесконечно.
Слайд 15
Определение 12.
Если число а делится на число
b и с, то а называется общим кратным
чисел b и с.
Примеры.
Если b = 6, c = 8, то общее кратное этих чисел равно 24.
Также общими кратными являются числа
48, 72, … .
Слайд 16
Теорема 13. Пусть,
Тогда число
является общим кратным чисел
b и с тогда и только тогда, когда
α1
≥ max (β1,γ1), α2 ≥ max (β2,γ2), …, αn ≥ max (βn,γn).
Слайд 17
Доказательство.
Пусть а – общее кратное
b и с.
Так как а делится на
b, то
αi ≥ βi, i = 1, 2, 3, …, n.
Так как а делится на с, то
αi ≥ γi, i = 1, 2, 3, …, n.
Так как αi ≥ βi и αi ≥ γi , то αi ≥ max (βi,γi). Докажем в другую сторону.
Так как αi ≥ max (βi,γi), то αi ≥ βi
для каждого i = 1, 2, 3, …, n,
значит а делится на b.
Аналогично, а делится на с, то есть
а – общее кратное b и с.
Слайд 18
Определение 14.
Самое маленькое из всех общих кратных
натуральных чисел b и с называется наименьшим общим кратным
b и с и обозначается НОК (b, c).
Примеры.
НОК (3, 5) = 15, НОК (4, 6) = 12,
НОК (36, 64) = 576, НОК (2, 8) = 8,
НОК (а, а) = а, НОК (1, а) = а.
Слайд 19
Теорема 15. Пусть
Число
является НОК (b, с)
в том и только в том
случае, когда
αi = max (βi,γi), i = 1, 2, 3, …, n
Слайд 20
Следствие 16.
Любое общее кратное чисел b и
с делится на НОК(b, с).
Лемма 17. Для
любых чисел х, у
max (x, y) + min (x, y) = x + y.
Слайд 21
Доказательство. Рассмотрим три случая:
1) х = у, тогда
max (x, y) = x, min (x, y) =
x, поэтому
max (x, y) + min (x, y) = 2 x и х + у = 2х ;
2) х > у, тогда
max (x, y) = x, min (x, y) = y,
следовательно
max (x, y) + min (x, y) = x + y ;
3) x < y, тогда
max (x, y) = y, min (x, y) = x,
поэтому max (x, y)+ min (x, y) = y + x = x + y.
Слайд 22
Теорема 18.
Для любых натуральных чисел b и
с
НОД (b, с) · НОК (b, с) =
b · c.
Доказательство. Пусть
и
Тогда
Слайд 24
Определение 19. Числа а и b называются взаимно
простыми, если НОД (а, b) = 1. Другими словами,
если а и b не имеют общих делителей, отличных от 1.
Примеры.
3, 8 – взаимно просты,
1, 5 взаимно просты,
4, 6 – не взаимно просты.
Слайд 25
Определение 20.
Функцией Эйлера φ (n) называется количество
чисел меньших, либо равных n, которые взаимно просты с
n.
Примеры.
1) φ (12) = 4.
Перечислим все числа ≤ 12 и взаимно простые с 12: 1,5, 7, 11;
2) φ(36) = 12.
Перечислим все необходимые числа: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35;
3) φ(7) = 6.
Слайд 26
Теорема 21.
Пусть
n =
,
причем αi > 0 и ki kj (i j),
i ,j= 1, 2, …, n. Тогда