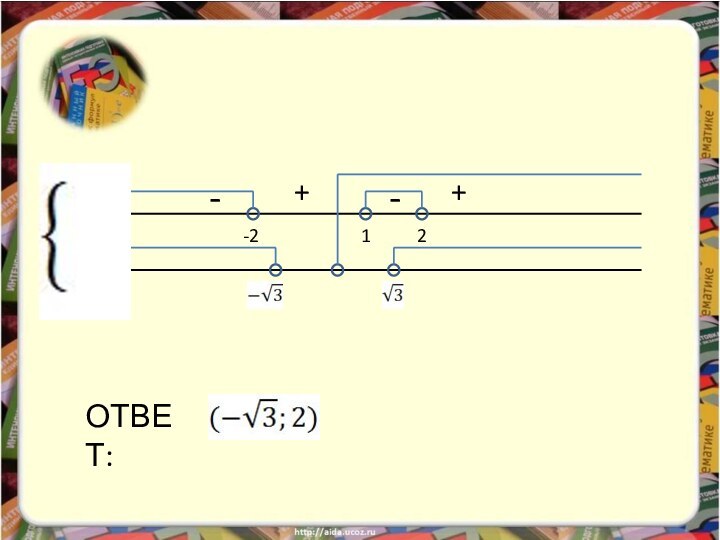
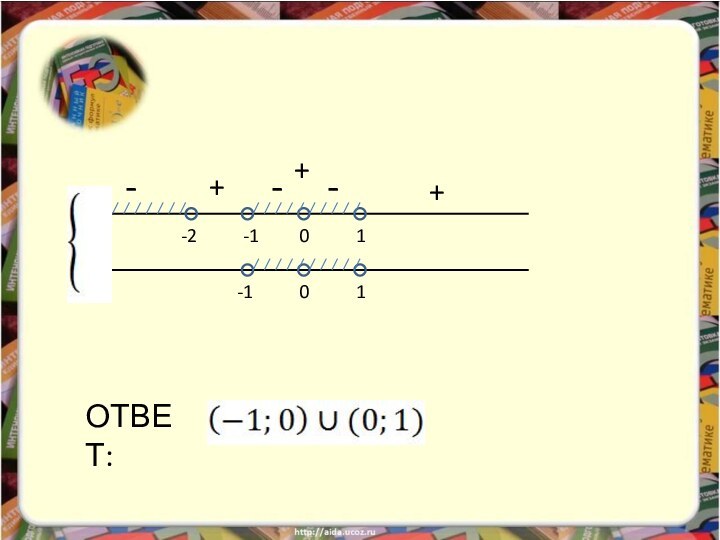
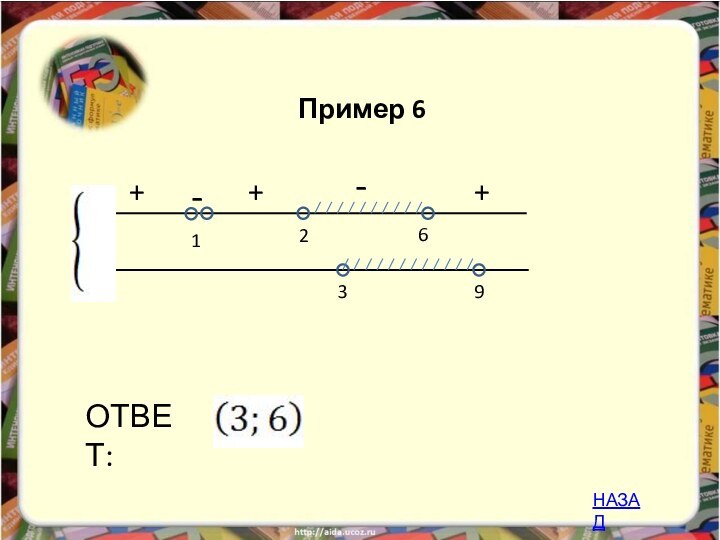
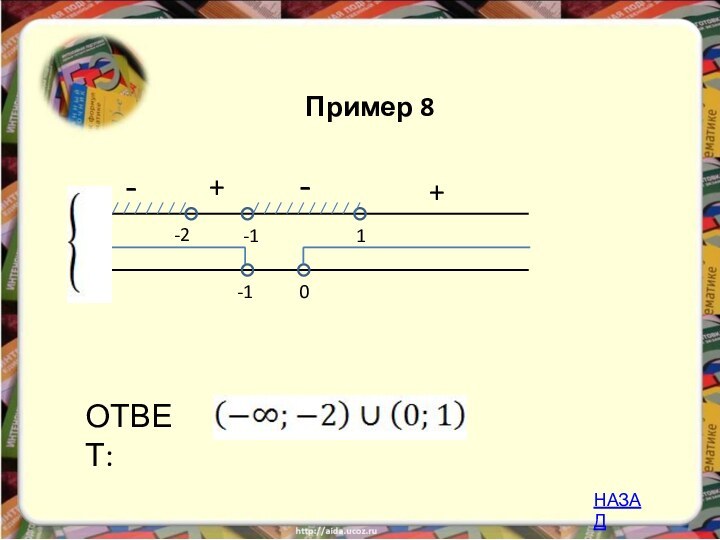
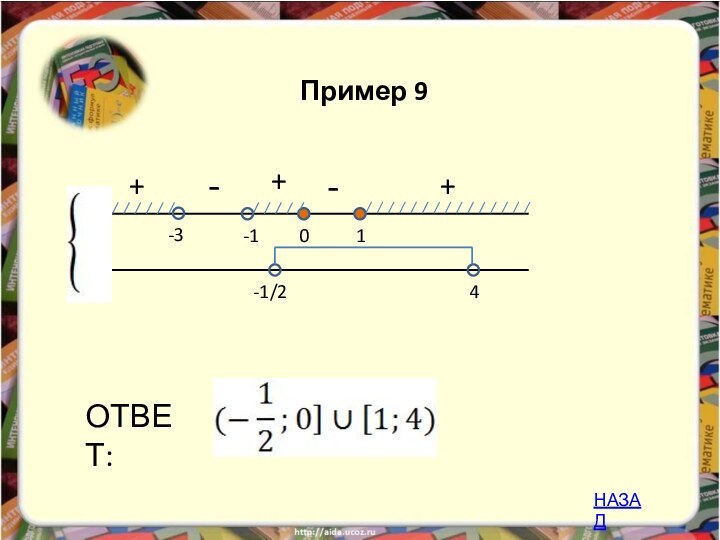
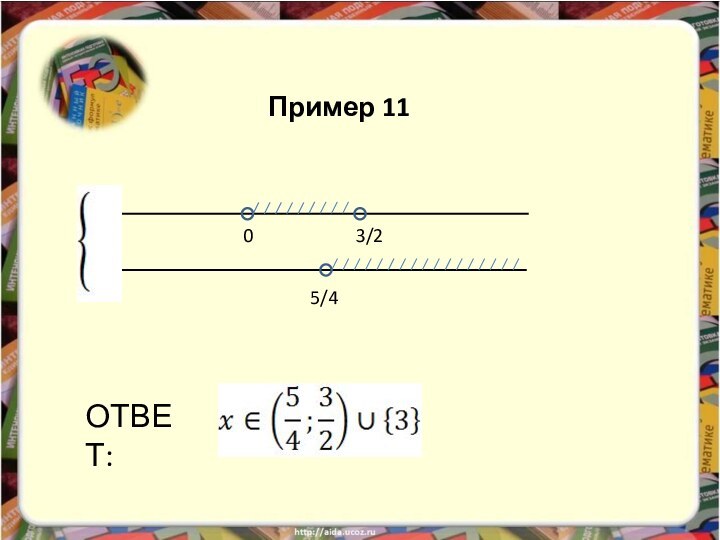
изучение математики невозможно без умения решать разнообразные неравенства, поэтому
мы решили рассмотреть один из способов решения неравенств – метод рационализации. В школьной программе он не изучается, но его применение значительно облегчает решение задания С3 ЕГЭ, в частности логарифмических и показательных неравенств.Введение