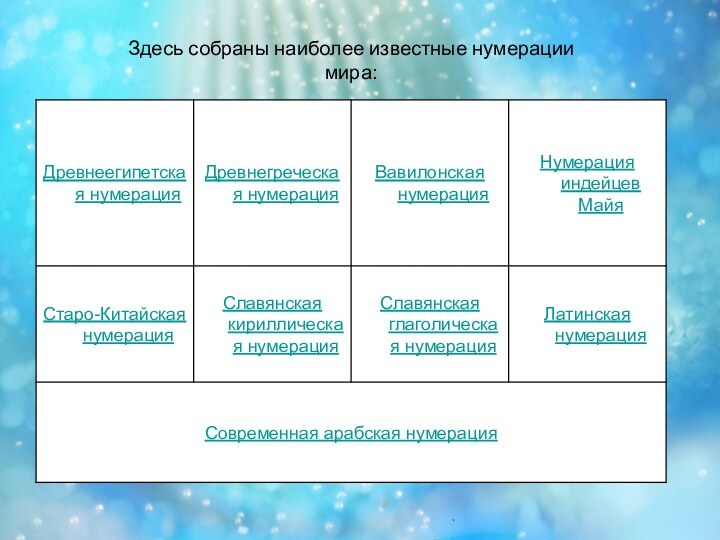
людей.
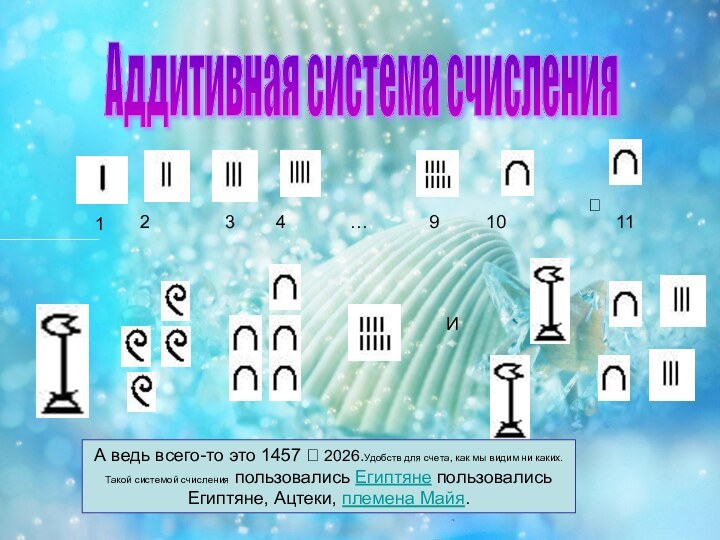
Аддитивная система счисления.
Алфавитная аддитивная система счисления.
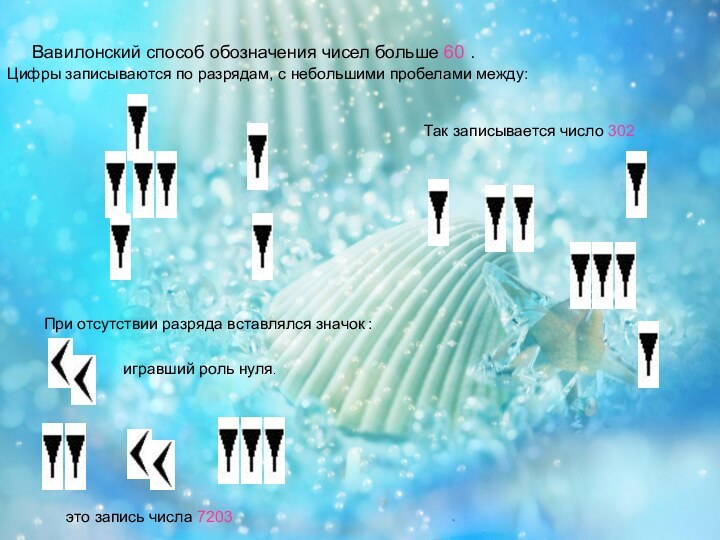
Мультипликативная система счисления.
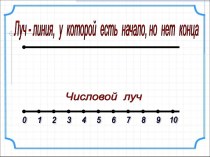
способ записи
чисел в позиционных системах счисления