Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Аппроксимация функций

Содержание

Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции.Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n:
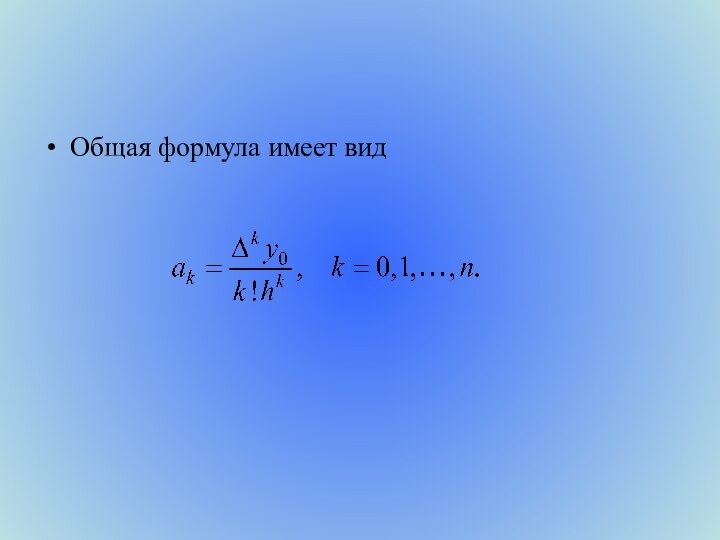
Аппроксимация функций (продолжение) Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции.Будем искать интерполяционный многочлен в виде При этом потребуем, чтобы каждый многочлен li(x) обращался в нуль во всех этим условиям при i = 0 отвечает многочлен видаДействительно, l0(x0) = 1. Аналогично……………………………………………………… Подставляя l0 , l1 ,…, ln в L(x) получимэта формула определяет интерполяционный многочлен Лагранжа. Из формулы для L(x)можно получить выражения для линейной (n = 1) и Существует несколько обобщений интерполяционного многочлена Лагранжа. интерполяционные многочлены Эрмита. Здесь наряду со Многочлен Ньютона. рассмотрим случай равноотстоящих значений аргумента, т. е. хi - хi-1 Введем понятие конечных разностей. Пусть известны значения функции в узлах Составим разности вторые разности функции: Аналогично составляются разности порядка k : Конечные разности можно выразить непосредственно через значения функции. Например, Аналогично для любого k можно написать Эту формулу можно записать и для Используя конечные разности, можно определить уk Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде: График многочлена должен проходить через заданные узлы, Найдем отсюда коэффициенты Общая формула имеет вид Подставляя эти выражения в формулу для N(x) получаем следующий вид интерполяционного многочлена Ньютона: Данную формулу часто записывают в другом виде. Для этого вводится переменная тогда тогда Полученное выражение называется первым интерполяционным многочленом Ньютона для интерполирования вперед. Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента [х0, Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае тогда Полученная формула называется вторым интерполяционным многочленом Ньютона для интерполирования назад.
Слайды презентации

Слайд 2 Многочлен Лагранжа.

Перейдем к случаю глобальной интерполяции.

Будем искать

Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции.Будем искать интерполяционный многочлен в

интерполяционный многочлен в виде линейной комбинации многочленов степени n:




Слайд 3 При этом потребуем, чтобы каждый многочлен li(x) обращался

При этом потребуем, чтобы каждый многочлен li(x) обращался в нуль во

в нуль во всех узлах интерполяции, за исключением одного

(i-го), где он должен быть равен единице.

Слайд 4 этим условиям при i = 0 отвечает многочлен

этим условиям при i = 0 отвечает многочлен видаДействительно, l0(x0) =

вида





Действительно, l0(x0) = 1.

При х = х1, х2,

... , хn числитель выражения обращается в нуль.

Слайд 5 Аналогично




………………………………………………………

Аналогично………………………………………………………

Слайд 6 Подставляя l0 , l1 ,…, ln в L(x)

Подставляя l0 , l1 ,…, ln в L(x) получимэта формула определяет интерполяционный многочлен Лагранжа.

получим






эта формула определяет интерполяционный многочлен Лагранжа.

Слайд 7 Из формулы для L(x)можно получить выражения для линейной

Из формулы для L(x)можно получить выражения для линейной (n = 1)

(n = 1) и квадратичной (n = 2) интерполяций:



Слайд 8 Существует несколько обобщений интерполяционного многочлена Лагранжа.
интерполяционные многочлены

Существует несколько обобщений интерполяционного многочлена Лагранжа. интерполяционные многочлены Эрмита. Здесь наряду

Эрмита.

Здесь наряду со значениями функции yi в узлах

xi задаются значения ее производной уi’.

Задача состоит в том, чтобы найти многочлен степени 2n + 1, значения которого и значения его производной в узлах xi удовлетворяют соответственно соотношениям

Слайд 9
Многочлен Ньютона.

рассмотрим случай равноотстоящих значений аргумента, т.

Многочлен Ньютона. рассмотрим случай равноотстоящих значений аргумента, т. е. хi -

е. хi - хi-1 = h = const (i

= 1,2,...,n).

Величина h называется шагом.

Слайд 10 Введем понятие конечных разностей.
Пусть известны значения функции

Введем понятие конечных разностей. Пусть известны значения функции в узлах Составим

в узлах
Составим разности значений функции:






Эти значения называются

первыми разностями (или разностями первого порядка) функции.

Слайд 11
вторые разности функции:



Аналогично составляются разности порядка k

вторые разности функции: Аналогично составляются разности порядка k :

Слайд 12
Конечные разности можно выразить непосредственно через значения функции.

Конечные разности можно выразить непосредственно через значения функции. Например,

Например,

Слайд 13


Слайд 14 Аналогично для любого k можно написать



Эту формулу

Аналогично для любого k можно написать Эту формулу можно записать и

можно записать и для значения разности в узле xi:


Слайд 15
Используя конечные разности, можно определить уk

Используя конечные разности, можно определить уk

Слайд 16
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен

Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде:

будем искать в следующем виде:

Слайд 17 График многочлена должен проходить через заданные узлы,

График многочлена должен проходить через заданные узлы,



Эти условия используем для нахождения коэффициентов многочлена:

Слайд 18
Найдем отсюда коэффициенты

Найдем отсюда коэффициенты

Слайд 19
Общая формула имеет вид

Общая формула имеет вид

Слайд 20
Подставляя эти выражения в формулу для N(x) получаем

Подставляя эти выражения в формулу для N(x) получаем следующий вид интерполяционного многочлена Ньютона:

следующий вид интерполяционного многочлена Ньютона:

Слайд 21
Данную формулу часто записывают в другом виде.
Для

Данную формулу часто записывают в другом виде. Для этого вводится переменная тогда

этого вводится переменная
тогда



Слайд 22
тогда




Полученное выражение называется первым интерполяционным многочленом Ньютона

тогда Полученное выражение называется первым интерполяционным многочленом Ньютона для интерполирования вперед.

для интерполирования вперед.

Слайд 23
Полученное выражение может аппроксимировать данную функцию на всем

Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента

отрезке изменения аргумента [х0, хn].


Однако с точки зрения

повышения точности расчетов более целесообразно использовать эту формулу для вычисления значении функции в точках левой половины рассматриваемого отрезка.

Слайд 24
Для правой половины отрезка [х0, хn]. разности лучше

Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае

вычислять справа налево.

В этом случае

  • Имя файла: approksimatsiya-funktsiy.pptx
  • Количество просмотров: 120
  • Количество скачиваний: 0
- Предыдущая Основные этапы накопления знаний о Земле
Следующая - Кроссворд Куликовская битва

Похожие презентации

Тест по математике Тест по математике 134
Решение неравенств второй степени с одной переменной Решение неравенств второй степени с одной переменной 85
Презентация по математике на тему:Число 12 Презентация по математике на тему:Число 12 183
Презентация к исследовательской работе Портрет моего класса в графиках и диаграммах2 Презентация к исследовательской работе Портрет моего класса в графиках и диаграммах2 97
В гостях у Шерлока Холмса и доктора Ватсона В гостях у Шерлока Холмса и доктора Ватсона 126
Конспект урока математики, 3 кл план-конспект урока по математике (3 класс) Конспект урока математики, 3 кл план-конспект урока по математике (3 класс) 97
Теорема Пифагора и различные способы её доказательства Теорема Пифагора и различные способы её доказательства 105
Презентация по математике и конструированию Развёртка куба (2кл) Презентация по математике и конструированию Развёртка куба (2кл) 93
Задачи на цену, количество, стоимость Задачи на цену, количество, стоимость 132
Презентация к внеклассному мероприятию Мисс Математика Презентация к внеклассному мероприятию Мисс Математика 76
Правильные многоугольники Правильные многоугольники 113
Типы иррациональных уравнений Типы иррациональных уравнений 90
Правильные многогранники Правильные многогранники 93
Групповая и парная работа в УМК Школа 21 века на примере урока математики во 2 классе Умножение числа 3 и деление на 3 презентация к уроку по математике (2 класс) Групповая и парная работа в УМК Школа 21 века на примере урока математики во 2 классе Умножение числа 3 и деление на 3 презентация к уроку по математике (2 класс) 153
Решение заданий С2 ЕГЭ-2010 Решение заданий С2 ЕГЭ-2010 96
Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число. методическая разработка по математике (4 класс) по теме Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число. методическая разработка по математике (4 класс) по теме 91
Урок математики презентация к уроку по математике (3 класс) Урок математики презентация к уроку по математике (3 класс) 100
Презентация по математике при изучении геометрических фигур. презентация по математике Презентация по математике при изучении геометрических фигур. презентация по математике 96
Презентация к уроку математики Сравнение долей презентация к уроку по математике (3 класс) Презентация к уроку математики Сравнение долей презентация к уроку по математике (3 класс) 109
Математика 4 класс. Уроки 18-19. Устные упражнения Математика 4 класс. Уроки 18-19. Устные упражнения 84
Презентация по математике на тему Уравнение Презентация по математике на тему Уравнение 84
Десять решений одной задачи Десять решений одной задачи 84
ПРОЕКТНЫЙ МЕТОД В ОБУЧЕНИИ МЛАДШИХ ШКОЛЬНИКОВ КАК СРЕДСТВО ФОРМИРОВАНИЯ УЧЕБНОЙ МОТИВАЦИИ В РАМКАХ СИСТЕМНО-ДЕЯТЕЛЬНОСТНОГО ПОДХОДА статья по математике (1,2,3,4 класс) ПРОЕКТНЫЙ МЕТОД В ОБУЧЕНИИ МЛАДШИХ ШКОЛЬНИКОВ КАК СРЕДСТВО ФОРМИРОВАНИЯ УЧЕБНОЙ МОТИВАЦИИ В РАМКАХ СИСТЕМНО-ДЕЯТЕЛЬНОСТНОГО ПОДХОДА статья по математике (1,2,3,4 класс) 32
Презентация Единицы длины презентация к уроку по математике (2, 3, 4 класс) Презентация Единицы длины презентация к уроку по математике (2, 3, 4 класс) 151
Занимательный урок по математике Сантиметр 1 класс презентация к уроку по математике (1 класс) по теме Занимательный урок по математике Сантиметр 1 класс презентация к уроку по математике (1 класс) по теме 27
Презентация Дециметр 1 класс Петерсен презентация к уроку по математике (1 класс) по теме Презентация Дециметр 1 класс Петерсен презентация к уроку по математике (1 класс) по теме 240
Таблица умножения на 6 презентация к уроку по математике (3 класс) Таблица умножения на 6 презентация к уроку по математике (3 класс) 79
Аттестационная работа. Программа по внеурочной деятельности Занимательная математика Аттестационная работа. Программа по внеурочной деятельности Занимательная математика 76
Решение текстовых задач с помощью умножения и деления Решение текстовых задач с помощью умножения и деления 114
Урок математики во 2 классе Сложение и вычитание чисел методическая разработка по математике (2 класс) Урок математики во 2 классе Сложение и вычитание чисел методическая разработка по математике (2 класс) 81