Презентация, доклад на тему Применение координатно-векторного метода к решению стереометрических задач (творческая работа обучающегося)

Применение координатно-векторного метода в решении стереометрических задач

Творческая работа ученика 11 «Г» класса Аткина Кирилла Руководитель – учитель математики Гришина Ирина Владимировна
 

Цели и задачи работы:

Изучить формулы и приемы координатно-векторного метода;
Провести классификацию стереометрических задач, к которым целесообразно применение координатно-векторного метода;

Освоить применение координатно-векторного метода решения стереометрических задач.

Классификация задач

Координатно-векторный метод удобен при решении задач на нахождение - углов между прямыми - углов между прямой и плоскостью - углов между плоскостями - расстояния от точки до плоскости - расстояния от точки до прямой - расстояния между скрещивающимися прямыми

a

b

a

b

p

q

q

p

φ

φ

ϴ

ϴ

Угол между двумя прямыми.

0 ⁰ ≤ ϴ ≤ 90⁰ φ = ϴ

90 ⁰ < ϴ ≤ 180⁰ φ =180⁰ - ϴ

cosφ=| cos ϴ |

1.)

2.)

Косинус угла между двумя прямыми равняется модулю косинуса угла между направляющими векторами данных прямых.

Угол между прямой и плоскостью.

α

φ

ϴ

α

a

a1

p

n

α

φ

ϴ

α

a

a1

p

n

0 ⁰ ≤ ϴ ≤ 90⁰ φ + ϴ = 90⁰

90 ⁰ < ϴ ≤ 180⁰ ϴ = 90⁰ + φ

1.)

2.)

sinφ=| cos ϴ |

Синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и вектором нормали к данной плоскости

α

α

α

β

α

n1

n2

φ

ϴ

Угол между двумя плоскостями.

Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей к данным плоскостям.

cosφ=| cosϴ |

α

α

β

n1

φ

n2

0 ⁰ ≤ ϴ ≤ 90⁰ φ = ϴ

90 ⁰ < ϴ ≤ 180⁰ φ =180⁰ - ϴ

ϴ

1.)

2.)

Расстояние от точки до плоскости.

α

B

M0

M1

b

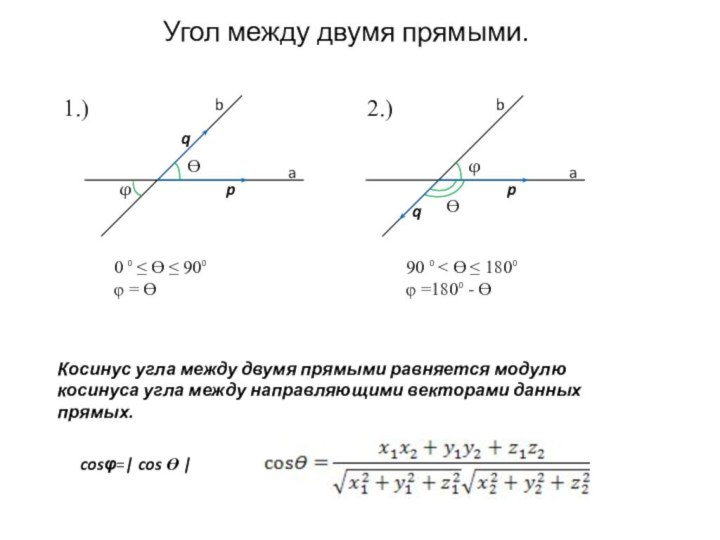
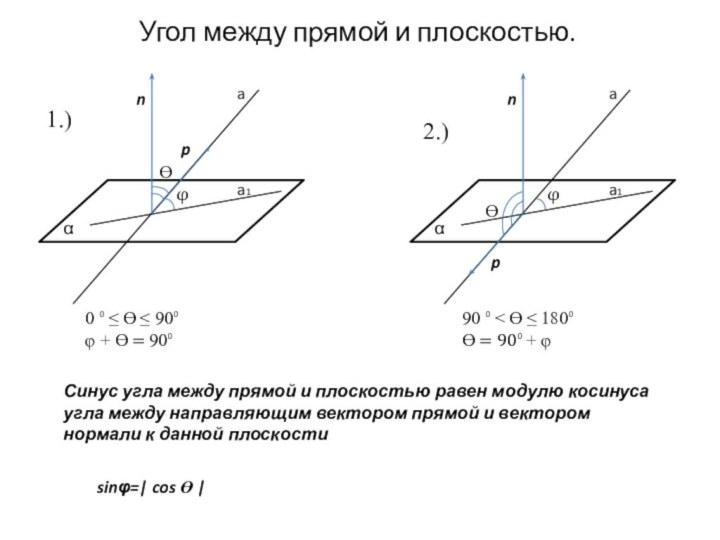
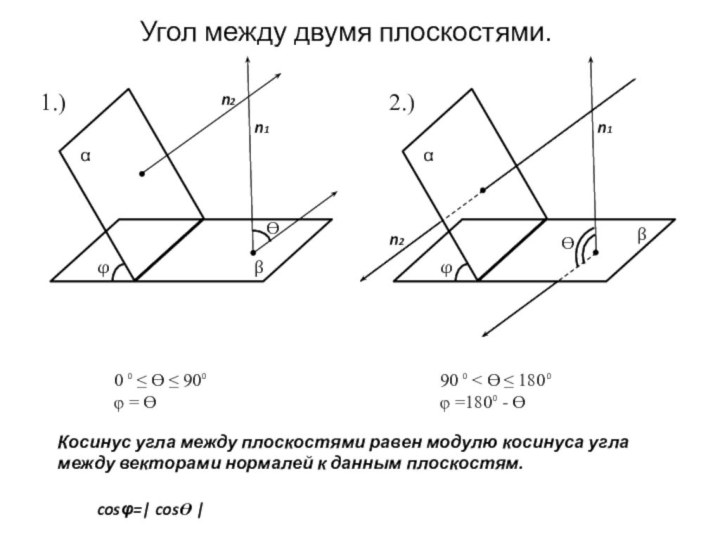
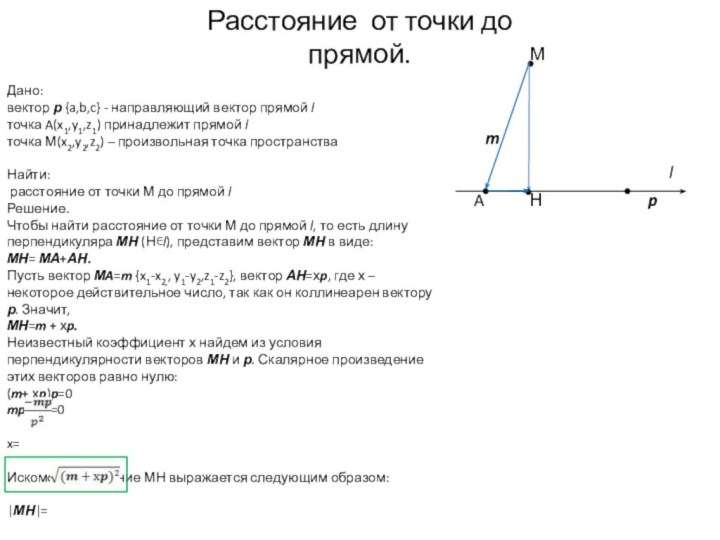
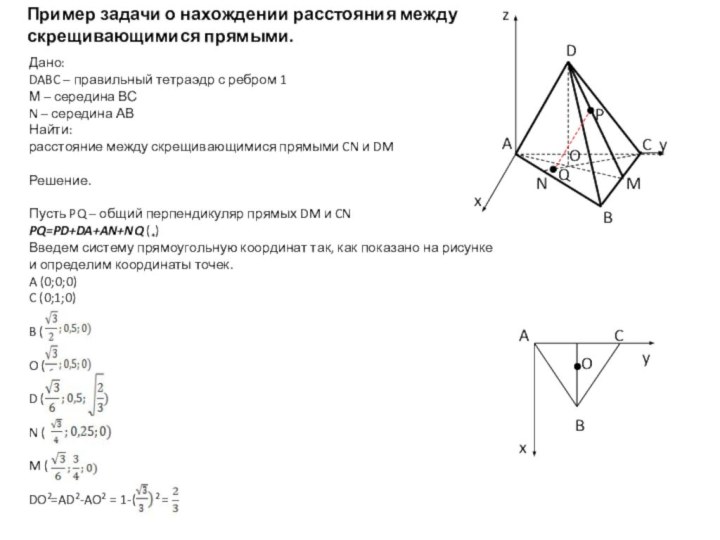
 Дано: α - плоскость, заданная уравнением ax+by+cz+d=0 M0(x0;y0;z0)

Найти: расстояние от M0 до плоскости α

Решение. Обозначим основание перпендикуляра, опущенного из точки М0 на плоскость α точкой М1 (x1;y1;z1). Поскольку точка М1 лежит в плоскости α, то ее координаты удовлетворяют уравнению данной плоскости: ax1+by1+cz1+d=0 (1) Вектор М0М1 (если не является нулевым), как и вектор n{a,b,c}, перпендикулярен к плоскости α, поэтому М0М1║n. Следовательно, существует такое число k, что M0M1= kn. 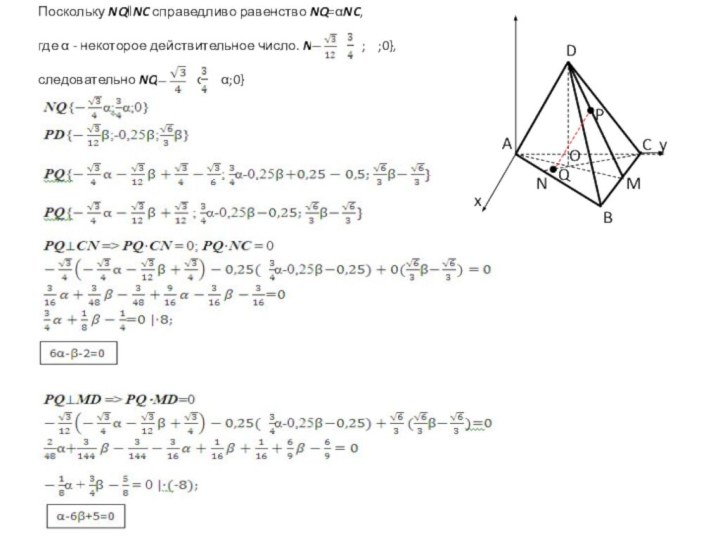Запишем это равенство в координатах: x1-x0=ka, y1-y0=kb, z1-z0=kc (2) Заметим, что искомое расстояние равно длине вектора М0М1, т.е. равно
l =
l =
l = |k| (3) Выразим теперь координаты точки М1 из уравнений(2) : x1=x0+ka y1=y0+kb z1=z0+kc
и подставим в уравнение (1):a(ka+x0)+b(kb+y0)+c(kc+z0)+d=0 ka²+x0a+kb²+y0b+kc²+z0c+d=0 k= - (4)
При подстановке уравнения(4) в уравнение(3) получаем: ρ(M0 ;α) = Полученная формула является формулой расстояния от точки М0(x0;y0;z0)
до плоскости α с вектором нормали к ней n{a,b,c}

α

 
Дано: вектор р {a,b,c} - направляющий вектор прямой l точка A(x1,y1,z1) принадлежит прямой l точка М(x2,y2,z2) – произвольная точка пространства
Найти: расстояние от точки М до прямой l
Решение.
Чтобы найти расстояние от точки М до прямой l, то есть длину перпендикуляра МН (Н∊l), представим вектор МН в виде: МН= МА+АН. Пусть вектор МA=m {x1-x2,, y1-y2,z1-z2}, вектор АН=хp, где х – некоторое действительное число, так как он коллинеарен вектору р. Значит, МН=m + хp. Неизвестный коэффициент х найдем из условия перпендикулярности векторов МН и р. Скалярное произведение этих векторов равно нулю: (m+ хp)p=0 mp+xp2=0 x=
Искомое расстояние МН выражается следующим образом: |МН|=

Расстояние от точки до прямой.

A

Н

М

p

m

l

α

α

A

B

M

N

a

b

Расстояние между скрещивающимися прямыми.

Дано:
Скрещивающиеся прямые a и b прямая a задана направляющим вектором р и точкой А(x1,y1,z1) прямая b задана направляющим вектором q и точкой B(x2,y2,z2) Найти: расстояние между прямыми a и b Решение.
Известно, что существует общий перпендикуляр двух скрещивающихся прямых, и притом
только один. Пусть это будет отрезок MN, концы которого M и N лежат на прямых a и b соответственно. Выразим вектор MN:
MN= MA+AB+BN. Так как векторы МА и ВN коллинеарны векторам p и q соответственно, то их можно представить в виде: МА=xp, BN=yq, где x и y – некоторые действительные числа
AB{x2-x1, y2-y1, z2-z1} = m. Тогда MN= m + хp + yq. Неизвестные коэффициенты x и y найдем из условий перпендикулярности вектора MN векторам p и q: MN∙p=0, MN∙q=0 В результате получается система линейных уравнений с двумя неизвестными x и y, решив которую, найдем x и y. ⟺ Искомое расстояние МN выражается следующим образом:
|МN|=

р

q

m

Р

Q

Пример задачи о нахождении расстояния от точки до прямой.
 
Дано:
ABCDA1B1C1D1 - единичный куб, где Р и Q – сере-
дины соответственно ребер A1B1 и ВС.
Найти: расстояние от точки D1 до прямой РQ,
 
Решение.
Рассмотрим прямоугольную
систему координат с началом в точке B, единичный отрезок равен ребру куба. Отметим на PQ точку H такую, что отрезок D1H –перпендикуляр к PQ Найдем координаты точек: P(0.5;0;1) Q(0;0.5;0) D1(1;1;1) B1(0;0;1) Тогда D1P{-0,5;-1;0} PQ{-0,5;0,5;-1} D1H = D1P + PH. Но PH коллинеарен PQ, поэтому PH=xPQ => PH{-0.5x;0.5x;-x} D1H{-0.5-0.5 x;-1+0.5 x;- x} D1H⊥PQ , поэтому D1H·PQ=0 0.25+0.25 x-0.5+0.25 x+ x=0 3/2 x -0.25=0 х=1/6. Вычисляем координаты вектора D1H, а затем его длину. D1H{-7/12;-11/12;-1/6}
D1H = =
Ответ: расстояние от точки D1 до прямой РQ равно .

A1

B1

C1

D1

A

B

C

D

x

z

y

H

Дано: DABC – правильный тетраэдр с ребром 1 М – середина ВС N – середина АВ Найти: расстояние между скрещивающимися прямыми CN и DM

Решение. Пусть PQ – общий перпендикуляр прямых DM и CN PQ=PD+DA+AN+NQ (*) Введем систему прямоугольную координат так, как показано на рисунке и определим координаты точек. A (0;0;0) C (0;1;0) B (
O ( D ( N ( M (
DO2=AD2-AO2 = 1-( 2 =

D

A

B

C

P

M

N

Q

x

z

y

A

B

C

x

y

O

O

Пример задачи о нахождении расстояния между скрещивающимися прямыми.

Поскольку NQ‖NC справедливо равенство NQ=αNC, где α - некоторое действительное число. NC { ; ;0}, следовательно NQ{ α; α;0}

D

A

B

C

P

M

N

Q

x

y

O

Ответ: расстояние между скрещивающимися прямыми CN и DM равно

Заключение
В работе проведена
- систематизация стереометрических задач, к решению которых возможно применение координатно-векторного метода;
- для каждой из рассмотренных задач приведено общее решение, выведена формула или показан общий подход к поиску решения;
-применение формул или общих подходов иллюстрируется с помощью примеров задач.
 
 
Координатно-векторный метод позволяет избежать сложных логических рассуждении и геометрических построений, что упрощает решение определенного класса задач на нахождение углов и расстояний в пространстве.