approach (S.Abramsky 1991)
2.ACP with recursion (J.A.Bergstra and J.W.Klop, 1984)
3.Coalgebraic
approach (P.Aczel, 1988, later B.Jecobs and J.Rutten) 4.Continuous algebras (A.Letichevsky,D.Gilbert,1997)
В теории автоматов:
Автомат есть транзиционная система, размеченная парами вход/выход
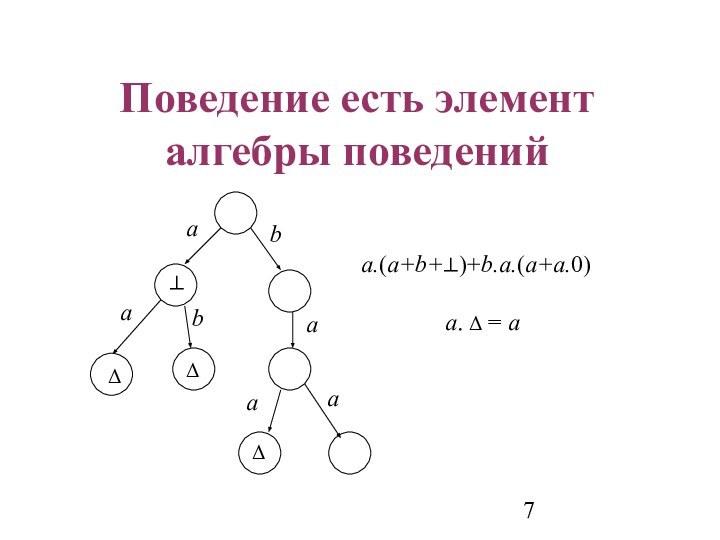
Поведение есть автоматное отображение
Или
Автомат есть настроенная транзиционная система, размеченная
входными символами
Поведение есть язык