Презентация, доклад Двоичная система счисления (9 класс)

Системы счисления. Двоичная система счисления.

История развития систем счисления

У первобытных народов не существовало развитой системы счисления. Ещё в 19 в. у многих племён Австралии и Полинезии было только два числительных: один и два; сочетания их образовывали числа: 3 — два-один, 4 — два-два, 5 — два-два-один и 6 — два-два-два. О всех числах, больших 6, говорили: “много”, не индивидуализируя их.

Египтяне впервые ввели десятичную систему счисления, правда без позиционного обозначения. В развитии математики в государствах ислама получила распространение десятичная позиционная система счисления с применением нуля, ведущая своё происхождение от индийской математики. Возникновение десятичной системы счисления связано со счётом на пальцах. Имелись системы счисления и с другим основанием: 5, 12 (счёт дюжинами), 20 (следы такой системы сохранились во французском языке, например quatre-vingts, то есть буквально четыре-двадцать, означает 80, 40, 60 и др. 

Вавилонские математики широко пользовались созданной ещё шумерами шестидесятеричной позиционной системой счёта; на основе этой системы были составлены различные вычислительные таблицы: деления и умножения чисел, квадратов и кубов чисел и их корней (квадратных и кубических).

Перевод чисел в 2, 8, 16 системы счисления

При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм:
1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю.
Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.

Перевод чисел из 2, 8, 16 системы счисления.
При переводе чисел из системы счисления с основанием P в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер –1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления

Системы счисления анатомического происхождения
Единичная Загнутый палец
Десятичная Пальцы обеих рук
Пятеричная Пальцы одной руки
Двенадцатеричная Фаланги 4 пальцев
Двадцатеричная Пальцы рук и ног

Алфавитные системы счисления
Славянская, Древнеармянская, Древнегрузинская, Древнегреческая (Ионическая)

Прочие
Римская, Вавилонская

«Машинные» системы счисления
Двоичная, Восьмеричная, Шестнадцатеричная

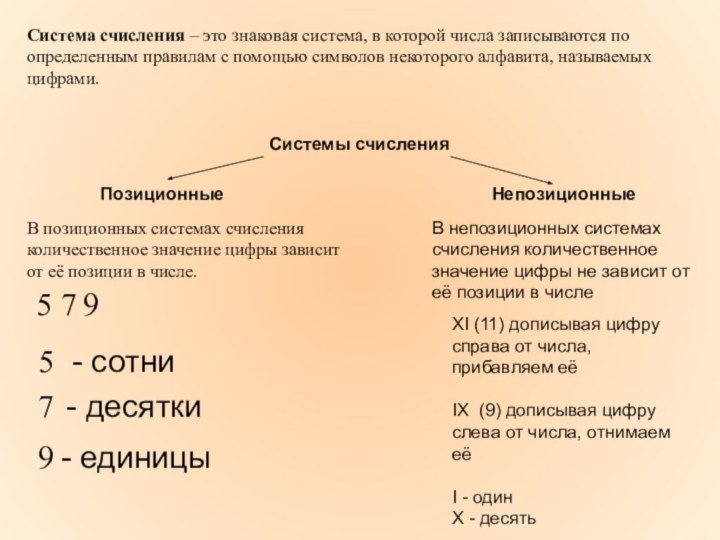
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Системы счисления

Непозиционные

Позиционные

В позиционных системах счисления количественное значение цифры зависит от её позиции в числе.

В непозиционных системах счисления количественное значение цифры не зависит от её позиции в числе

5

7

9

5

7

9

XI (11) дописывая цифру справа от числа, прибавляем её

IX (9) дописывая цифру слева от числа, отнимаем её

I - один
X - десять

- сотни

- десятки

- единицы

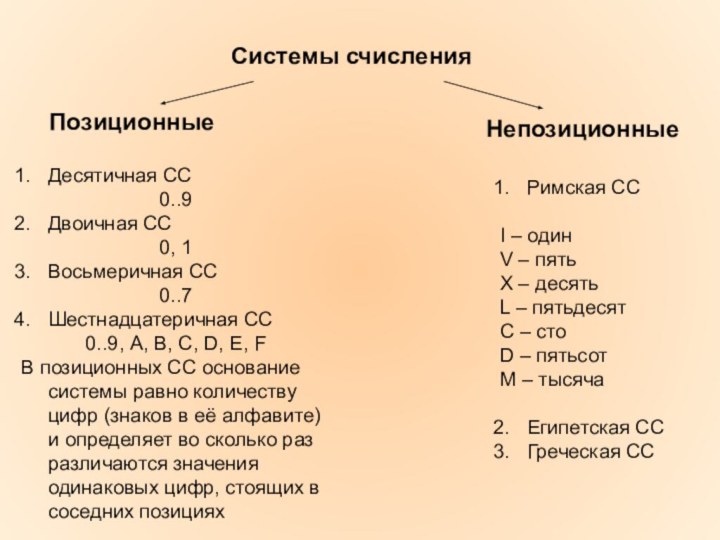
Системы счисления

Непозиционные

Позиционные

Десятичная СС
0..9
Двоичная СС
0, 1
Восьмеричная СС
0..7
Шестнадцатеричная СС
0..9, А, В, С, D, E, F
В позиционных СС основание системы равно количеству цифр (знаков в её алфавите) и определяет во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях

Римская СС

I – один
V – пять
X – десять
L – пятьдесят
C – сто
D – пятьсот
M – тысяча

Египетская СС
Греческая СС

Боцуляк Т.П.
2016

Табличные вычисления на компьютере

План урока

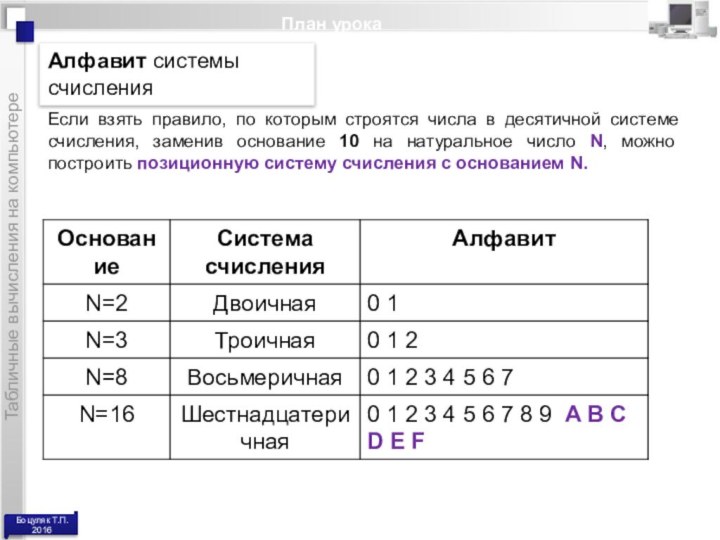
Алфавит системы счисления

Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.

6

2

3

0

12

-

6

2

26

13

2

Перевод целых чисел из десятичной СС в двоичную СС.

Алгоритм перевода:

Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.

Записать полученные остатки в обратной последовательности.

27

-

1

1

-

2

-

2

1

1

Перевод целых чисел из двоичной СС в десятичную СС.

=

Алгоритм перевода:
Двоичное число записать в РАЗВЕРНУТОЙ ФОРМЕ.
Произвести вычисления.

0

1

2

3

4

5

6

7

Примеры для закрепления изученного материала

Боцуляк Т.П.
2016

Табличные вычисления на компьютере

План урока

Перевод чисел из десятичной системы счисления в двоичную

Примеры:

13110 =

7910 =

12410 =

6810 =

100000112

11111002

10011112

10001002

Боцуляк Т.П.
2016

Табличные вычисления на компьютере

План урока

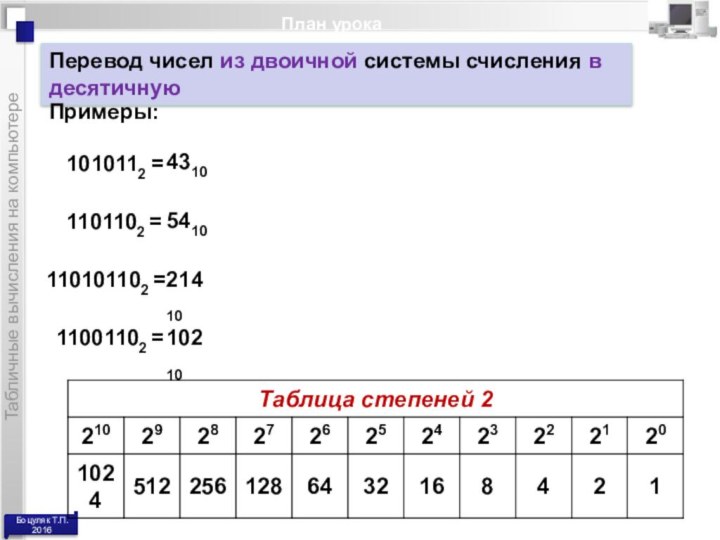
Перевод чисел из двоичной системы счисления в десятичную

Примеры:

1010112 =

1101102 =

4310

5410

110101102 =

21410

11001102 =

10210

Арифметика двоичных чисел

сложение

0+0=0 0+1=1
1+0=1 1+1=102
1 + 1 + 1 = 112

1 0 1 1 02
+ 1 1 1 0 1 12

1

0

0

0

1

1

0

2

1

1

1

1

1

10011002

10001012

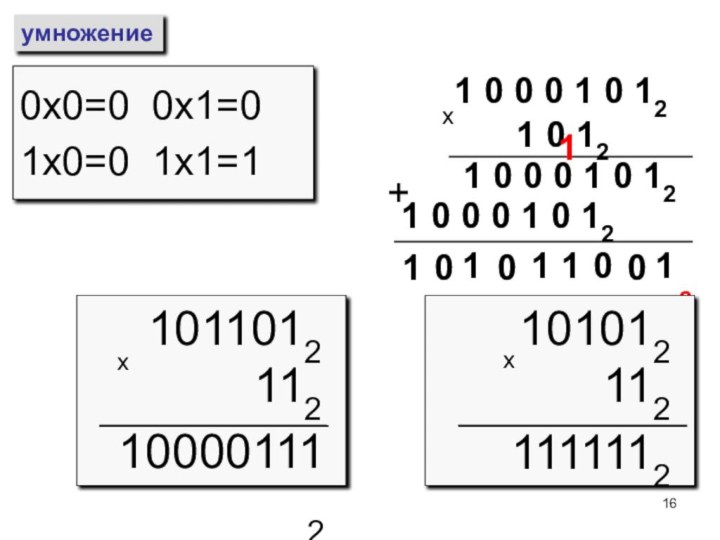
умножение

0х0=0 0х1=0
1х0=0 1х1=1

1 0 0 0 1 0 12
1 0 12

1 0 0 0 1 0 12

х

+

1 0 0 0 1 0 12

1

0

0

1

1

1

0

1

0

1

2

х

х

100001112

1111112

Соответствие десятичной и двоичной систем счисления

Количество используемых цифр называется основанием системы счисления.

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:
12310 — это число 123 в десятичной системе счисления;
11110112 — то же число, но в двоичной системе.
Двоичное число 1111011 можно расписать в виде: 11110112 = 1*26 + 1*25 + 1*24 + 1*23 + 0*22 + 1*21 + 1*20.

Домашнее задание.
Решить следующие примеры:

Развернутая запись числа

Десятичная СС

Двоичная СС

ЧАСЫ
В ДВОИЧНОЙ
СИСТЕМЕ
СЧИСЛЕНИЯ