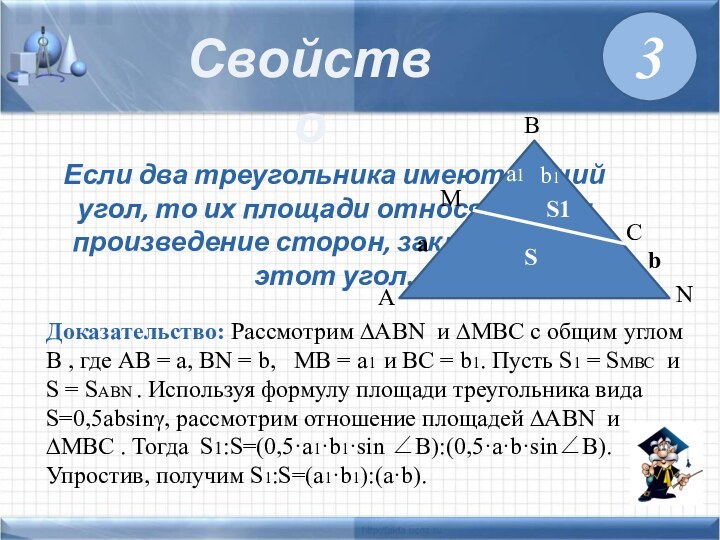
считаются геометрические задачи.
При решении геометрических
задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи. Один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.