- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия 8 класса в одной задаче
Содержание
- 2. показать многообразие подходов при решении одной геометрической задачи и найти более рациональный способ решения.Цель работы:
- 3. ЗадачаНайти площадь трапеции,
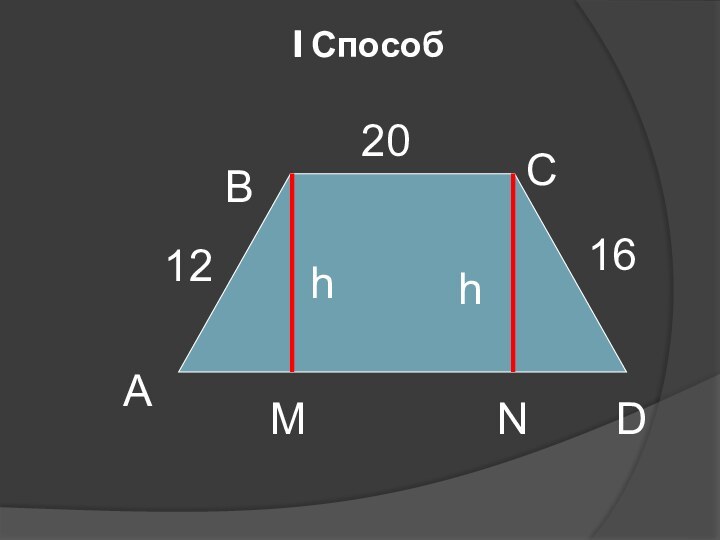
- 4. I СпособАМNDСВhh162012
- 5. а S АВСД = Так как S
- 6. II СпособАDВСКN 201216хh20-x16
- 7. Решение: Пусть ВN
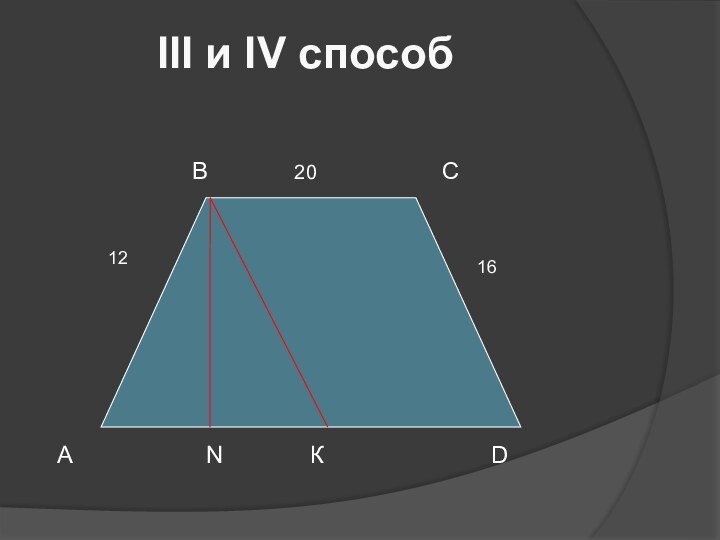
- 8. III и IV способ
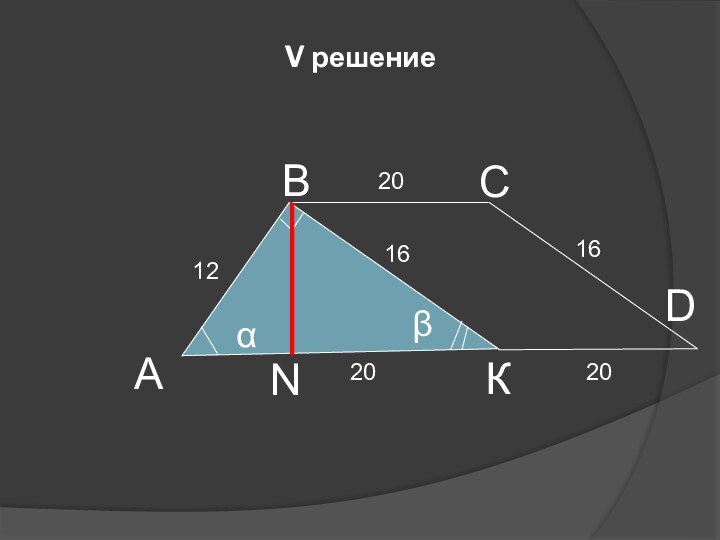
- 9. V решениеАВКNαβ1216CD20162020
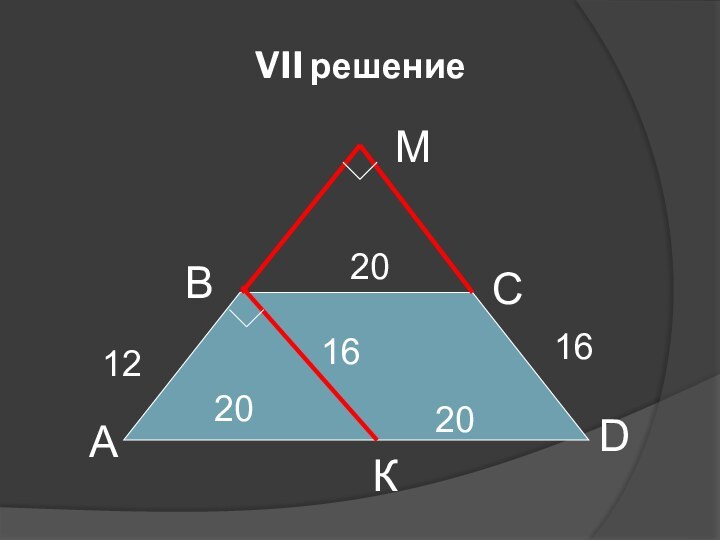
- 10. VII решениеАВСDМ202016162012К
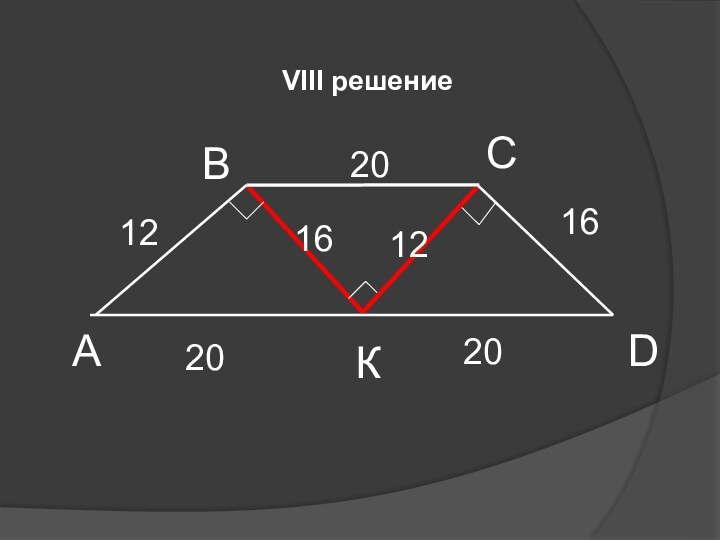
- 11. VIII решениеАВСDК12162016122020
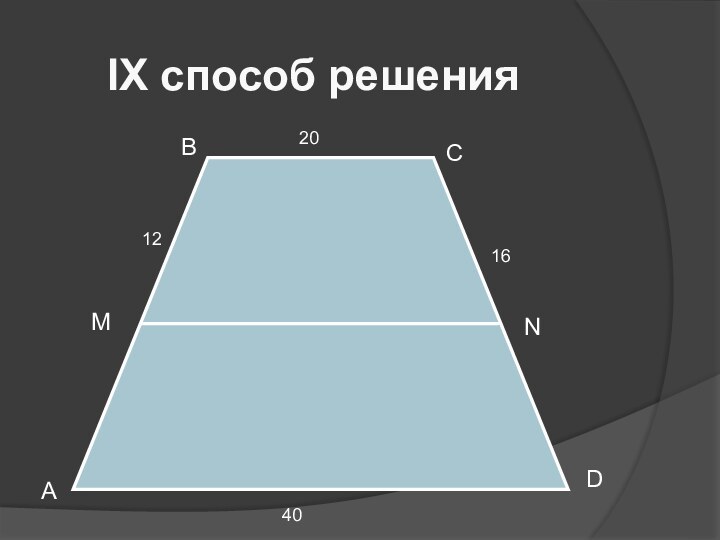
- 12. IХ способ решенияBCADMN20161240
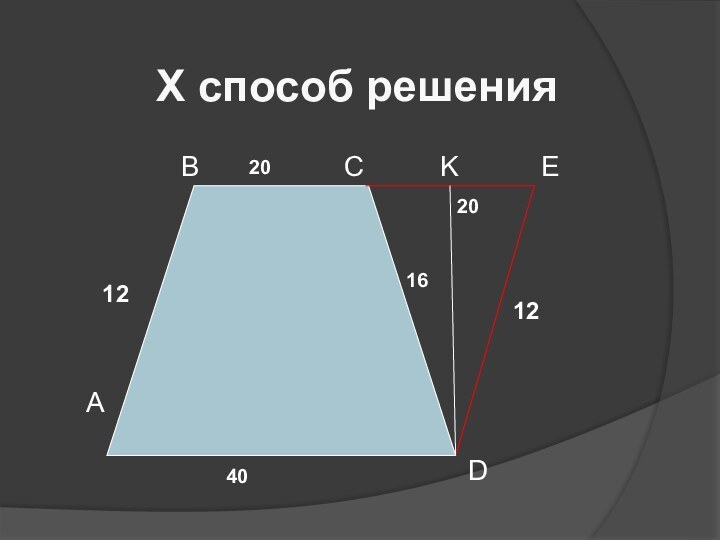
- 13. АХ способ решения
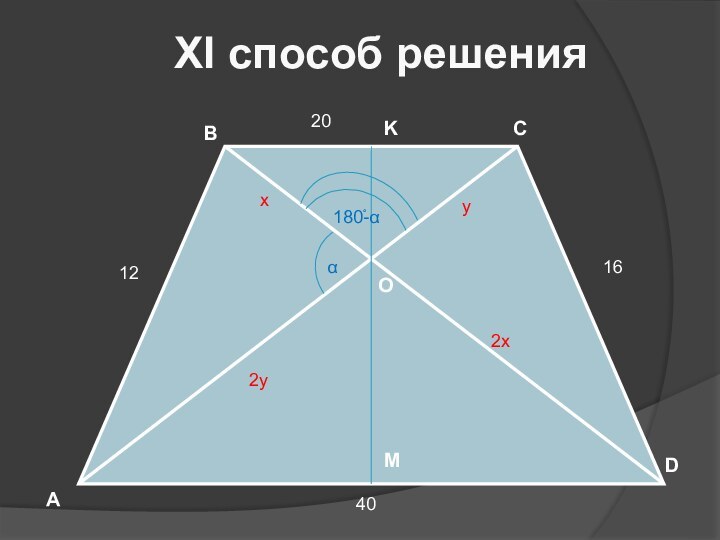
- 14. DXI способ решения
- 15. Скачать презентацию
- 16. Похожие презентации
показать многообразие подходов при решении одной геометрической задачи и найти более рациональный способ решения.Цель работы:







Слайд 2 показать многообразие подходов при решении одной геометрической задачи
и найти более рациональный способ решения.
Слайд 3
Задача
Найти площадь трапеции, основания
которой равны 40 см и 20см, а боковые стороны
12 см и 16 см.
Слайд 5
а S АВСД =
Так как S АВСD=
,то задача сводится к нахождению высоты H.
Решение:
Проведем отрезки ВМ
и СN так, что ВМ┴АD и СN┴АD, тогда ВСNМ – прямоугольник. Поэтому ВМ = СN и ВС = МN. Но в таком случае АМ + ND =20
Пусть АМ = х (см), тогда ND = 20 – х (см).
По теореме Пифагора из ▲АВМ и ▲СND: Н² = 12² - х² и Н² =16² - (20 – х) ².
Составим равенство 12² - х² = 16² - (20 – х) ², 144 - х² = 256 – 400 + 40х - х² , 40х = 288, х = 7,2 (см ).
Находим высоту Н: Н² = 12² – 7,2² = 144 – 51,84 = 92,16, Н =
Тогда S АВСD=
Ответ: 288(см²)
Слайд 7
Решение:
Пусть ВN ┴АD
и ВК║СD, тогда ВСDК – параллелограмм.
Значит ВК =
СD = 16 (см), КD = ВС = 20 (см).Пусть АN = х (см), тогда NК = (20 –х) см.
Выразим высоту Н из треугольников АВN и ВNК по теореме Пифагора:
Н² = 12² - х² и Н² =16² - (20 – х) ².
Составим равенство 12² - х² = 16² - (20 – х) ², 144 - х² = 256 – 400 + 40х - х² , 40х = 288, х = 7,2 (см ).
Н = 9,6см.
Значит площадь трапеции S АВСD = (см²).
Ответ: 288 см²