Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии Вычисление расстояния от точки до плоскости методом координат

Содержание

14 (C2). Стереометрическая задача
Решение задач на вычисление расстояния от прямой до плоскости методом координат Учитель 14 (C2). Стереометрическая задача Координаты вектора Длина вектораСкалярное произведение векторовСкалярное произведение векторов в координатахСвойство скалярного произведения Расстояние от точки до плоскостиПусть плоскость задана уравнением: ах + Задача 514245В правильной четырёхугольной пирамиде SABCD все рёбра равны 5. На рёбрах SA, AB, BC взяты точки P, Q, R соответственно Задача 514245552221) Введём прямоугольную систему координат.Найдём координаты точек А, В, С, D, Задача 514245552223) Пусть О – центр основания пирамиды.Найдём координаты точки О. Задача 514245554) Найдём координаты точки S.Отрезок SО – высота правильной пирамиды, тогда Задача 514245555) Найдём координаты точки Р.Проведём Задача 51424555ухОПрямоугольные треугольники АМО и АЕН подобны по двум углам, тогда т.е.Р2НСОЕН25Итак, Задача 51424555222Координаты точек:А(0;0;0), В(5;0;0), C(5;5;0), D(0;5;0), Q(2;0;0), R(5;3;0), О(2,5;2,5;0), Задача 514245 ухНайдём скалярное произведение векторовтогда прямые иИтак, прямая SD Задача 5142452 ухНайдём расстояние от точки D до плоскости РQR.Запишем Задача 514245 ухQ(2;0;0), R(5;3;0), В уравнение плоскости подставим координаты точек:Получили Задача 514245 ухНайдём расстояние от точки D(0;5;0) до плоскости РQR, В правильной треугольной призме  АВСА1В1С1 все рёбра равны 2. Точка M — середина ребра АА1 Задача 519659б) Найдем расстояние между прямыми MB и В1С. Прямые MB и В1С являются скрещивающимися. Расстоянием между скрещивающимися Задача 519659б) Введём прямоугольную систему координат. Нам необходимо задать уравнение плоскость МВХ Задача 519659Х(х;у;0)Найдём х и у. Рассмотрим векторы иВекторы Задача 519659Зададим плоскость ВМХ уравнением:М(0;0;1), в уравнение плоскости ах + bу + Задача 519659Уравнение плоскости ВМХ :где Координаты точки С: С(0;2;0).Найдём расстояние от точки
Слайды презентации

Слайд 2 14 (C2). Стереометрическая задача

14 (C2). Стереометрическая задача

Слайд 3 Координаты вектора
Длина вектора
Скалярное произведение векторов
Скалярное произведение векторов

Координаты вектора Длина вектораСкалярное произведение векторовСкалярное произведение векторов в координатахСвойство скалярного

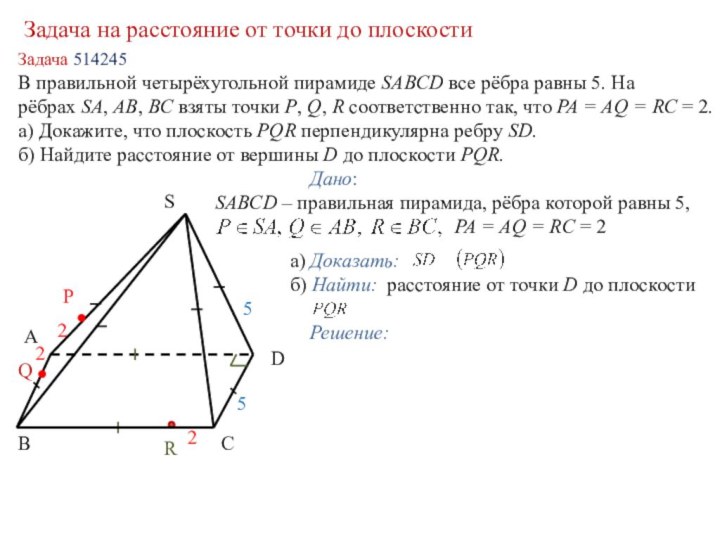
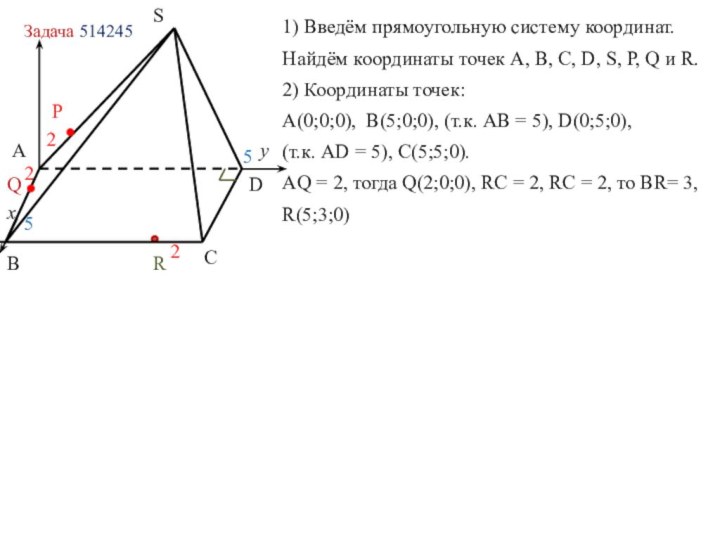
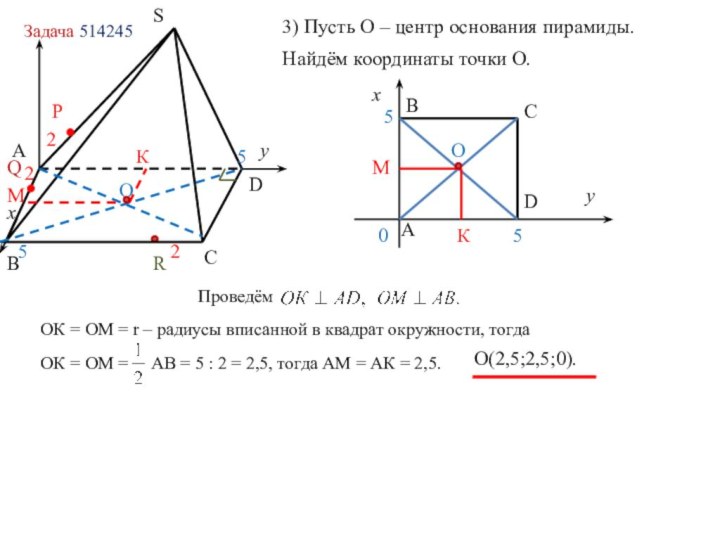
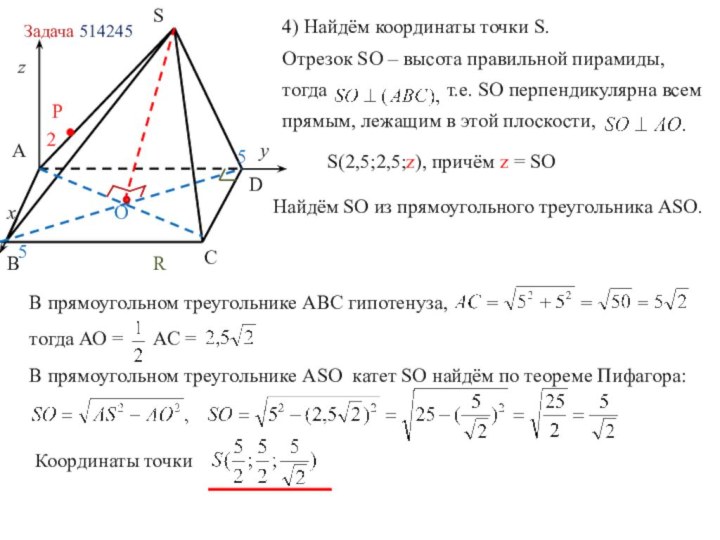
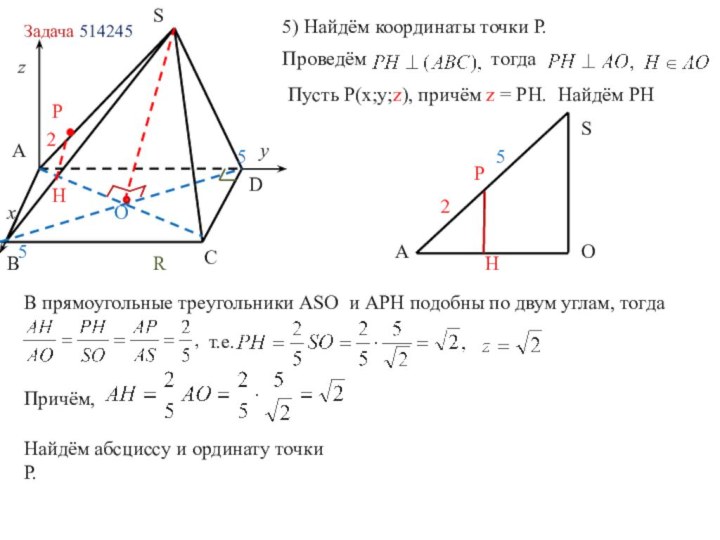
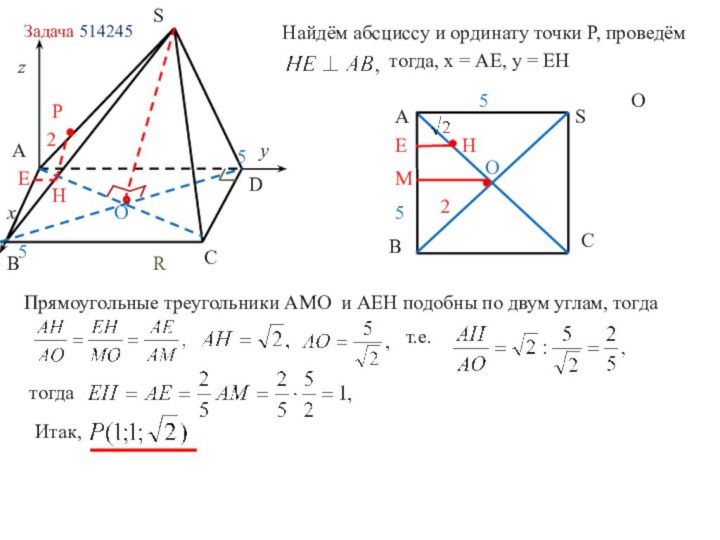
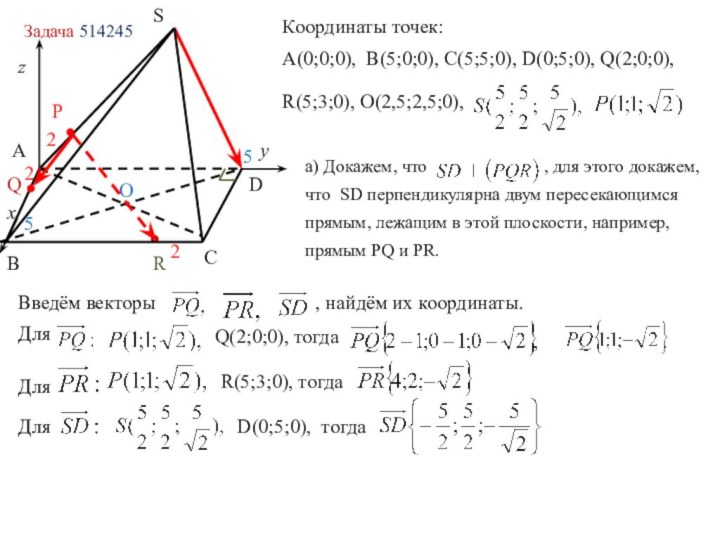
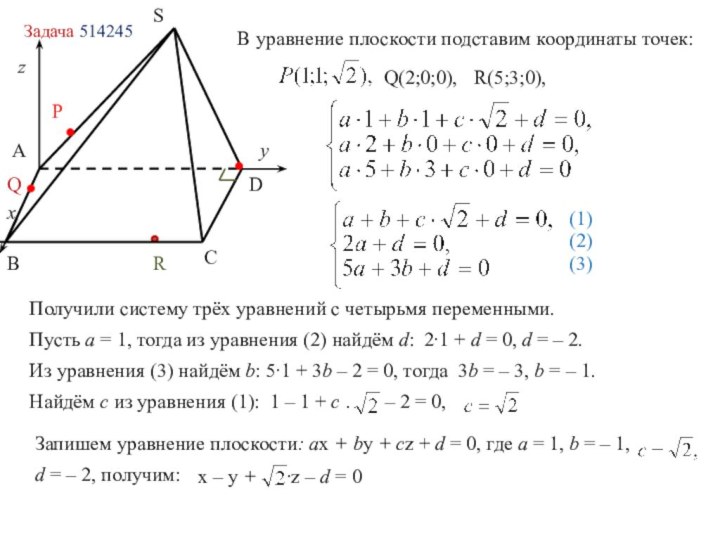
в координатах
Свойство скалярного произведения взаимно перпендикулярных векторов
Свойство координат коллинеарных

векторов
Угол между векторами

Слайд 4 Расстояние от точки до плоскости
Пусть плоскость

Расстояние от точки до плоскостиПусть плоскость задана уравнением: ах +

задана уравнением: ах + bу + сz + d

= 0.
Дана точка М(х0,у0,z0).
Расстояние от точки М до плоскости можно вычислить по формуле:

Слайд 5 Задача 514245
В правильной четырёхугольной пирамиде SABCD все рёбра равны 5.

Задача 514245В правильной четырёхугольной пирамиде SABCD все рёбра равны 5. На рёбрах SA, AB, BC взяты точки P, Q, R

На рёбрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA = AQ = RC = 2.
а) Докажите, что

плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.

Задача на расстояние от точки до плоскости

А

В

С

S

5

5

Q

R

Р

Дано:
SABCD – правильная пирамида, рёбра которой равны 5,
PA = AQ = RC = 2

а) Доказать:
б) Найти: расстояние от точки D до плоскости

Решение:

D

2

2

2

Слайд 6 Задача 514245

5
5
2
2
2
1) Введём прямоугольную систему координат.
Найдём координаты точек

Задача 514245552221) Введём прямоугольную систему координат.Найдём координаты точек А, В, С,

А, В, С, D, S, Р, Q и R.
2)

Координаты точек:
А(0;0;0), В(5;0;0), (т.к. АВ = 5), D(0;5;0),
(т.к. АD = 5), C(5;5;0).
АQ = 2, тогда Q(2;0;0), RС = 2, RС = 2, то ВR= 3,
R(5;3;0)





у

х

Слайд 7 Задача 514245

5
5
2
2
2
3) Пусть О – центр основания пирамиды.
Найдём

Задача 514245552223) Пусть О – центр основания пирамиды.Найдём координаты точки О.

координаты точки О.









у
х
О
у
х
О
5
5
А
С
D
В
К
М
К
М
0
Проведём
ОК

= ОМ = r – радиусы вписанной в квадрат окружности, тогда

ОК = ОМ = АВ = 5 : 2 = 2,5, тогда АМ = АК = 2,5.

О(2,5;2,5;0).

Слайд 8 Задача 514245

5
5
4) Найдём координаты точки S.
Отрезок SО –

Задача 514245554) Найдём координаты точки S.Отрезок SО – высота правильной пирамиды,

высота правильной пирамиды, тогда

т.е. SО перпендикулярна всем прямым, лежащим в этой плоскости,










у

х

О

В прямоугольном треугольнике АВС гипотенуза,

тогда АО = АС =

S(2,5;2,5;z), причём z = SО

Найдём SО из прямоугольного треугольника АSО.

В прямоугольном треугольнике АSО катет SО найдём по теореме Пифагора:

Координаты точки

Р

2

z

Слайд 9 Задача 514245

5
5
5) Найдём координаты точки Р.
Проведём

Задача 514245555) Найдём координаты точки Р.Проведём

тогда










у

х

О

Пусть Р(х;у;z), причём z = РН.

Найдём РН

В прямоугольные треугольники АSО и АРН подобны по двум углам, тогда

т.е.

Р

2

Н

S

О

А

Р

Н

2

5

Причём,

Найдём абсциссу и ординату точки Р.

z

Слайд 10 Задача 514245

5
5
у
х
О
Прямоугольные треугольники АМО и АЕН подобны по

Задача 51424555ухОПрямоугольные треугольники АМО и АЕН подобны по двум углам, тогда

двум углам, тогда

т.е.
Р
2
Н
С
О
Е
Н
2
5
Итак,
Найдём абсциссу и ординату точки

Р, проведём

Е

А

В

S

5

тогда, х = АЕ, у = ЕН

М

О

тогда

z

Слайд 11 Задача 514245

5
5
2
2
2
Координаты точек:
А(0;0;0), В(5;0;0), C(5;5;0), D(0;5;0), Q(2;0;0),

R(5;3;0),

Задача 51424555222Координаты точек:А(0;0;0), В(5;0;0), C(5;5;0), D(0;5;0), Q(2;0;0), R(5;3;0), О(2,5;2,5;0),

О(2,5;2,5;0),





у
х
О
а) Докажем, что

, для этого докажем,
что SD перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости, например,
прямым РQ и РR.

Введём векторы , найдём их координаты.
Для

Q(2;0;0), тогда

Для

R(5;3;0), тогда

Для

D(0;5;0), тогда

z

Слайд 12 Задача 514245







у
х
Найдём скалярное произведение

Задача 514245 ухНайдём скалярное произведение векторовтогда прямые иИтак, прямая SD

векторов
тогда прямые
и
Итак, прямая SD перпендикулярна двум пересекающимся прямым

плоскости
РQR, а значит,

тогда

Найдём скалярное произведение векторов

и

тогда

тогда прямые

z

Слайд 13 Задача 514245

2






у
х
Найдём расстояние от

Задача 5142452 ухНайдём расстояние от точки D до плоскости РQR.Запишем

точки D до плоскости РQR.
Запишем уравнение плоскости, проходящей через

точки

Расстояние от точки

Причём,

D(х0,у0,z0) до плоскости

, заданной уравнением

можно вычислить по формуле:

ах + bу + сz + d = 0

D(0;5;0).

Q(2;0;0),

R(5;3;0),

В уравнение плоскости подставим координаты точек.

z

Слайд 14 Задача 514245







у
х
Q(2;0;0),
R(5;3;0),
В

Задача 514245 ухQ(2;0;0), R(5;3;0), В уравнение плоскости подставим координаты точек:Получили

уравнение плоскости подставим координаты точек:
Получили систему трёх уравнений с

четырьмя переменными.
Пусть а = 1, тогда из уравнения (2) найдём d: 2∙1 + d = 0, d = – 2.
Из уравнения (3) найдём b: 5∙1 + 3b – 2 = 0, тогда 3b = – 3, b = – 1.
Найдём с из уравнения (1): 1 – 1 + с – 2 = 0,

(1)

(2)

(3)

Запишем уравнение плоскости: ах + bу + сz + d = 0, где а = 1, b = – 1,
d = – 2, получим:

х – у + ∙z – d = 0

z

Слайд 15 Задача 514245







у
х
Найдём расстояние от

Задача 514245 ухНайдём расстояние от точки D(0;5;0) до плоскости РQR,

точки D(0;5;0) до плоскости
РQR, заданной уравнением

х

– у + ∙z – d = 0

где х0 =0, у0 =5, z0 =0, а = 1, b = – 1, d = – 2, получим:

Ответ: расстояние от точки D до плоскости РQR равно 3,5

z

Слайд 16 В правильной треугольной призме  АВСА1В1С1 все рёбра равны

В правильной треугольной призме  АВСА1В1С1 все рёбра равны 2. Точка M — середина

2.
Точка M — середина ребра АА1 .
а) Докажите, что прямые MB и ВС1  перпендикулярны.
б)

Найдите расстояние между прямыми MB и В1С.

Задача на расстояние между скрещивающимися прямыми

Задача 519659

Дано:
АВСА1В1С1 – правильная пирамида, рёбра которой равны 2, M — середина АА1
а) Доказать: MB   ВС1 .
б) Найти: расстояние между прямыми MB и В1С.

Решение:
б) Найдем расстояние между прямыми MB и В1С.

А

В

С

С1

А1

В1

М

2

2

Слайд 17 Задача 519659
б) Найдем расстояние между прямыми MB и В1С. Прямые MB и В1С являются

Задача 519659б) Найдем расстояние между прямыми MB и В1С. Прямые MB и В1С являются скрещивающимися. Расстоянием между

скрещивающимися. Расстоянием между скрещивающимися прямыми является расстояние от одной

из этих прямых до плоскости, содержащей другую прямую, и параллельную первой.
Построим плоскость, параллельную прямой В1С, проходящую через прямую MB.

Х

Проведём прямую МХ, параллельную прямой В1С. Тогда по признаку параллельности прямой и плоскости прямая В1С параллельна плоскости MBХ.
Найдем расстояние от прямой В1С до плоскости MBХ, для этого на прямой В1С выберем точку, например, точку С, найдём расстояние от точки С до плоскости MBХ по формуле:

Слайд 18 Задача 519659
б) Введём прямоугольную систему координат.
Нам необходимо

Задача 519659б) Введём прямоугольную систему координат. Нам необходимо задать уравнение плоскость

задать уравнение плоскость МВХ и найти координаты точки С.
Найдём

координаты точек: С(0;2;0), М(0;0;1).
Пусть Х - точка пересечения прямых МХ и ВС, тогда
Х(х;у;0).
Найдём х и у. Рассмотрим векторы и
Найдём их координаты.

А

В

С1

А1

В1

М

2

2

Х

С

у

х

z

Найдём координаты точки В.

Треугольник АВС – равносторонний, со стороной 2.

А

С

В

Н

Проведём ВН – высоту треугольника, АН = 1, тогда по теореме Пифагора .
координаты точки В:
Тогда координаты точки В1:

2

1

Н

х

у

2

0

Слайд 19 Задача 519659
Х(х;у;0)
Найдём х и у. Рассмотрим векторы

Задача 519659Х(х;у;0)Найдём х и у. Рассмотрим векторы иВекторы лежат

и
Векторы лежат на параллельных прямых, а

значит коллинаерны, тогда их координаты пропорциональны.
Найдём координаты векторов и
Для :
Для : М(0;0;1), Х(х;у;0), тогда
Учитывая коллинеарность векторов, получаем:


А

В

С1

А1

В1

М

2

2

Х

С

у

х

z

С(0;2;0), тогда

Из равенства находим . Из равенства находим

Получаем координаты точки Х:

Слайд 20 Задача 519659
Зададим плоскость ВМХ уравнением:
М(0;0;1),
в уравнение плоскости

Задача 519659Зададим плоскость ВМХ уравнением:М(0;0;1), в уравнение плоскости ах + bу

ах + bу + сz + d = 0
подставим

координаты точек:



А

В

С1

А1

В1

М

2

2

Х

С

у

х

z

∙2

Пусть с = 1, тогда d = -1, из равенств (2) и (3), сложив их, получаем:

(2)

(1)

(3)

Из равенства (1) найдём а:

  • Имя файла: prezentatsiya-po-geometrii-vychislenie-rasstoyaniya-ot-tochki-do-ploskosti-metodom-koordinat.pptx
  • Количество просмотров: 263
  • Количество скачиваний: 8
- Предыдущая Презентация по географии С детства знакомые названия
Следующая - Выпускной квалификационной работы по специализации: Скоростно-силовая способность борца вольного стиля высокой квалификации

Похожие презентации

Симметрия относительно прямой Симметрия относительно прямой 149
Масштабы ГОСТ 2.302 -68 Масштабы ГОСТ 2.302 -68 143
Презентация к уроку по геометрии на тему Площадь параллелограмма (8 класс) Презентация к уроку по геометрии на тему Площадь параллелограмма (8 класс) 124
Площадь. Объём Площадь. Объём 172
Теорема Пифагора в картинках Теорема Пифагора в картинках 160
Геометрия правильные многогранники Геометрия правильные многогранники 115
Классификация геометрических объектов Классификация геометрических объектов 151
Признаки равенства треугольников Признаки равенства треугольников 131
Симметрия вокруг нас 8 класс Симметрия вокруг нас 8 класс 129
Параллельность двух прямых Параллельность двух прямых 128
Тетраэдр Тетраэдр 132
ПРИЗМА.Сечения призмы ПРИЗМА.Сечения призмы 137
Начертательная геометрия Начертательная геометрия 147
Задачи по аксиомам стереометрии Задачи по аксиомам стереометрии 172
Виды симметрии в геометрии Виды симметрии в геометрии 173
Многогранники. Пирамиды Многогранники. Пирамиды 148
Презентация по геометрии Додекаэдр (10 класс) Презентация по геометрии Додекаэдр (10 класс) 149
Геометрический смысл производной Геометрический смысл производной 130
Презентация по геометрии на тему Векторы (8 класс) Презентация по геометрии на тему Векторы (8 класс) 122
Как измеряются объёмы круглых тел?. Геометрия. 11 класс. Как измеряются объёмы круглых тел?. Геометрия. 11 класс. 119
Презентация по геометрии на тему Подготовка к ЕГЭ. Объём куба,прямоугольного параллелепипеда,призмы Презентация по геометрии на тему Подготовка к ЕГЭ. Объём куба,прямоугольного параллелепипеда,призмы 171
Презентация по теме Параллельность прямых Презентация по теме Параллельность прямых 105
Функция у = х п и ее свойства Функция у = х п и ее свойства 164
Симметрия правильных многогранников Симметрия правильных многогранников 164
Биография Лобачевского Биография Лобачевского 186
Построение сечений тетраэдра и параллелепипеда Построение сечений тетраэдра и параллелепипеда 159
Презентация по математике на тему Приза. Виды призм Презентация по математике на тему Приза. Виды призм 174
Понятие движения Понятие движения 118
Уравнение эллипса Уравнение эллипса 131
Объём призмы 11 класс Объём призмы 11 класс 172