Что такое findtheslide.com?

FindTheSlide.com - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация, доклад по математике на тему Многогранники Параллелепипед

Презентация на тему Презентация по математике на тему Многогранники Параллелепипед, из раздела: Геометрия. Эта презентация содержит 11 слайда(ов). Информативные слайды и изображения помогут Вам заинтересовать аудиторию. Скачать конспект-презентацию на данную тему можно внизу страницы, поделившись ссылкой с помощью социальных кнопок. Также можно добавить наш сайт презентаций в закладки! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них. Все права принадлежат авторам презентаций.

Главная
Геометрия
Презентация по математике на тему Многогранники Параллелепипед

Слайды и текст этой презентации

Слайд 1

Текст слайда:

ГБПОУ КРК «Интеграл» Тема: Многогранники. параллелепипед

Максимович Людмила Викторовна,
преподаватель математики

с. Курсавка
2016год.

Слайд 2

Текст слайда:

Цели:

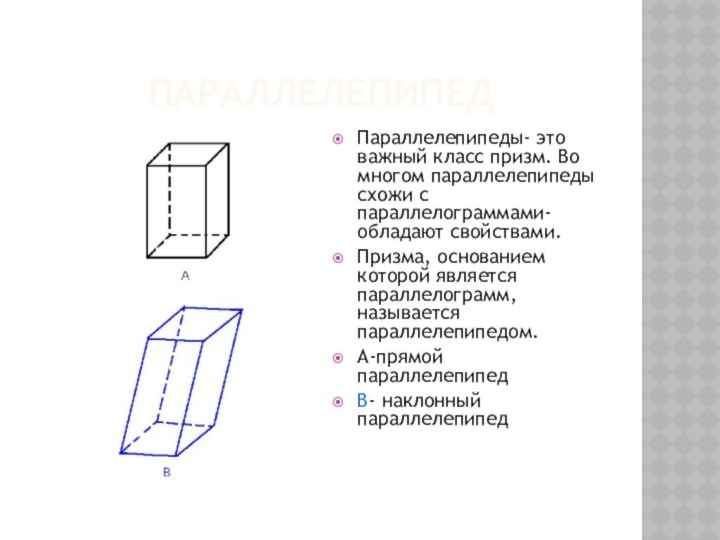
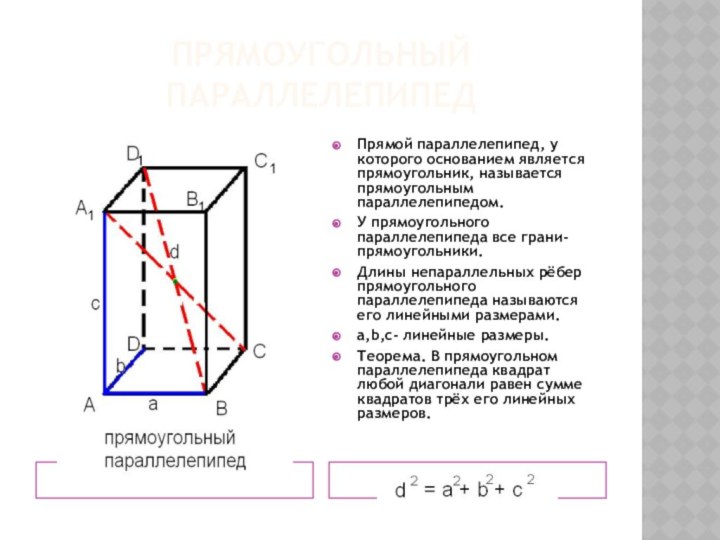
рассмотреть понятие параллелепипеда, прямого параллелепипеда, прямоугольного параллелепипеда ;
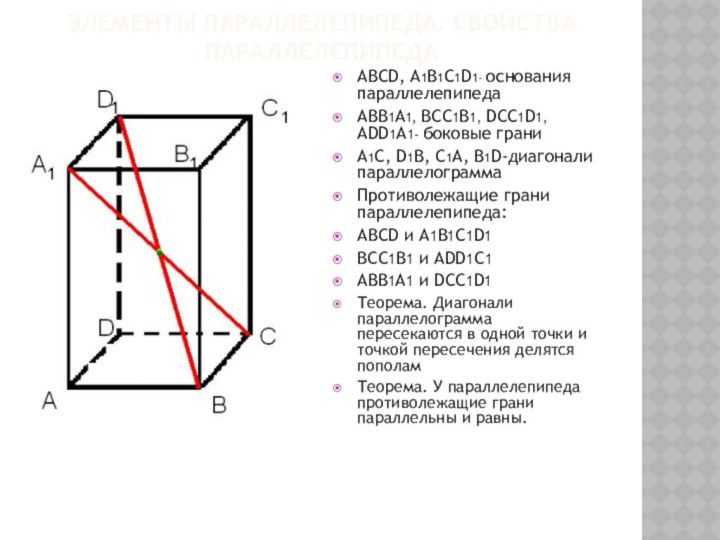
рассмотреть свойства параллелепипеда
ЗАДАЧИ:
развивать логическое мышление;
развивать пространственное воображение;
воспитывать аккуратность при построении чертежей

Слайд 3

Текст слайда:

СОДЕРЖАНИЕ

В презентации указаны виды параллелепипеда, его элементы, свойства. Приведены примеры решения задач.

Слайд 4

Текст слайда:

параллелепипед

Параллелепипеды- это важный класс призм. Во многом параллелепипеды схожи с параллелограммами- обладают свойствами.
Призма, основанием которой является параллелограмм, называется параллелепипедом.
A-прямой параллелепипед
B- наклонный параллелепипед

Слайд 5

Текст слайда:

Элементы параллелепипеда. Свойства параллелепипеда

ABCD, A1B1C1D1- основания параллелепипеда
ABB1A1, BCC1B1, DCC1D1, ADD1A1- боковые грани
A1C, D1B, C1A, B1D-диагонали параллелограмма
Противолежащие грани параллелепипеда:
ABCD и A1B1C1D1
BCC1B1 и ADD1C1
ABB1A1 и DCC1D1
Теорема. Диагонали параллелограмма пересекаются в одной точки и точкой пересечения делятся пополам
Теорема. У параллелепипеда противолежащие грани параллельны и равны.

Слайд 6

Текст слайда:

ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.
У прямоугольного параллелепипеда все грани- прямоугольники.
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами.
a,b,c- линейные размеры.
Теорема. В прямоугольном параллелепипеда квадрат любой диагонали равен сумме квадратов трёх его линейных размеров.

Слайд 7

Текст слайда:

Задача 1

В прямом параллелепипеде стороны оснований 6м и 8 м образуют угол 30º, боковое ребро равно 5м. Найти полную поверхность этого параллелепипеда.

Решение.
Полную поверхность параллелепипеда находим как полную поверхность четырёхугольной призмы высота которой 5м.

Sосн=6·8·sin30º=48·0.5=24(м²)
SБ

Слайд 8

Текст слайда:

Задача 2
Найти диагонали прямоугольного параллелепипеда по трём его линейным размерам:
а)2; 3; 6
б)6; 6; 7

Задача 3
Найти поверхность прямоугольного параллелепипеда по трём его линейным размерам :
10см, 22см, 16см.
(Рассмотреть на модели прямоугольного параллелепипеда)

Слайд 9

Текст слайда:

ВЫВОДЫ

Обучающиеся имеют понятие о параллелепипеде, его элементах, научились строить различные виды параллелепипедов, решать простые задачи.

Слайд 10

Текст слайда:

Источники

Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия.Геометрия.10-11-М.:Просвещение, 2016-255с.
Величко М.В. Математика.9-11 классы: проектная деятельность учащихся; Методическое пособие.- Волгоград; Учитель, 2015.-123с.

Слайд 11