Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Қима тақырыбына есептер шығару (10 сынып)

Содержание

Сабақтың мақсаты: а)Білімділік: Қималар туралы түсінікә) Дамытушылық: Қиюшы жазықтық, көпжақтың қимасы, параллелепипедтің диагональдық қимасы ұғымымен танысуб) Тәрбиелік:Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.
Сабақтың тақырыбы: §9. Қималар Мырзахметова Баян Сабақтың мақсаты: а)Білімділік: Қималар туралы түсінікә) Дамытушылық: Қиюшы жазықтық, көпжақтың қимасы, параллелепипедтің Егер жазықтық пен көпжақтың ортақ бөлігі (үшбұрыш, төртбұрыш, бесбұрыш, т.с.с) көпбұрыш болса, Қиюшы жазықтық тетраэдрдің (параллелепипедтің) жақтарын кесінділер бойымен қиып өтеді. 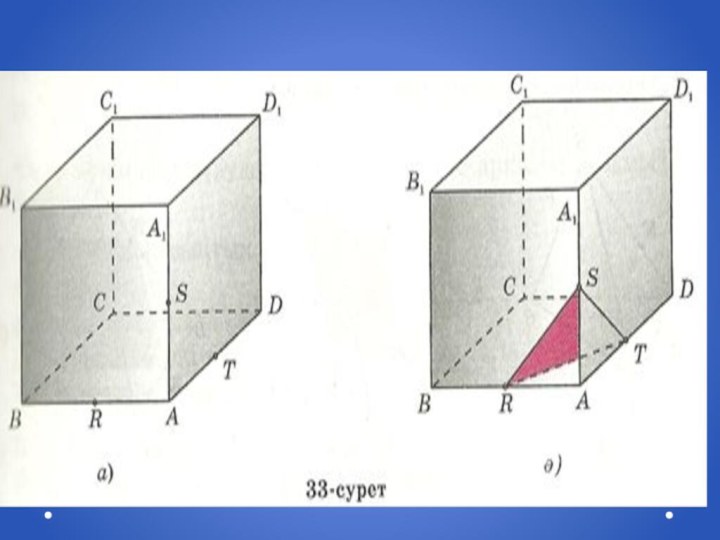Осы кесінділермен жасалған Паралелепипед табандарының параллель диагональдары арқылы өтетін жазықтықпен қимасы оның диагональдық қимасы деп 1-мысал. АВ, АА1, АD қырларының орталары – R,S,T нүктелері арқылы өтетін жазықтықпен АВСDА1В1С1D1 кубының қимасын салыңдар(33,а-сурет) 
Слайды презентации

Слайд 2 Сабақтың мақсаты:
а)Білімділік: Қималар туралы түсінік
ә) Дамытушылық: Қиюшы

Сабақтың мақсаты: а)Білімділік: Қималар туралы түсінікә) Дамытушылық: Қиюшы жазықтық, көпжақтың қимасы,

жазықтық, көпжақтың қимасы, параллелепипедтің диагональдық қимасы ұғымымен танысу
б) Тәрбиелік:Оқушылардың

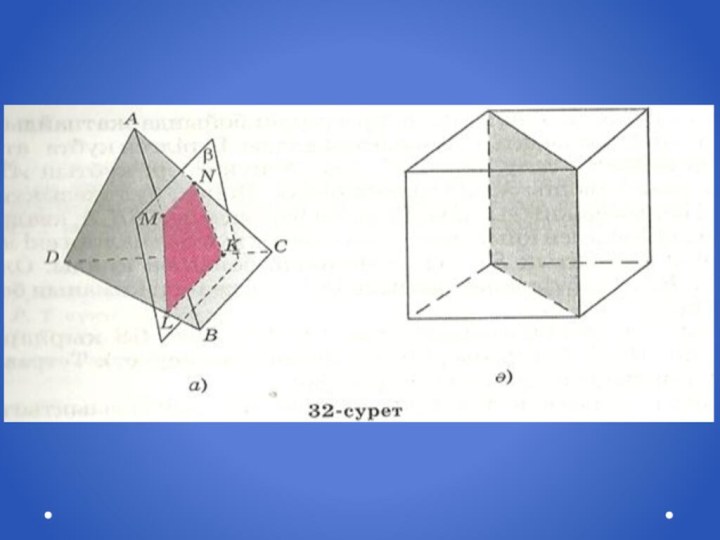
білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Слайд 3 Егер жазықтық пен көпжақтың ортақ бөлігі (үшбұрыш, төртбұрыш,

Егер жазықтық пен көпжақтың ортақ бөлігі (үшбұрыш, төртбұрыш, бесбұрыш, т.с.с) көпбұрыш

бесбұрыш, т.с.с) көпбұрыш болса, онда мұндай жазықтықты қиюшы жазықтық

деп атайды.
32, а-суретте АВСD тетраэдр және β қиюшы жазықтық бейнеленген. А және В нүктелері қиюшы жазықтыққа қатысты әртүрлі жарты кеңістікте жатыр. Тетраэдрдің β жазықтығымен қимасы – LMNK төртбұрышы.

Слайд 4

Слайд 5 Қиюшы жазықтық тетраэдрдің (параллелепипедтің) жақтарын кесінділер бойымен қиып

Қиюшы жазықтық тетраэдрдің (параллелепипедтің) жақтарын кесінділер бойымен қиып өтеді. Осы кесінділермен

өтеді. Осы кесінділермен жасалған көпбұрыш фигураның қимасы болады. Тетраэдрдің

төрт жағы болғандықтан, оның қимасы үшбұрыш немесе төртбұрыш болуы мүмкін. Параллелепипедтің алты жағы бар. Оның қимасы үшбұрыш, төртбұрыш, бесбұрыш және алты бұрыш болуы мүмкін.

Слайд 6 Паралелепипед табандарының параллель диагональдары арқылы өтетін жазықтықпен қимасы

Паралелепипед табандарының параллель диагональдары арқылы өтетін жазықтықпен қимасы оның диагональдық қимасы

оның диагональдық қимасы деп аталады(32,ә-сурет).
Паралелепипедтің қимасын салғанда мынаны есте

ұстау керек, егер қиюшы жазықтық оның қарама-қарсы жақтарын қандай да болмасын кесінділер бойымен қиып өтсе, онда бұл кесінділер өзара параллель болады(9-теорема).

Слайд 7 1-мысал. АВ, АА1, АD қырларының орталары – R,S,T

1-мысал. АВ, АА1, АD қырларының орталары – R,S,T нүктелері арқылы өтетін жазықтықпен АВСDА1В1С1D1 кубының қимасын салыңдар(33,а-сурет) 

нүктелері арқылы өтетін жазықтықпен АВСDА1В1С1D1 кубының қимасын салыңдар(33,а-сурет)
 

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

  • Имя файла: prezentatsiyaҚima-taқyrybyna-esepter-shyғaru-10-synyp.pptx
  • Количество просмотров: 243
  • Количество скачиваний: 5
- Предыдущая Презентация по технологии, изобразительному искусству на тему Дымковская игрушка
Следующая - Презентация Здоровое питание дошкольников

Похожие презентации

Периметр многоугольника 2 класс Периметр многоугольника 2 класс 161
Нанесение размеров. Масштабы Нанесение размеров. Масштабы 139
Замечательные кривые Замечательные кривые 151
Угол между прямой и плоскостью Угол между прямой и плоскостью 136
Презентация по математике на тему : Круги Эйлера. Презентация по математике на тему : Круги Эйлера. 183
Длина окружности (9 класс) Длина окружности (9 класс) 175
Презентация для 9 класса по теме Решение задач по теме Векторы Презентация для 9 класса по теме Решение задач по теме Векторы 144
Признаки равенства треугольников, Геометрия, 7 класс Признаки равенства треугольников, Геометрия, 7 класс 132
Обучение учащихся 7-9 классов решению геометрических задач на построение Обучение учащихся 7-9 классов решению геометрических задач на построение 168
Площади многоугольников Площади многоугольников 130
Презентация по геометрии для 8 класса на тему: Площадь параллелограмма Презентация по геометрии для 8 класса на тему: Площадь параллелограмма 121
Площадь многоугольника Площадь многоугольника 117
Тригонометрические формулы Тригонометрические формулы 192
Вокруг храма с линейкой и циркулем Вокруг храма с линейкой и циркулем 122
Параллелограмм Параллелограмм 121
Теорема Пифагора доказательство Теорема Пифагора доказательство 128
История возникновения геометрии История возникновения геометрии 131
Презентация по математике на тему Обобщающий урок по теме Тела вращения Презентация по математике на тему Обобщающий урок по теме Тела вращения 204
Презентация по геометрии Правильные многогранники (10 класс) Презентация по геометрии Правильные многогранники (10 класс) 133
Введение в стереометрию Введение в стереометрию 191
геометрия геометрия 145
Правильные и полуправильные многогранники Правильные и полуправильные многогранники 126
Виды аксонометрических проекций Виды аксонометрических проекций 124
Внешний угол треугольника Внешний угол треугольника 109
Презентация по геометрии на тему Четырехугольники Презентация по геометрии на тему Четырехугольники 163
Презентация по геометрии на тему Пропорциональные отрезки.Определение подобных треугольников (8 класс) Презентация по геометрии на тему Пропорциональные отрезки.Определение подобных треугольников (8 класс) 344
Самостоятельная работа по геометрии 8 класс Самостоятельная работа по геометрии 8 класс 185
Презентация по геометрии на тему Параллелограмм Презентация по геометрии на тему Параллелограмм 126
Презентация к теме урока: Объемы тел Презентация к теме урока: Объемы тел 132
Построение гиперкуба Построение гиперкуба 141