координат;
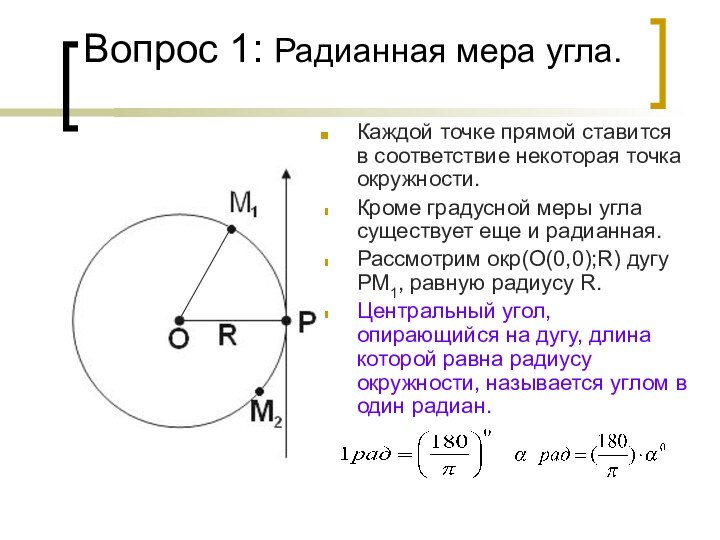
определение синуса, косинуса и тангенса произвольного угла;
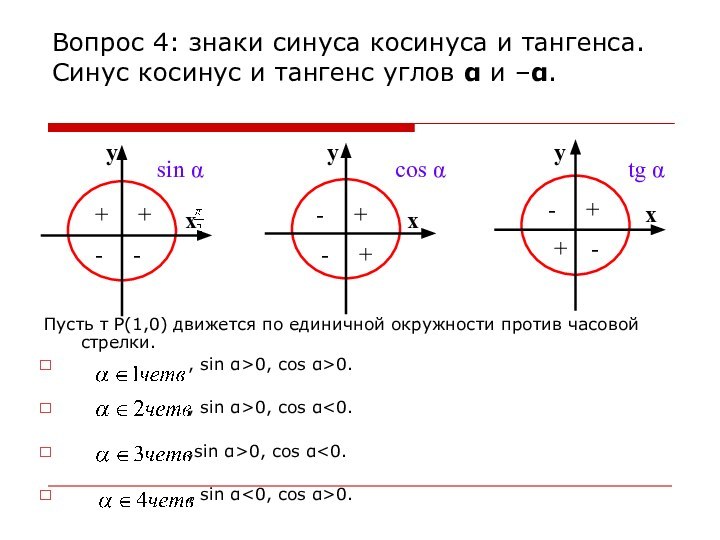
знаки синуса, косинуса
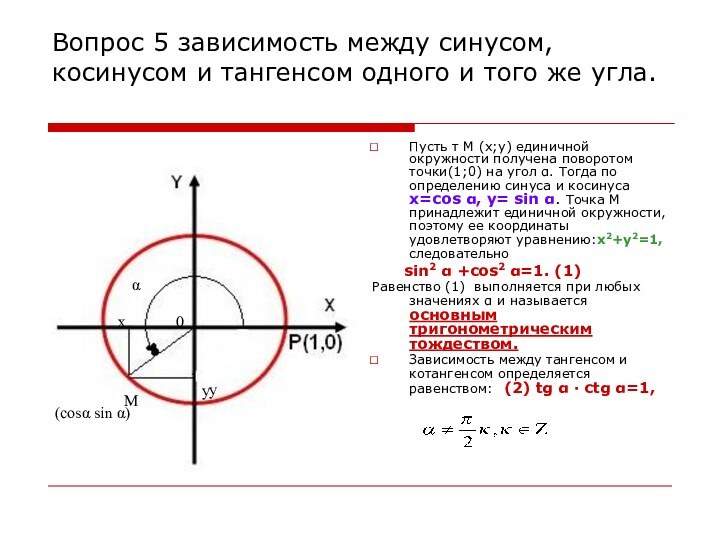
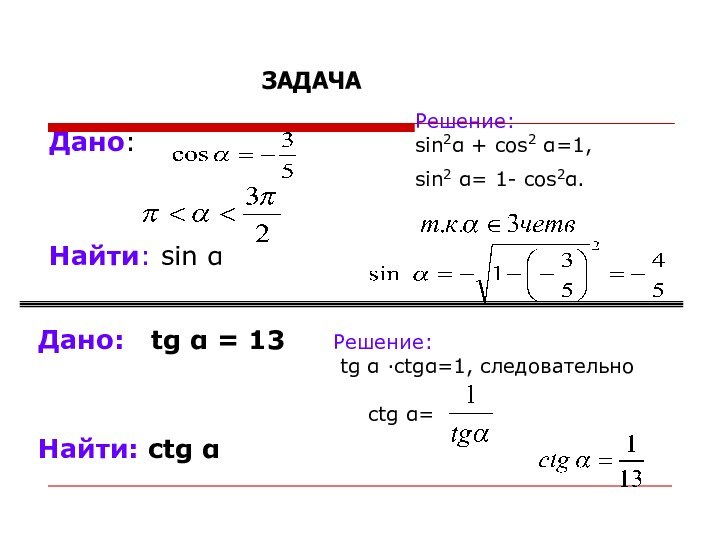
и тангенса;зависимость между синусом, косинусом и тангенсом одного и того же угла;
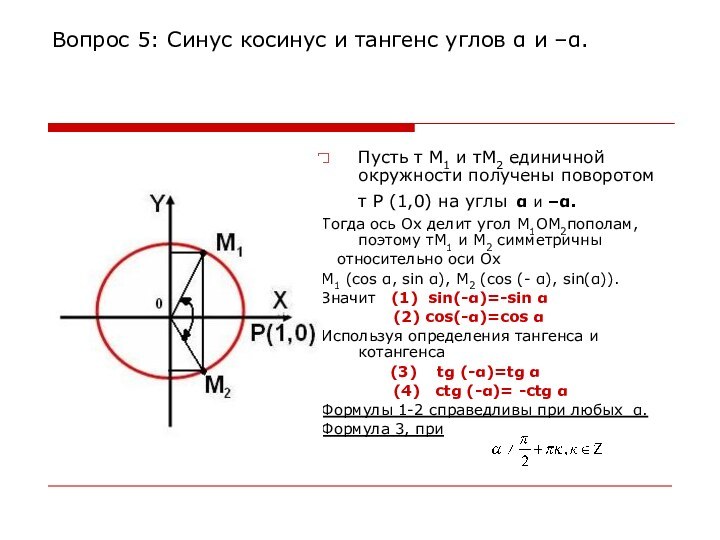
cинус, косинус и тангенс углов α и - α;