Презентация на тему Свойства функции (9 класс)

Слайд 1 Свойства функции

---

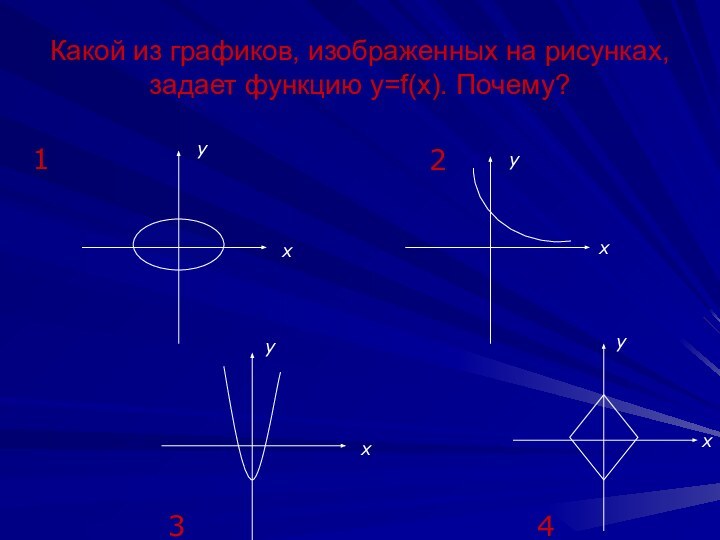
Слайд 2 Какой из графиков, изображенных на рисунках, задает функцию у=f(х). Почему?

1

2

3

4

х

х

х

х

у

у

у

у

---

Слайд 3 Продолжите предложение:
Говорят, что задана функция у=f(х) с областью определения Х,

если даны множество Х и правило f…
Независимая переменная х называется…
Зависимая переменная у называется…
Способы задания функции…

---

Слайд 4 Найдите область определения функции.
а)
б)
в)
г)
д)
е)

---

Слайд 5 Какая из функций, заданных графиками, возрастает (убывает) на промежутке [a;b]

---

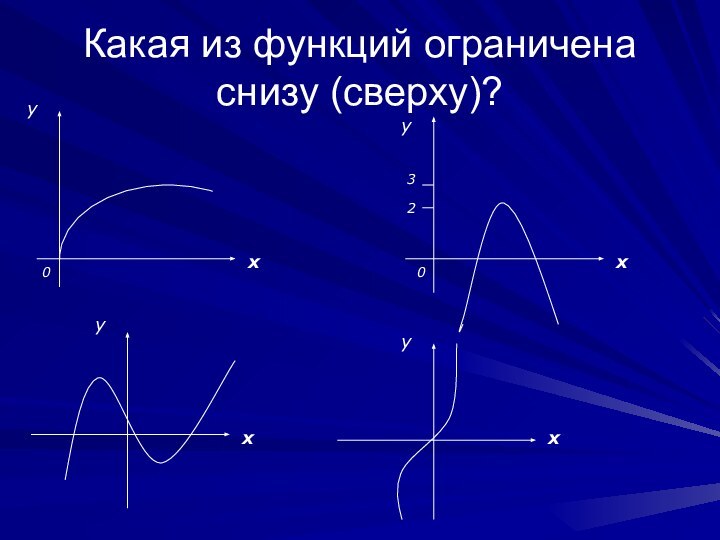
Слайд 6 Какая из функций ограничена снизу (сверху)?
х
х
х
х
у
у
у
у
0
0
2
3

---

Слайд 7 ИЗУЧАЕМ НОВЫЙ МАТЕРИАЛ

---

Слайд 8 Наибольшее и наименьшее значения функции
По графику данной функции найдите наибольшее

и наименьшее значения функции.

х

у

у

2

4

0

1

.

.

[2;1]

на
отрезке

х

---

Слайд 9 Определение 1. Число m называют наименьшим значением функции у=f(х) на множестве

Х, если 1.в Х существует такая точка b, что f(b)=m; 2. для всех х из Х выполняется неравенство f(х) ≥ f(b)

Определение 2.
Число M называют наибольшим значением функции у=f(x) на множестве Х, если
в Х существует такая точка b, что f(b)=M ;
Для всех х и Х выполняется неравенство f(x) ≤ f(b)

---

Слайд 10 ВЫПУКЛОСТЬ ФУНКЦИИ
ФУНКЦИЯ ВЫПУКЛА ВВЕРХ
Х
ФУНКЦИЯ ВЫПУКЛА ВНИЗ
Х
У
У
0
0
.
.
.
.

---

Слайд 11 Четные и нечетные функции
Функцию
у =F(x),х € х
Называют четной,

если для любого значения х из множества х выполняется равенство
F(-x)=F(x)

- Функцию
у = F(x), х € х,
Называют нечетной, если для любого значения х из множества х выполняется равенство
F(-x)=-F(x)

---

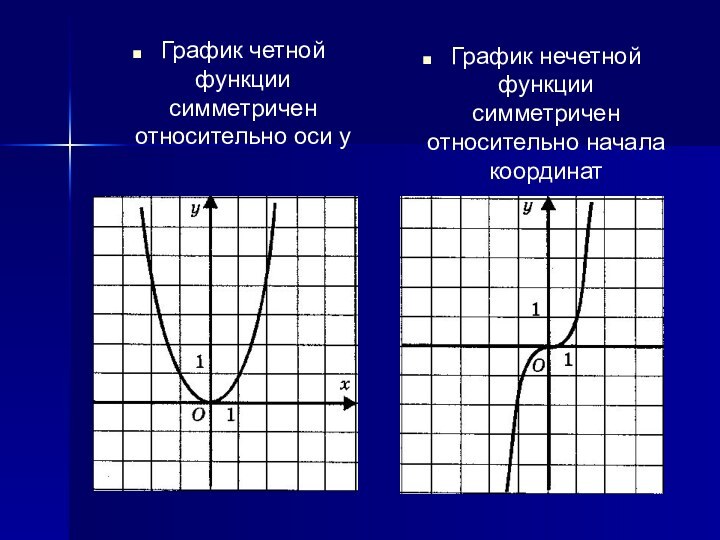
Слайд 12 График четной функции симметричен относительно оси у

График нечетной функции симметричен относительно начала координат

---

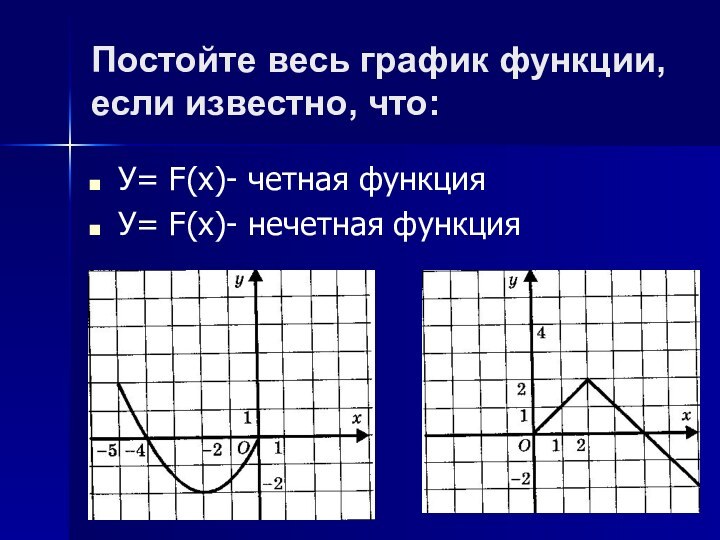
Слайд 13 Постойте весь график функции, если известно, что:
У= F(x)- четная функция
У=

F(x)- нечетная функция

---

Слайд 14 На каком рисунке изображен график непрерывной функции на отрезке[a, b]
.
.
.
.
.
.
2

1

---

Слайд 15 Свойства функции
Область определения
Монотонность (промежутки возрастания и убывания функции)
Ограниченность
Наименьшее и наибольшее

значения функции
Непрерывность функции
Область значений
Выпуклость
Четность и нечетность функции

---

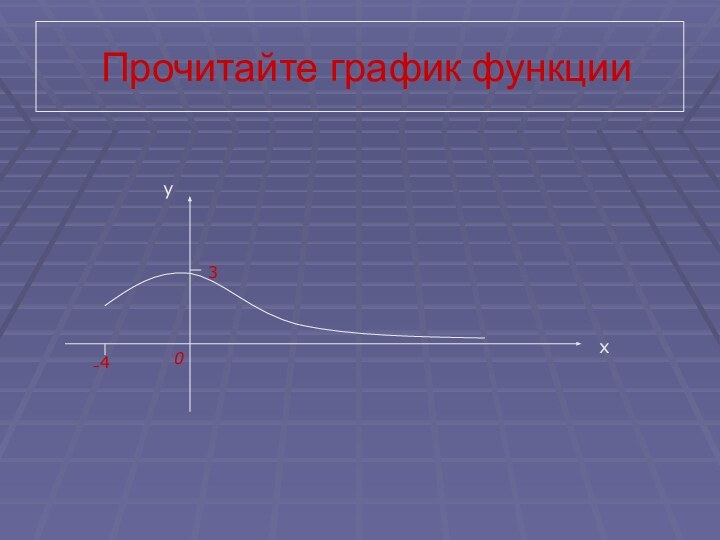
Слайд 16 Прочитайте график функции
х
у
0
3
4

---

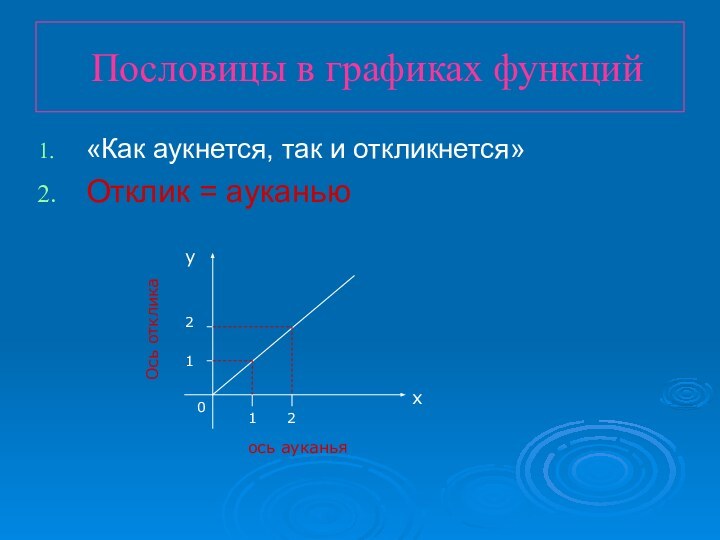
Слайд 17 Пословицы в графиках функций
«Как аукнется, так и откликнется»
Отклик = ауканью
1
1
2
2
0
х
у
ось

ауканья

Ось отклика

---

Слайд 18 ИЗОБРАЗИТЕ ГРАФИЧЕСКИ ПОСЛОВИЦЫ
«Чем дальше в лес, тем больше дров»
«Выше

меры конь не скачет»
«Ни кола, ни двора»

---